数值分析：Python实现高斯赛德尔迭代法（Gauss-Seidel）与雅可比迭代法（Jacobi）_如何对比高斯迭代，雅各比迭代的收敛速度

Python实现高斯赛德尔迭代法（Gauss-Seidel）与雅可比迭代法（Jacobi）

数值分析：Python实现高斯赛德尔迭代法（Gauss-Seidel）与雅可比迭代法（Jacobi）

一、基本迭代法

二、雅可比迭代法（Jacobi）

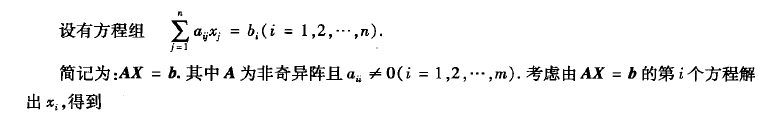
三、高斯—赛德尔迭代法（Gauss-Seidel）

题目：分别使用雅可比迭代法与高斯—赛德尔迭代法求解Ax=b线性方程组，其中A为10阶希尔伯特矩阵输出解向量与迭代次数。

希尔伯特矩阵 Hilbert matrix

希尔伯特矩阵（Hilbert matrix），矩阵的一种，其元素A（i,j）=1/(i+j-1)，i,j分别为其行标和列标。

代码实现：

import numpy as np
n=10
def Jacobi(A,b,x0,xstar):
    k=0
    while True:
        for i in range(0, n):
            sum = 0.0
            for j in range(0, i):
                sum = sum + A[i][j] * x0[j]
            for j in range(i + 1, n):
                sum = sum + A[i][j] * x0[j]
            xstar[i] = (b[i] - sum) / A[i][i]
        temp = np.fabs(xstar[0] - x0[0])
        for j in range(1, n):
            if np.fabs(xstar[j] - x0[j]) > temp:
                temp = np.fabs(xstar[j] - x0[j])
        for j in range(0, n):
            x0[j] = xstar[j]
        k = k + 1
        if (temp < 1.0e-6 or k > 1000) :
            break
    print("Jacobi:",k)

def Gauss(A,b,x0,xstar):
    k = 0
    while True:
        for i in range(0, n):
            sum = 0.0
            for j in range(0, i):
                sum = sum + A[i][j] * xstar[j]
            for j in range(i + 1, n):
                sum = sum + A[i][j] * x0[j]
            xstar[i] = (b[i] - sum) / A[i][i]
        temp = np.fabs(xstar[0] - x0[0])
        for j in range(1, n):
            if np.fabs(xstar[j] - x0[j]) > temp:
                temp = np.fabs(xstar[j] - x0[j])
        for j in range(0, n):
            x0[j] = xstar[j]
        k = k + 1
        if (temp < 1.0e-6 or k > 1000) :
            break
    print("Gauss:",k)

def main():
    A=np.zeros([n,n],float)
    b=np.zeros(n,float)
    x0=np.zeros(n,float)
    Jex = np.zeros(n,float)
    GSex = np.zeros(n,float)
    for i in range(0,n):
        for j in range(0,n):
            A[i][j] = 1./(i+1+j)
    for i in range(0,n):
        A[i][i] = A[i][i] + 0.5
        b[i] = 1
        x0[i] = 0

    Jacobi(A,b,x0,Jex)
    for i in range(0,n):
        x0[i] = 0
    Gauss(A,b,x0,GSex)
    for i in range(0,n):
        print("Jex[",i,"]=",Jex[i])
    print("\n")
    for i in range(0,n):
        print("GSex[",i,"]=",GSex[i])

if __name__ == '__main__':
main()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

通过编码计算，对比两种算法的收敛速度与结果。可以看出，高斯赛德
尔迭代法的收敛速度比雅可比迭代法收敛速度要快的多。