c++多边形扫描线填充算法_【基础算法】获取多边形内全部整数点（polygon to mask）算法——扫描线算法...

代码已开源：https://github.com/thisiszhou/polygon2mask （Python）

最近写实例分割代码时再次遇到了polygon转化为mask的需求，在二维平面中，快速得到多边形内部的全部点，看似简单。但是同时适配凸凹多边形的情况下，又追求一定的速度，还是有不少细节需要打磨，本文采用扫描线算法解决该问题。

上述代码是笔者第三次写扫描线算法，还是有不少卡壳的地方，在此记录一下该算法思路。如果并不关心算法实现细节，可以直接阅读算法功能与接口介绍。

测试后速率不如opencv内置函数快，opencv内置函数调用与速率对比参见算法速率测试。

一、算法功能与接口介绍

入参：

1. image_size：一张图片的尺寸（H，W）；
2. polygon：多边形顶点坐标
   ；
3. exist_mask：是否已有mask，默认为None。

输出：

0、1 mask矩阵，多边形内部点为1，否则为0（如图一右）

注：

1. polygon顶点坐标支持浮点数；
2. 若边界点正好为整数格点，被认作为多边形内部点；
3. 支持凸凹多边形、自相交多边形；
4. 若多边形不只一个，入参中还有一个参数exist_mask，可以使用for循环调用此算法接口，将之前生成的mask继续再传进来，算法会在现有mask的基础上，扫描下一个多边形内部点；
5. 扫描出的是空间离散化后的内部整数格点。

二、算法原理

扫描线采取水平方向与垂直方向，后续处理会有很大的不同，本文算法采用水平线。

• 核心算法思路：扫描线

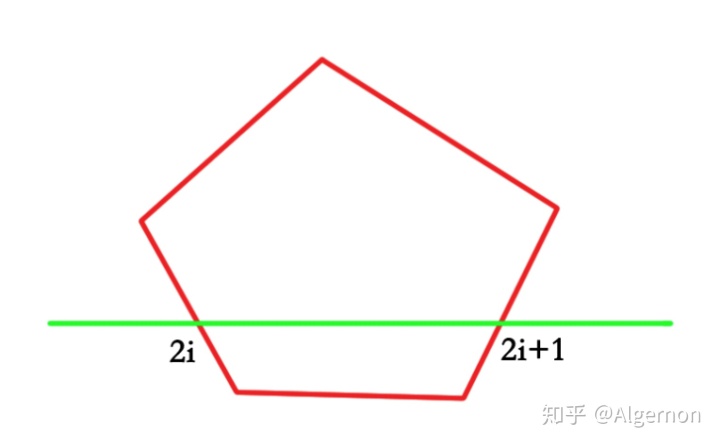
如上图所示，使用一条水平线与多边形相交，若多边形为封闭多边形，则必有