- 1从三份白皮书看汽车网络安全模型_idprr
- 2【笔记】1、初学python3网络爬虫——环境配置_cmd加入python 爬虫
- 3vue封装一个卡片组件_vue card
- 4java基础(类,对象)_attributeerror: module 'scrapy' has no attribute '
- 5最常见DDOS攻击工具有哪些?怎么防御DDOS攻击?
- 6[ 云计算 | Azure 实践 ] 在 Azure 门户中创建 VM 虚拟机并进行验证
- 7面试必备:分库分表经典15连问_分库分表面试题
- 8【愚公系列】2023年11月 Java教学课程 203-RabbitMQ(SpringAMQP)
- 9网络安全(黑客)——2024自学
- 10ROS的卸载与安装【血泪总结!亲测有效】_卸载ros
机器人学matlab建模实例,中正平和的机器人学笔记——3.几个MATLAB实例
赞
踩
0. 轨迹
学机器人学前最想知道的,就是如何把机器人末端执行器平滑地从A点移动到B点,也许不太准确,应当说从位姿A移动到位姿B。
0.1 关节空间运动
考虑末端执行器在以下两个笛卡尔位姿之间移动
下面两种语法都可以表示(x,y,z,θ)的位姿
mdl_puma560 %载入提供的puma560机械臂模型
T1 = transl(0.4, 0.2, 0) * trotx(pi);
%T1 = SE3(0.4, 0.2, 0) * SE3.Rx(pi);
T2 = transl(0.4, -0.2, 0) * trotx(pi/2);
%T2 = SE3(0.4, -0.2 0) * SE3.Rx(pi/2);
那么与之对应的关节坐标就是
q1 = p560.ikine6s(T1);
q2 = p560.ikine6s(T2);
我们再给出时间向量
t = [0:0.05:2]';
通过对q1和q2两个位姿之间进行平滑插值就可以得到一个关节空间轨迹,我们用如下函数
q = jtraj(q1, q2, qt);
%jtraj相当于具有tpoly插值的mtraj,
%但优化了多轴情况,且允许使用额外参数设置v0和vt
%以后就不用下面两个插值函数
%q = mtraj(@tpoly, q1, q2, t);
%q = mtraj(@lspb, q1, q2, t);
%[q,qd,qdd] = jtraj(q1, q2, t);
%以下是SerialLink类提供的jtraj更简便的用法
q = p560.jtraj(T1, T2, t);
最终得到的轨迹可以绘制出来观察,包括关节角的变化都可以看到
p560.plot(q) %绘制关节角的变化如图a
plot(t, q) %绘制关节角随时间的变化,如图a
T = p560.fkine(q); %得到三位笛卡尔轨迹
p = transl(T);%轨迹的位移部分
% plot(p(:,1),p(:,2)) %绘制xy平面内的轨迹,如图c
% plot(t, tr2rpy(T)) %画出另一种位姿表达,如图d
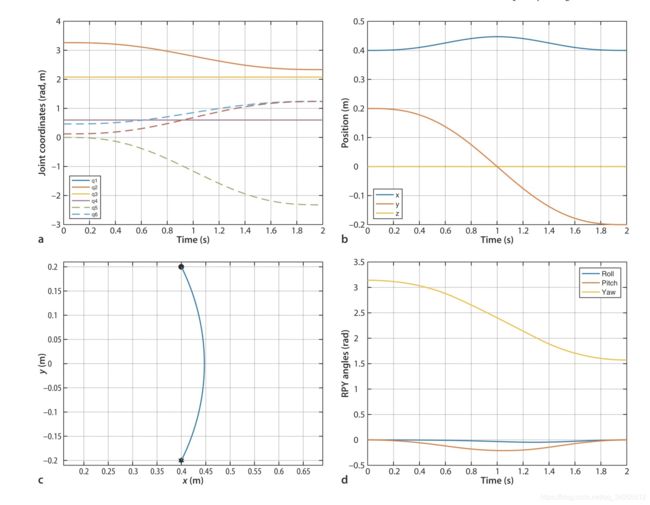
从图c可以看到,显然我们做的这条轨迹不是一条直线。这个很好理解,我们只给机器人初始点和结束点两个坐标,那么机器人在运动时,转动其腰部关节,显然会是一个弧线。那么我们如何保证机器人末端在笛卡尔空间中也划出一条直线轨迹呢?
其实很简单,将原来的jtraj函数换成ctraj就可以,当然这里的简单只得是用MATLAB仿真起来很简单,并不是其他的。
Ts = ctraj(T1, T2, length(t));
%plot(t, transl(Ts) )
%plot(t, tr2rpy(Ts) )
qc = p560.ikine6s(Ts);
plot(t,q)
p560.plot(qc)
- #include<Eigen/Dense>#include
usingnamespaceEigen;usingnamespacestd;intmain(){ MatrixXdK(2,2); K<<4,5,8,5; cou... [详细] 赞
踩
- 1、频域滤波的基本步骤:1)、使用函数paddedsize获取填充函数;PQ=paddedsize(size(f));2)、得到使用填充的傅里叶变换,F=fft2(f,PQ(1),PQ(2));3)、获取滤波函数H(高通、低通等);4)、将... [详细]
赞
踩
- matlab对三种高通滤波器(理想高通巴特沃斯高通高斯高通)及拉普拉斯增强算子自写算法实现及比较在时域中分析_常见的三种高通滤波器常见的三种高通滤波器三种高通滤波器(理想高通巴特沃斯高通高斯高通)及拉普拉斯增强算子的时域图像1、理想高通滤波... [详细]
赞
踩
- MATLAN支持向量机(SVM)详解——含代码_matlabsvmmatlabsvmMATLAB支持向量机(SVM)详细解释(含代码)基础线性可分最大间隔超平面SVM分类基本代码和工具二分类线性非线性多分类详细解释基础线性可分简单来讲就是如... [详细]
赞
踩
- 式中,x为海杂波幅度瞬时值,二迂为杂波幅度的均方值。这里假定海杂波是由许多相互独立的随机散射体形成的,因此根据中心极限定理,其功率服从于正态分布,其包络的概率密度函数为瑞利分布,这种分布适合于低分辨率雷达(天线波束宽度大于二,脉冲宽度大于1... [详细]
赞
踩
- %【例8-7】利用randan函数产生高斯分布序列。%【例8-8】利用rand函数产生服从(a-b)均匀分布的随机序列。%【例8-9】服从指数分布的热噪声随机序列的实现。%【例8-10】产生瑞利分布的热噪声。%【例8-7】利用randan函... [详细]
赞
踩
- 瑞利信道的产生主要有两种方法:正弦波叠加法和成型滤波法。MATLAB自带了rayleighchan函数来产生时变瑞利信道,据说用的是Jakes频域反变换方法来产生时间相关性的瑞利模型。【见博客】%Tsthesampletimeofinput... [详细]
赞
踩
- rayleighchan实现瑞利多径衰落信道1.命令格式:chan=rayleighchan(ts,fd,tau,pdb)其中:ts—为输入信号的采样周期,fd—就是Doppler频偏,以Hz为单位,与速率的换算关系为v×fc/c,fc是载... [详细]
赞
踩
- 2.6(1)产生均匀分布的随机数x~U(0,1);(2)产生服从2σ=4的瑞利分布的随机数y;分析:y的分布函数:821)(yYeyF--=其反函数为)1ln(8)(1xxFY--=-令)1ln(8)(1xxFyY--==-,此处有x~U(... [详细]
赞
踩
- 如何用matlab生成随机数函数1.MATLAB函数rand产生在区间(0,1)的均匀随机数,它是平均分布在(0,1)之间。一个称为seed的值则是用来控制产生随机数的次数。均匀随机数函数的语法为rand(n),rand(m,n),其结果分... [详细]
赞
踩
- 目录a.基本随机数1.rand()2.randn()b.连续型分布随机数3.unifrnd()4.normrnd()5.chi2rnd()6.frnd()7.trnd()8.betarnd()10.gamrnd()11.lognrnd()1... [详细]
赞
踩
- 热噪声信号的产生在我们仿真雷达信号处理流程时,需要先仿真雷达的回波信号,同时为了更符合实际情况,我们还需要给雷达回波信号叠加上噪声或杂波。但由于噪声和杂波并不是确知信号,所以通过统计特性来分析,需要用到概率论的方法。在数学上,用概率密度函数... [详细]
赞
踩
- 实验一瑞利信道的仿真一引言:瑞利信道介绍瑞利衰落信道(Rayleighfadingchannel)是一种无线电信号传播环境的统计模型。这种模型假设信号通过无线信道之后,其信号幅度是随机的,即“衰落”,并且其包络服从瑞利分布。[1]瑞利分布就... [详细]
赞
踩
- 2019独角兽企业重金招聘Python工程师标准>>>..._matlab实现高斯分布与均匀分布的转换matlab实现高斯分布与均匀分布的转换2019独角兽企业重金招聘Python工程师标准>>>matlab中rand和r... [详细]
赞
踩
- 该程序复现《AModifiedBinaryPSOtosolvetheThermalUnitCommitmentProblem》,主要做的是一个考虑需求响应的机组组合问题,首先构建了机组组合问题的基本模型,在此基础上,进一步考虑负荷侧管理,也... [详细]
赞
踩
- 创建预定义的二维滤波器matlab创建预定义的二维滤波器目录一、概述1、算法概述2、主要函数二、创建各种滤波器并对图像进行滤波1、示例代码2、计算结果三、参数解析输入参数输出参数五、参考链接... [详细]
赞
踩
- clc;clearall;closeall;%Top-Hat测试图像I=im2double(imread('D:\GrayFiles\9-40.tif'));%=========================灰度Top-Hat操作====... [详细]
赞
踩
- ima=double(imread('data/house.png'));ima=double(rgb2gray(uint8(ima)));特别注意在在使用rgb2gray这个函数将3通道转化成单通道的时候,必须先将这个图像转化成uint8... [详细]
赞
踩
- 所以可以用如下步骤来解决:递归定义最优解计算公式构造dp矩阵,按照公式逐步计算。接下来我们分别在最长公共子串、最长公共子序列和01背包问题中演示如何应用上面的套路..._最长公共子序列matlab最长公共子序列matlab适合动态规划(DP... [详细]
赞
踩
- 2.看一下MATLAB里的premnmx函数和postmnmx函数.它们一个是归一一个是反归一3.并不是归一化的数据训练效果就好神经网络训练的时候,应该考虑极值情况,即归一化的时候要考虑你所需要识别参数的极值,以极值作分母,这样可能效果更好... [详细]
赞
踩


