编辑这个页面须要登录或更高权限!
- 您刚才的请求只有这个用户组的用户才能使用:自动确认用户
- 如果您还没有登录请登录后重试。编程那点事是一个开放式网站,修改本站大部分内容仅须要花10秒钟时间创建一个账户。 如果您已经登录,本页面可能是受保护的内容。如果您认为有修改的必要,请联系本站管理人员。
- 该页面已被锁定以防止编辑。
C++ 按位运算符
在本教程中,我们将借助示例学习C ++中的按位运算符。
在C ++中,按位运算符对单个位级别的整数数据执行运算。这些操作包括测试,设置或移位实际位。例如,
a & b; a | b;
这是C ++中包含的6个按位运算符的列表。
| 运算符 | 名称 | 描述 | 实例 |
|---|---|---|---|
| & | 按位与 | 如果同时存在于两个操作数中,二进制 AND 运算符复制一位到结果中。 | (A & B) 将得到 12,即为 0000 1100 |
| | | 按位或 | 如果存在于任一操作数中,二进制 OR 运算符复制一位到结果中。 | (A | B) 将得到 61,即为 0011 1101 |
| ^ | 按位异或 | 如果存在于其中一个操作数中但不同时存在于两个操作数中,二进制异或运算符复制一位到结果中。 | (A ^ B) 将得到 49,即为 0011 0001 |
| ~ | 按位补码 | 二进制补码运算符是一元运算符,具有"翻转"位效果,即0变成1,1变成0。 | (~A ) 将得到 -61,即为 1100 0011,一个有符号二进制数的补码形式。 |
| << | 左移 | 二进制左移运算符。左操作数的值向左移动右操作数指定的位数。 | A << 2 将得到 240,即为 1111 0000 |
| >> | 右移 | 二进制右移运算符。左操作数的值向右移动右操作数指定的位数。 | A >> 2 将得到 15,即为 0000 1111 |
这些运算符是必需的,因为计算机CPU中的算术逻辑单元(ALU)在位级执行算术运算。
注意:按位运算符只能与 char 和 int数据类型一起使用。
1. C ++按位与(&)运算符
当且仅当两个操作数均为1时,按位AND&运算符才返回1。否则,它将返回0。
下表演示了按位AND运算符的工作方式。 假设a和b是两个只能取二进制值即1和0的操作数。
| a | b | a & b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
注意:上表被按位AND运算符称为“真值表”。
让我们看一下两个整数12和25的按位与运算:
12 = 00001100 (二进制) 25 = 00011001 (二进制) //12和25的按位与运算 00001100 & 00011001 _________ 00001000 = 8 (十进制)
示例1:按位与(&)
#include <iostream>
using namespace std;
int main() {
//声明变量
int a = 12, b = 25;
cout << "a = " << a << endl;
cout << "b = " << b << endl;
cout << "a & b = " << (a & b) << endl;
return 0;
}输出结果
a = 12 b = 25 a & b = 8
在上面的示例中,我们声明了两个变量a和b。在这里,请注意这行,
cout << "a & b = " << (a & b) << endl;
在这里,我们在变量a和b之间执行按位与(&)操作。
2. C ++按位或(|)运算符
如果至少有一个操作数为1,则按位或(|)运算符返回1。否则返回0。
下面的真值表演示了按位OR运算符的工作方式。假设a和b为两个只能取二进制值(即1或0)的操作数。
| a | b | a | b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
让我们看一下两个整数12和25的按位或运算:
12 = 00001100 (二进制) 25 = 00011001 (二进制) //12和25的按位或运算 00001100 | 00011001 _________ 00011101 = 29 (十进制)
示例2:按位或(|)运算符
#include <iostream>
int main() {
int a = 12, b = 25;
cout << "a = " << a << endl;
cout << "b = " << b << endl;
cout << "a | b = " << (a | b) << endl;
return 0;
}输出结果
a = 12 b = 25 a | b = 29
在按位或中a = 12和b = 25得出29。
3. C ++按位异或(^)运算符
当且仅当其中一个操作数为1时,按位XOR ^运算符才返回1。但是,如果两个操作数均为0,或者两个都为1,则结果为0。
下面的真值表演示了按位OR运算符的工作方式。假设a和b为两个只能取二进制值(即1或0)的操作数。
| a | b | a ^ b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
让我们看一下两个整数12和25的按位XOR运算:
12 = 00001100 (二进制) 25 = 00011001 (二进制) //12和25的位异或运算 00001100 ^ 00011001 _________ 00010101 = 21 (十进制)
示例3:按位异或(^)运算符
#include <iostream>
int main() {
int a = 12, b = 25;
cout << "a = " << a << endl;
cout << "b = " << b << endl;
cout << "a ^ b = " << (a ^ b) << endl;
return 0;
}输出结果
a = 12 b = 25 a ^ b = 21
a = 12和b = 25的按位异或运算得到21。
4. C ++按位补码运算符
按位补码运算符是一元运算符(仅在一个操作数上起作用)。 用~表示,将二进制数字1更改为0,将0更改为1。
需要注意的是,任何整数N的位补码等于 -(N+1)。例如
例如整数35。按照规则,35的按位补码应为-(35 +1)= -36。现在,让我们看看是否得到正确的答案。
35 = 00100011 (二进制) // 使用按位补码运算符 ~ 00100011 __________ 11011100
在上面的示例中,我们得出00100011(35)的按位补码为11011100。在这里,如果将结果转换为十进制,则得到220。
但是,需要注意的是,我们不能直接将结果转换为十进制,从而获得所需的输出。这是因为二进制结果11011100也相当于-36。
为了理解这一点,我们首先需要计算-36的二进制输出。我们使用2的补数来计算负整数的二进制数。
2的补码
在二进制算术中,1的补码将0更改为1,将1更改为0。 而且,如果我们在1的补码结果上加1,我们就会得到原始数字的2的补码。
例如,
36 = 00100100 (二进制) 1的补码 = 11011011 2的补码 : 11011011 + 1 _________ 11011100
在这里,我们可以看到36的2的补码(即-36)是11011100。 该值相当于35的按位补码。
因此,我们可以说35的位补码是-36。
示例4:按位补码
#include <iostream>
int main() {
int num1 = 35;
int num2 = -150;
cout << "~(" << num1 << ") = " << (~num1) << endl;
cout << "~(" << num2 << ") = " << (~num2) << endl;
return 0;
}输出结果
~(35) = -36 ~(-150) = 149
在上面的示例中,我们声明了两个整数变量num1和num2,并分别用值35和-150初始化它们。
然后我们分别用代码(~num1)和(~num2)计算它们的位补码,并将它们显示在屏幕上。
35的按位补码 = - (35 + 1) = -36 即 ~35 = -36 -150的按位补码 = - (-150 + 1) = - (-149) = 149 即 ~(-150) = 149
这正是我们在输出中得到的。
C ++移位运算符
C ++编程中有两个移位运算符:
右移运算符 >>
左移运算符 <<
1、C ++右移运算符(>>)
右移运算符将所有位向右移一定数量的指定位。用>>表示。
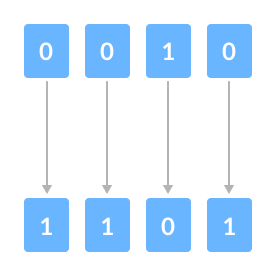
当我们向右移动任何数字时,最低有效位将被丢弃,而最高有效位将被零替换。
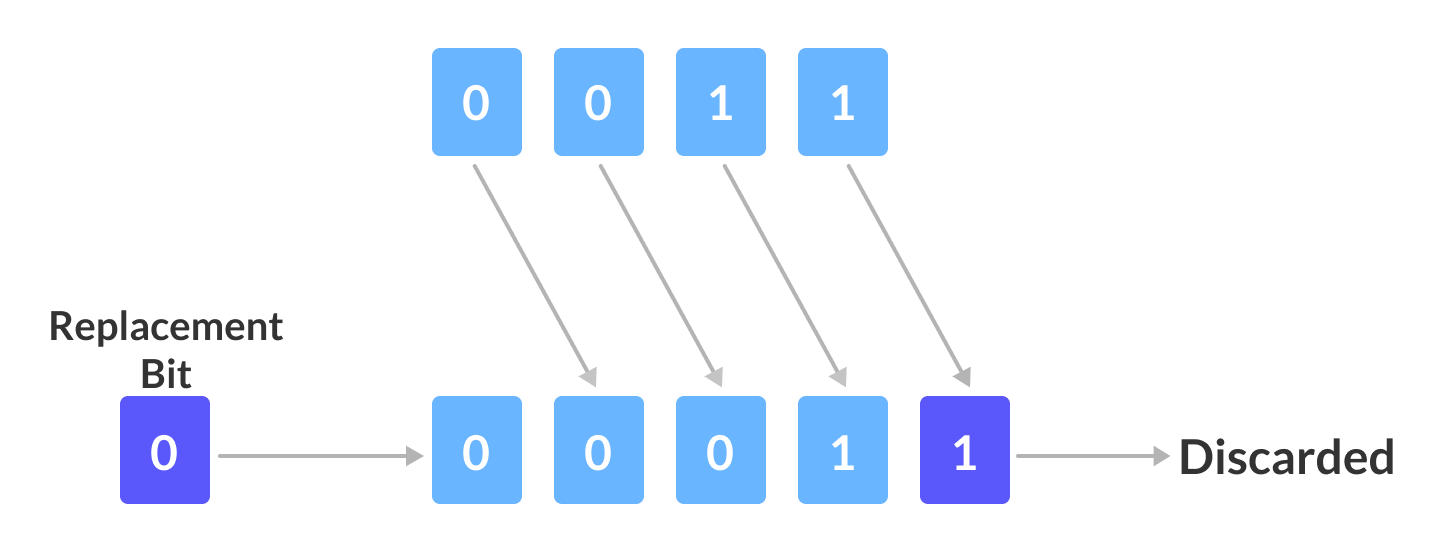
从上图可以看到,我们有一个4位数字。当我们对其执行一位右移操作时,每个单独的位向右移1位。
结果,最右边的位被丢弃(Discarded),而最左边的位保持为空。此空位由0代替(Replacement Bit)。
2、C ++左移运算符
左移位运算符将所有位向左移位一定数量的指定位。用<<表示。
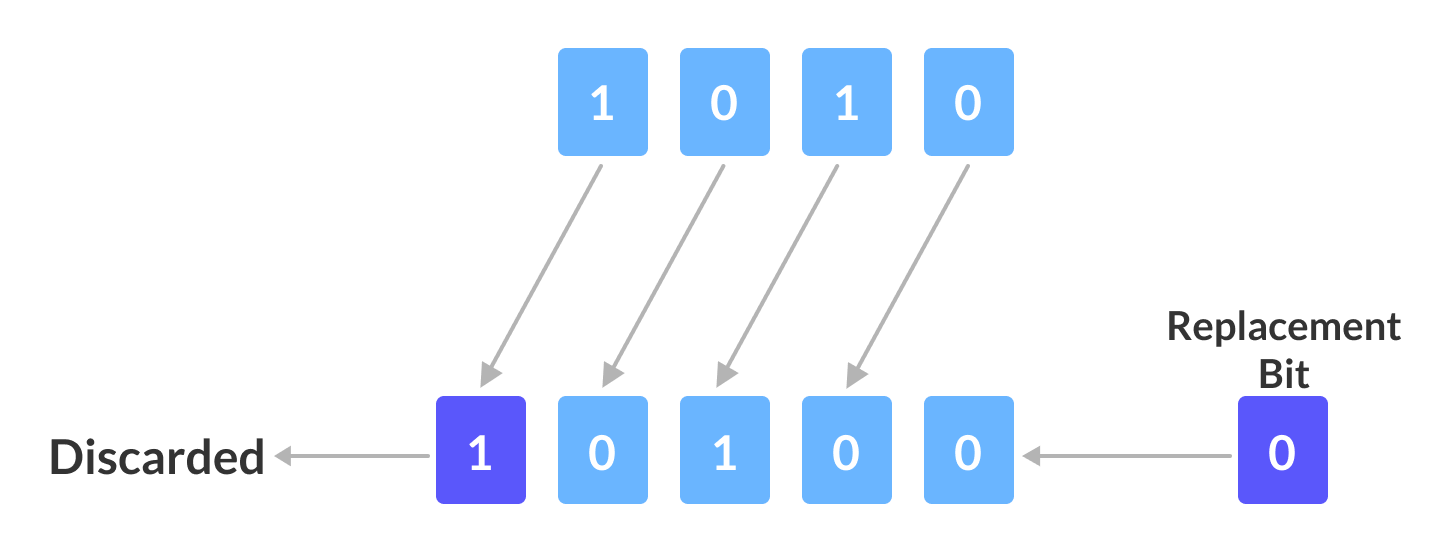
从上图可以看到,我们有一个4位数字。当我们对其执行1位左移操作时,每个单独的位向左移1位。
结果,最左边的位被丢弃(Discarded),而最右边的位保持为空。此空位由0代替(Replacement Bit)。
示例5:移位运算符
#include <iostream>
int main() {
//声明两个整数变量
int num = 212, i;
//右移操作
cout << "右移:" << endl;
//使用for循环将num从0位右移到3位
for (i = 0; i < 4; i++) {
cout << "212 >> " << i << " = " << (212 >> i) << endl;
}
//左移操作
cout << "\n左移:" << endl;
//使用for循环将num从0位左移到3位
for (i = 0; i < 4; i++) {
cout << "212 << " << i << " = " << (212 << i) << endl;
}
return 0;
}输出结果
右移: 212 >> 0 = 212 212 >> 1 = 106 212 >> 2 = 53 212 >> 3 = 26 左移: 212 << 0 = 212 212 << 1 = 424 212 << 2 = 848 212 << 3 = 1696
从上面程序的输出,我们可以推断出,对于任何数字N,右移运算符的结果都是:
N >> 0 = N N >> 1 = (N >> 0) / 2 N >> 2 = (N >> 1) / 2 N >> 3 = (N >> 2) / 2
等等。
同样,左移运算符的结果为:
N << 0 = N N << 1 = (N << 0) * 2 N << 2 = (N << 1) * 2 N << 3 = (N << 2) * 2
等等。
因此,我们可以得出结论,
N >> m = [ N >> (m-1) ] / 2 N << m = [ N << (m-1) ] * 2
- Copyright © 2003-2013 菜鸟教程。
- 版权与免责声明
