采用广度优先的策略，依次生成所有子节点。
① 设计一个限界函数，计算各节点的值，把符合限界条件的节点放入活节点表HT中。使用队列或优先队列，先进先出。
当可行解不止一个时，为衡量这些可行解的优劣，需要通过目标函数来进行评价。
② 对于待处理的节点，根据限界函数估算目标函数的可能取值，从中选取使目标函数取得极值（极大或极小）的节点进行广度优先搜索。
也就是说，每次都选择“最有利”的一个子节点作为优先扩展节点，一次性将这个节点的子节点全部展开，然后继续根据步骤①②对新展开的子节点进行选取。
③ 使搜索朝着解空间树上有最优解的方向前进，由此尽快找到问题的解。

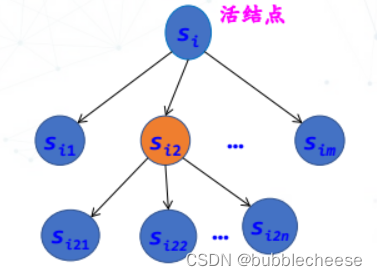
分支限界法节点展开图

1.3 分枝限界法与回溯法的异同

相同点：都在问题的解空间树中搜索问题的解
不同点：

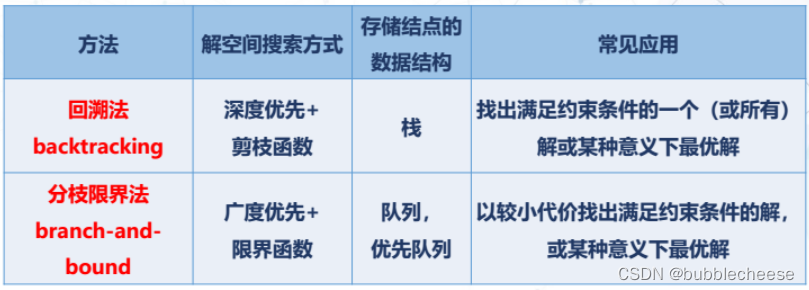
2 设计步骤

确定解空间结构：定义问题的解空间，确定易于搜索的解空间结构。
设计限界函数：确定目标函数值的估算方法。（关键）
广度优先搜索：根据限界函数，以广度优先方式搜索解空间树，避免无效搜索，从而得到最优解。

2.1 关键问题解决

设计合适的限界函数：
① 估算目标函数值，选取“最有利”的一个子节点作为扩展节点并删除不必要的子节点，简化搜索。要求计算简单、保证最优解在搜索空间中、在搜索早期对不合条件的进行剪枝。
② 方法：具体分析
a.目标函数求最大值：设计估算目标函数上界的限界函数 $ub(s_{i})$ 。通常根节点的ub≥最优解的ub。若 $s_{i}$ 是 $s_{j}$ 的父节点，则 $ub(s_{i})\geqslant ub(s_{j})$ 。
得到一个可行解的 $ub(s_{k})$ 后，将所有小于 $ub(s_{k})$ 的节点剪枝。

b.目标函数求最小值：设计估算目标函数下界的限界函数 $lb(s_{i})$ 。通常根节点的lb≥最优解的lb。若 $s_{i}$ 是 $s_{j}$ 的父节点，则 $lb(s_{i})\leqslant lb(s_{j})$ 。
得到一个可行解的 $lb(s_{k})$ 后，将所有大于 $lb(s_{k})$ 的节点剪枝。
组织活节点表：
用于存放满足限界条件的节点。不同组织方式对应不同搜索方式。
① 队列式：将活节点表组织成队列，按照先进先出原则取下一个扩展节点。
② 优先队列式：将活节点表组织成优先队列，按优先队列排序后的优先级选取下一个扩展节点。可选择小根堆or大根堆。
确定最优解向量：
因为节点处理是跳跃式的，因此搜索到某个叶子节点且对应一个最优解，采用以下两种方式求最优解的各个分量：
① 对每个扩展结点保存从根节点到该节点的路径：比较浪费空间，但实现简单，较常用。
② 在搜索过程中构建搜索经过的树结构：需要给每个节点增加一个指向父节点的指针，当找到最优值时，通过该指针找到对应的最优解向量。

Q：学习过程中的疑惑：为什么广度优先搜索之后的结果就是最优解？

因为广度优先搜索是每搜索到一个节点就扩展它的全部子节点，也就是说，广度优先搜索方法是一层一层依次搜索的。这样的话，只要到达叶子节点，搜索结束，所得到的层数就是最小的，即路径是最短的。

换句话说，如果在搜索过程中已经找到了终点，那么此时的路径一定是从起点开始的最优路径。因为如果路径不是最优路径，那么一定有其他路径更早到达叶子节点，也就比此时已经搜索到的路径更短。

2.2 求目标函数最大值问题的算法描述

3 时空性能分析

3.1 时间性能

最坏情况下，时间复杂度是指数级。
采用限界函数，大范围剪枝，同时根据限界函数不断调整搜索方向，加快了问题的求解速度。

3.2 空间性能

为了得到最优解，每个扩展节点保存该节点到根的路径，或构建搜索树，因此需要额外存储空间。
需要维护待处理节点表HT（通常为优先队列）。
最坏情况下，空间复杂度是指数级。

4 应用

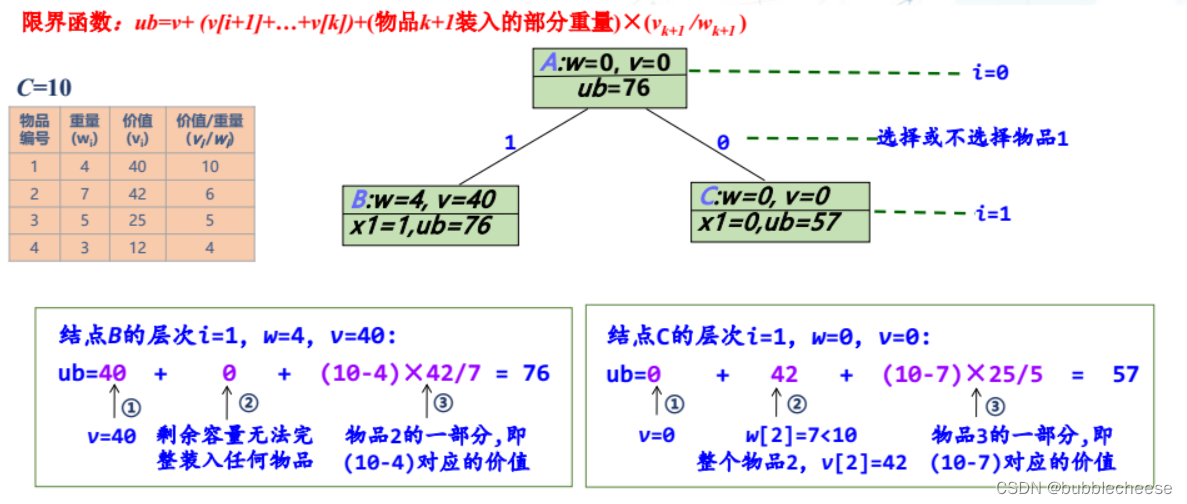
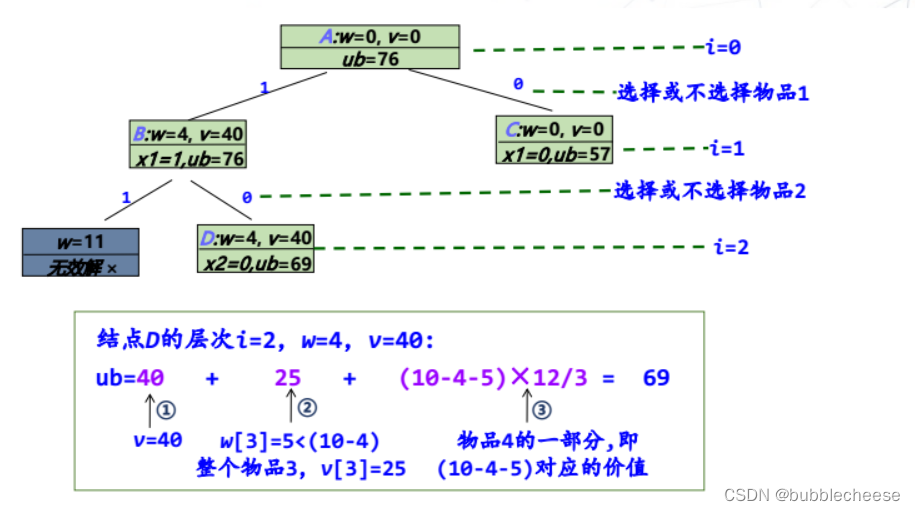
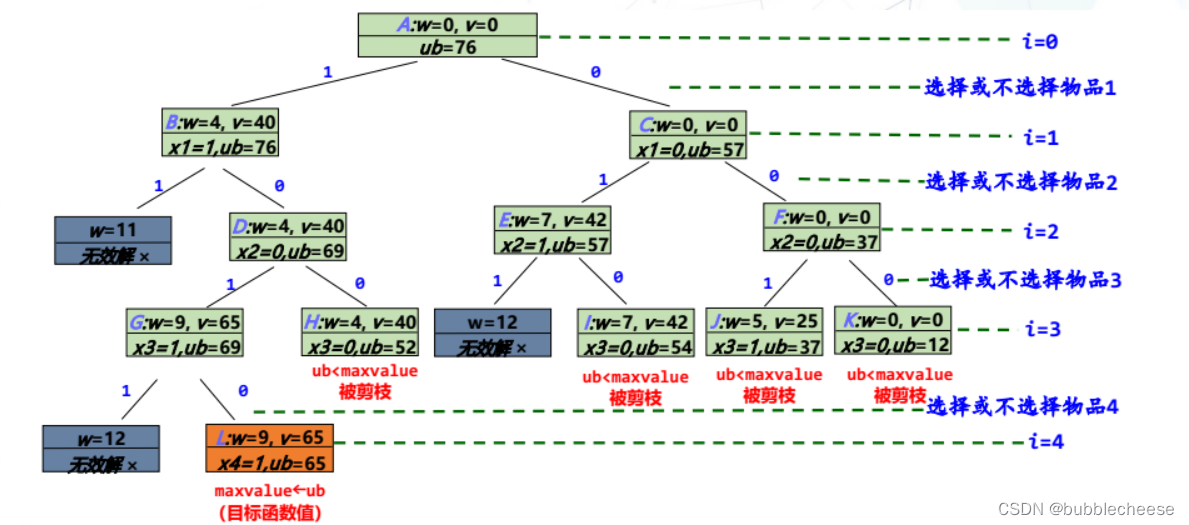
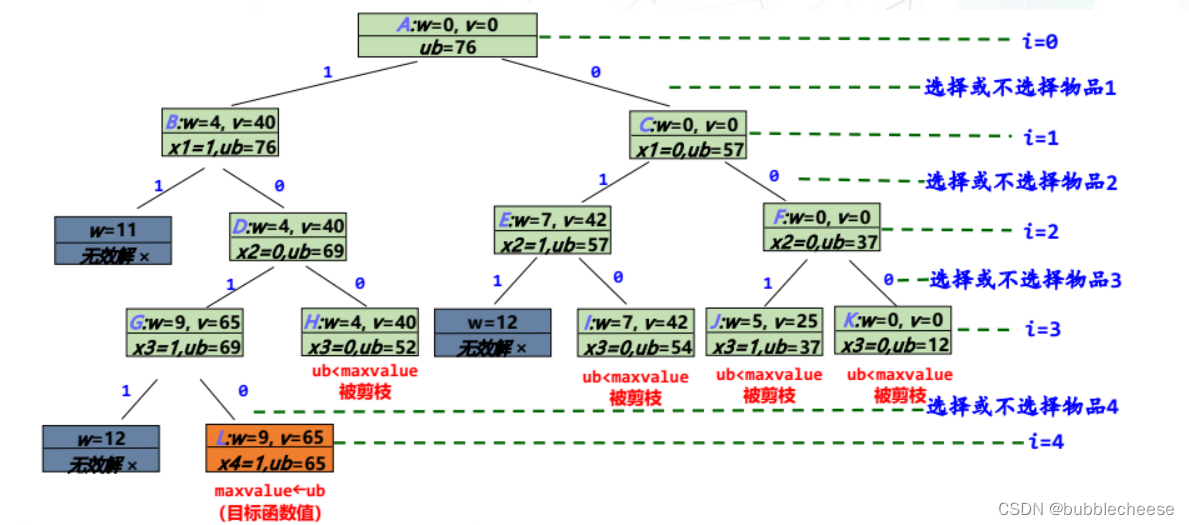
4.1 (0-1)背包问题

（内容来源于课堂课件）

1. 队列式分枝限界法

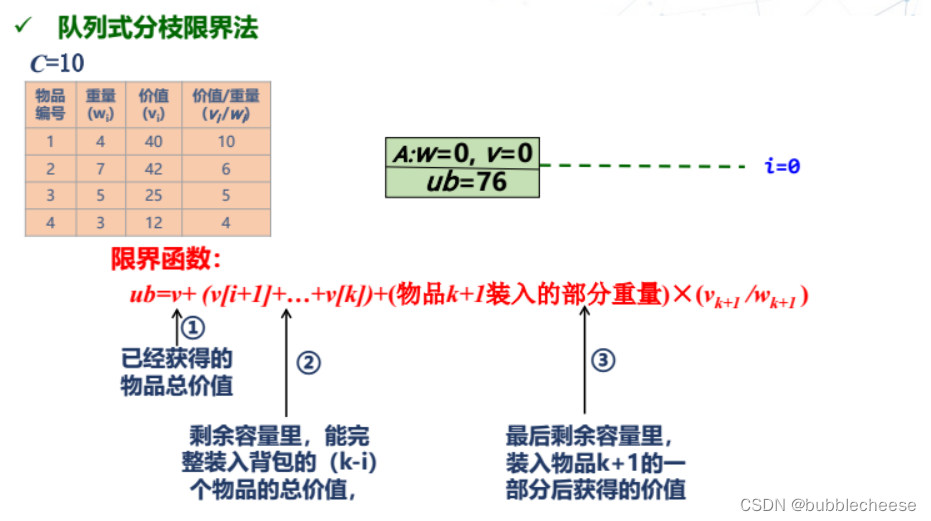
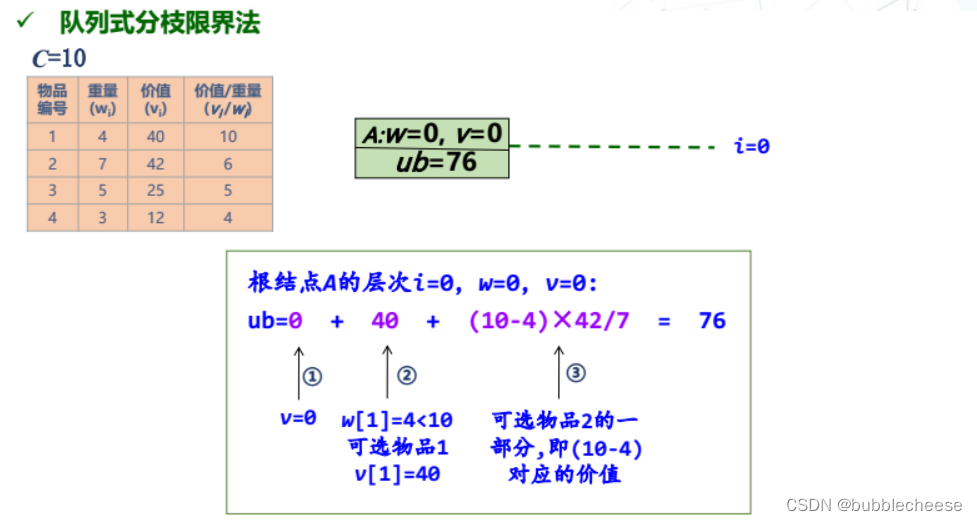
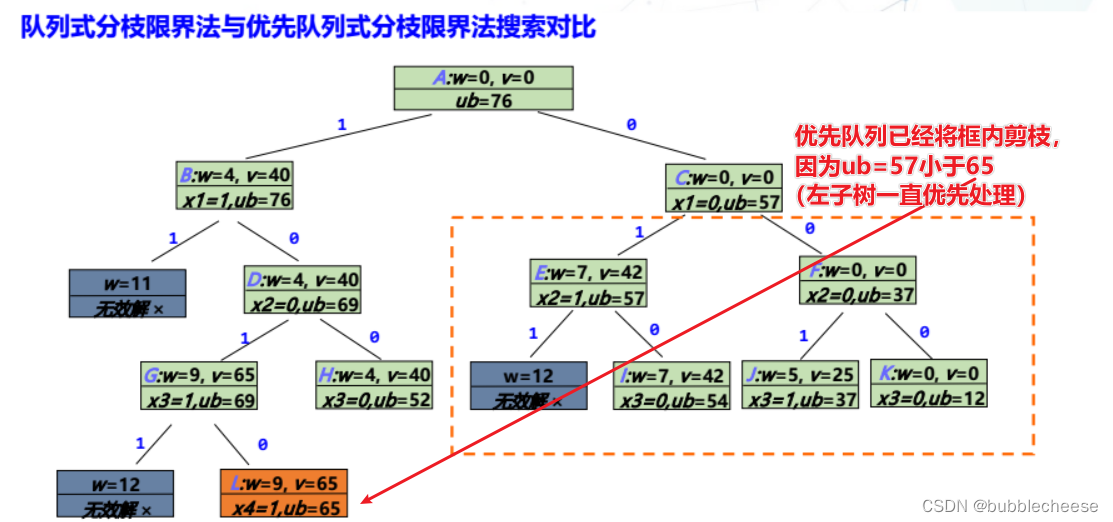
2. 优先队列式分枝限界法

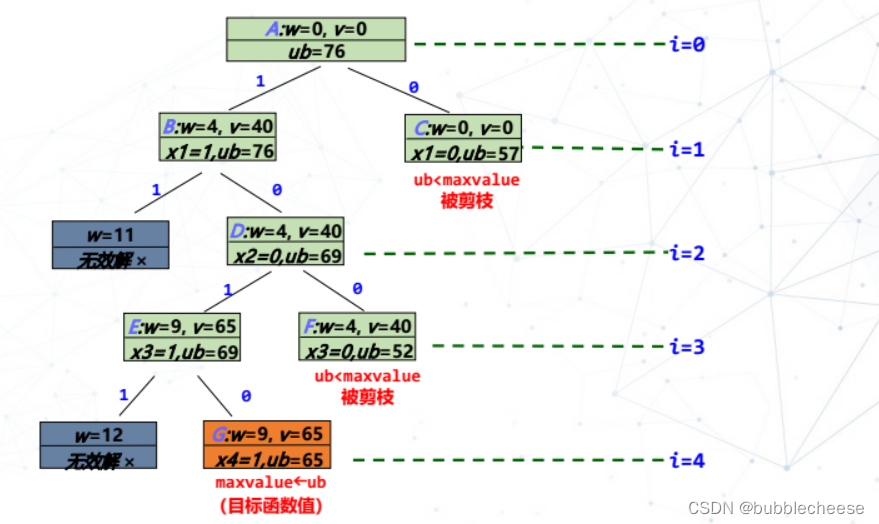
3. 对比

*** 算法伪代码描述及优化 ***

4. 算法分析

4.2 迷宫问题

1.问题描述

定义一个二维数组，例如：
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。

输入格式:
一个5 × 5的二维数组，表示一个迷宫。数据保证有唯一最短路径。

输出格式：
左上角到右下角的最短路径，格式如样例所示。

输入样例：
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

输出样例：
(0,0) (1,0) (2,0) (2,1) (2,2) (2,3) (2,4) (3,4) (4,4)

2.实现步骤：
（1）从入口开始，判断它的上下左右的邻边元素是否满足条件，如果满足条件就引入队列。此处用了一个 R[4][2]的二维数组，用途是可以直接在四次代码循环内，完成用父节点的x,y计算上下左右四个节点的下标，而不用多次写重复的判断代码。用循环代替了分支结构，使代码更加简洁清晰。
（2）取队首元素并将这个元素出队。寻找其相邻且未被访问的元素（用visited数组标记），满足条件的，将其进入队列并标记元素的前驱节点为队首元素。
（3）重复步骤（2），直到队列为空（没有找到可行路径）或者找到了终点。最后从终点开始，根据节点的前驱节点找出一条最短的可行路径。

其中，前驱节点使用类指针标记，最后通过终点的地址一步步往前追溯，得到完整的路径。

参考代码：


using namespace std;
#include <iostream>
#include <queue>
#include <stack>
#define MAX 10
int maze[MAX][MAX];
bool visited[MAX][MAX]; //记录节点是否被访问过
 
 
class Point {
public:
    int x;//行
    int y;//列
    int t; //到这个点所花费的总路程
    Point* before; //指向父状态，用于逆向寻找路径
};
int R[4][2] = {
    -1,0,
    1,0,
    0,-1,
    0,1
};//用于状态扩展(上下左右)
 
Point* BFS() { //返回终点状态
    queue<Point*> q;
    int x = 0, y = 0, t = 0;
    Point* start = new Point(); //函数内部定义的对象，要用new运算符分配空间
    起点初始化
    start->x = 0;
    start->y = 0;
    start->t = 0;
    start->before = NULL;//起点没有父状态
    q.push(start); //起点入队
    while (!q.empty()) {
        Point* tmp = q.front(); //【新建指针指向队头】
        q.pop(); //取出一个节点进行扩展
        for (int i = 0; i < 4; i++) {//遍历四种状态（上下左右）
            x = tmp->x + R[i][0];
            y = tmp->y + R[i][1];
            【skip三连！不满足条件的全部杀杀杀】
            if (x < 0 || x > 4 || y < 0 || y > 4) continue; //数组越界，跳过
            if (visited[x][y]) continue; //访问过，跳过
            if (maze[x][y] == 1) continue; //是墙，跳过
            【可行的，新建节点并入队】
            Point* newtmp = new Point();
            newtmp->x = x;
            newtmp->y = y;
            newtmp->t = tmp->t + 1; //路程为父节点+1
            newtmp->before = tmp; //父节点为tmp
            if (x == 4 && y == 4) return newtmp;//到达终点，则返回终点节点指针
            q.push(newtmp); //新节点入队
            visited[x][y] = true;
        }
        //【结束一轮循环后，一个节点的上下左右都扩展完毕，继续检索子节点】
    }
    return start;
}
int main()
{
    for (int i = 0; i < 5; i++) {
        for (int j = 0; j < 5; j++) {
            cin >> maze[i][j];
            visited[i][j] = false;
        }
    }
    Point* p = BFS();
    stack<Point*> s;
    //将节点从终点开始入栈，然后按出栈顺序输出，则可得到正序的路径
    while (p != NULL) {
        s.push(p);
        p = p->before;
    }
    while (!s.empty()) {
        Point* tmp = s.top();
        s.pop(); //得到节点信息，并出栈
        cout << "(" << tmp->x << "," << tmp->y << ")" << endl;
    }
}

如果看完觉得这篇文章对你有帮助的话，请点个赞支持一下~

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/你好赵伟/article/detail/333097