- 1csdn涨粉技巧篇,都是干货涨粉知识,不花钱的_csdn如何增加阅读量
- 2抖音TikTok快手微信小红书通过intent意图跳转集合详情 URL Scheme 云控auto.js实现intent跳转示例startActivity地址_通过intent的方式抓取scheme地址或者通过小黄鸟抓包抓取
- 3基于 Amazon EKS 搭建开源向量数据库 Milvus_向量数据库部署
- 4DAOS引擎启动流程-源码分析_daos aggregate
- 5JeecgBoot搭建及启动笔记
- 6文档协作编辑 ONLYOFFICE 部署和使用教程_腾讯文档 onlyoffice
- 7ros行为树-概念(基于behaviortree_v3)_行为树 fallback
- 8git :回滚分支_git 分支merge 后回滚
- 9微信小程序 --- 事件处理_微信小程序事件
- 10docker安装Hadoop集群(macOS)_docker上安装hadoop集群 macos
NLP --- 文本分类(基于SVD的隐语意分析(LSA))_nlp语义相关分析
赞
踩
上一节我们详细的讲解了基于VSM的文本分类,这种分类在很早就出现了,虽然是文本分类中有效的分类手段,但是因为建立的向量是很多维的,因此容造成维度灾难,同时VSM的没有能力处理一词多义和一义多词问题,例如同义词也分别被表示成独立的一维,计算向量的余弦相似度时会低估用户期望的相似度;而某个词项有多个词义时,始终对应同一维度,因此计算的结果会高估用户期望的相似度。汉语用户倾向于频繁使用近义词显示“辞藻丰富”“有文化”,不喜重复使用相同词汇。也喜欢使用相关语显示“幽默感”,这是常见语言现象。而VSM无法解决这个样的问题,因此需要提出新的解决方案去解决两个问题:1.维度灾难问题。2.近义词的处理问题。这里解决该问题的思想是来源于矩阵的奇异值分解即SVD算法,通过这个思想提出了LSA算法,因此这里先详细的讲解一下什么是SVD。
SVD算法(Singular Value Decomposition)
这里我是这样安排的,先使用语言进行简单的介绍一下LSA(隐语意模型),因为该模型的思想是基于矩阵的奇异值的分解进行设计的,因此会详细的讲解SVD算法,这里大家需要好好理解SVD这个思想,因为他不仅仅在这里使用,更多的是在推荐系统中使用,因此这里会从推荐系统的一个例子中引入SVD,好,下面开始:
LSA(latent semantic analysis)潜层语义分析,也被称为LSI(latent semantic index),是Scott Deerwester, Susan T. Dumais等人在1990年提出来的一种新的索引和检索算法。该算法和传统向量空间模型(vector space model)一样使用向量来表示词(word)和文档(documents),vsm是通过向量间的关系(如夹角)来判断词及文档间的关系,而不同的 是,LSA将词和文档映射到潜在语义空间,从而去除了原始向量空间中的一些“噪音”,提高了信息检索的精确度。我们下面就先从推荐系统的角度简单的解释一下,什么是浅语意空间。
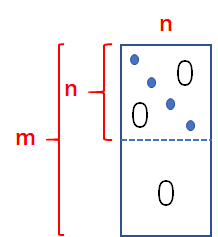
这里简单的根据推荐系统来说,这里使用给用户推荐电影的例子来解释,首先我们会得到一个评分矩阵,这个矩阵呢它的行是item(主题),如果推荐的是电影的话,那么item就是电影名了,而列就是用户了即user,我们从不同的用户中就可以得到这样的评分矩阵,如下所示:

现在的问题是,1、这个评分矩阵很大。2、这个矩阵是稀疏,什么意思呢?假如这个矩阵是给电影评分的,那么我们不能得到所有用户给所有的电影评分,因此这个矩阵中会有很多的空缺值。因此推荐系统中会有这两个问题的存在,如何解决呢?这里使用的是SVD 进行解决,我们看看他是如何解决推荐系统的两个问题的,其实很简单,如下图所示:
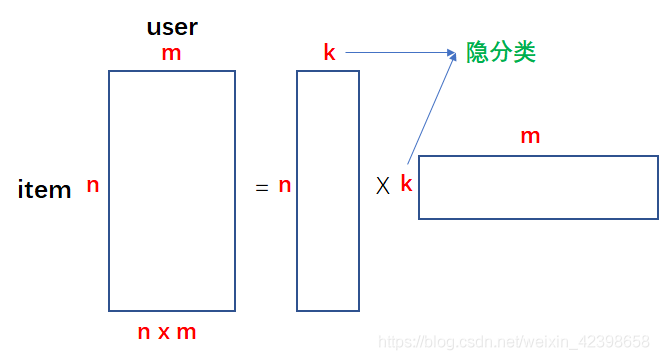
假如我们的评分矩阵是nxm的矩阵,其中m代表user,n代表item,我们可以通过两个矩阵的相乘的形式得到评分矩阵,写成上图等号右边的形式,上图我们可看到评分矩阵可以通过nxk的矩阵和kxm的矩阵相乘得到,这里的k是隐分类的意思,这里的隐分类不是我们人为划分的,一般都是我们通过矩阵分解以后得到这个k,然后通过两个矩阵的内容进行判断,隐分类的含义,这里以电影评分矩阵进行比喻,一旦通过矩阵分解成上面的形式,我就可以得到电影评分的矩阵分解了,就会得到隐分类了,此时我们观察分解后的矩阵就会发现,隐分类代表的是某一类型电影,如上图等号右边的第一个矩阵即nxk矩阵,就是说对这n个电影给出概率或者打分来说明他是属于电影的哪一类如科幻、爱情、恐怖等等,此时的k就是代表电影的类型了也就是隐分类了,根据每部电影的行中不同的值来判断它属于那个电影类型的概率,这就是上图等号右边第一个矩阵的含义,那么等号右边的后面的那个矩阵代表什么呢?其实很类似的分析,每个用户代表着一列,那么每行代表在不同类型的电影,我们通过分析用户观看哪种类型的电影概率或者评分最高,以此来给用户推荐他喜欢的类型电影,由此我们可以发现在电影的评分中隐分类就代表着电影的类型,而分解后的两个矩阵对我们都很有用,这就是我们k的物理意义和分解后矩阵代表的含义,但是我们还没解释他是如何解决推荐系统的两个问题的,下面我们就来解释一下:假如我们分解后的矩阵的k值通常要比n和m小的多数值,如n=100万部电影,k=100种类型,m=100万人,我们来计算一下分解后的数据有多少个:nxk+kxm = 100万x100 + 100x100万 = 2亿个数据,需要2亿个存储单元,我们看看原始评分矩阵的大小:nxm= 100万x100万=10000亿,可想而知,存储量很大,因此矩阵分解可以起到降维、压缩数据的作用。因为数据压缩了其实就解决了稀疏性的问题,稍后大家会看到如何解决的,上面就是推荐系统的应用,那么在文本分类是如何使用的呢?
LSA(latent semantic analysis)潜在语义分析
在文本的分类中和在推荐系统中的应用很类似,这里简单的讲解一下:
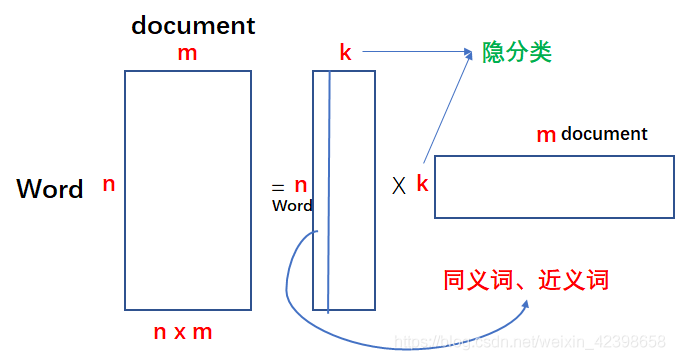
在VSM中我们知道,每篇文章我们都可以构造一个词向量,这样由多篇文章就可以构成一个矩阵,如上图的等号左边的图,这里的m就是文章数了,n就是每个词袋的元素数了,通过矩阵分解后就会得到像上图等号右边的第一个矩阵形式,和推荐系统类似,这里的k代表的就是隐分类,他的物理意义就是说在每个词向量(文本)的元素中概率或者评分相近的词,就是同义词和近义词了,那么第二个矩阵就相当于降维了,即我们关键的信息留下来,同义词和近义词我们按照左边的分解取一个概率最大的表示,如我们讨论两个文本是否相似时,我们知道评分矩阵的维度是很大,而且还是稀疏的,但是我们通过矩阵分解以后就会得到隐特征,即主要的信息都保存下来了,此时我们的矩阵就不在是稀缺了,这也就解释了为什么起到降维和解决稀疏矩阵的原理了,这里大家不应太纠结隐分类到底代表什么,我们不需要知道,只需要判断即可,这就是SVD用在文本分类中的原理,因为文本分类是最早使用SVD的,因此,推荐系统是借鉴了文本分类的应用才研究出推荐系统的,这里就不在过多讨论了,大家肯定想知道,这个矩阵分解到底是如何做呢?怎么得到这个k的值呢?如何确定呢?是人为确定还是自动生成呢?我们我们的主要精力就来看看SVD到底是如何分解的。下面的内容需要大家有一定的矩阵方面的知识,如果有看不懂的建议看看矩阵论相关的书籍进行补充一下基础知识,建议看张贤达的《矩阵分析与应用》第六章365页的内容,那里有详细的定义,这里我会很直观的进行讲解,数学方面的推倒大家可以参考这本书。
SVD分解过程推倒
在矩阵里有这样一个定理或者性质即:
定理:令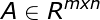
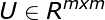
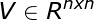
![]()
式子中:
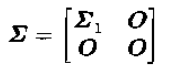
且:
![]()
其中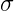
![]()
上面就是奇异值分解的定义了,下面就给大家形式的讲解一下是怎么推倒的,大家看完以后最好看看张贤达书中的数学推倒,这样更好 。下面我们开始:
其中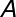
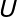

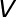

如上图
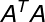

我们知道方阵一定是半正定的,即一定存在逆矩阵的,一定存在特征值和特征向量的。我们的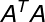

如果有矩阵知识的同学应该能看到其实 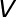
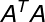
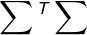

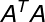
上面我们就是SVD的分解了,但是我们需要的形式应该是下面的样式呀:

我们就根据上面的式子继续推倒,慢慢到我们上面的形式,下面继续:
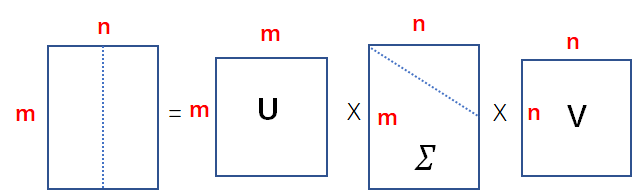
这里我们按照SVD的形式把mxn的矩阵给分解了,如上图形式,其中 

如上图我们只取前k个特征值,同时把

此时我们按照块进行矩阵运算得到下面的式子:

从上图的计算可知,最后的矩阵可以写成①x③x⑦的形式,我们在再分别看看这三个矩阵的形式:
①矩阵的维度是mxk的
③矩阵的维度是kxk的
⑦矩阵的维度是kxn的
此时我们把③的矩阵写两个矩阵相乘的形式如下:

所以最终A的矩阵可以写成如下形式:

这样我们等号右边的第一个矩阵和第二个矩阵分别把两个kxk矩阵吸收了,最后就形成了我们刚开始要求的矩阵了即:
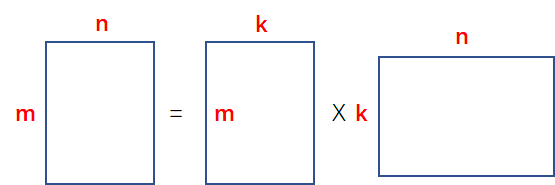
这既是推倒,具体的数学推倒建议看看张贤达的书,那里有更详细的推倒和更全面的讲解,这里只是让大家更容易理解而已,
好了,本节到此结束下一节我们看看改进的LSA(latent semantic analysis)潜在语义分析的算法即PLSA算法。