- 1彻底讲透:高并发场景下,MySQL处理并发修改同一行数据的安全方法_多个用户修改同一个mysql数据,mysql悲观锁
- 2对象存储服务MinIO_minio服务
- 3winscp通过跳板机访问远程服务器(使用秘钥的方式传输文件)_winscp 隧道 跳板机上的密码
- 4Flink项目(看了就会)_flink 项目
- 5AI动画制作:从手绘到智能创作_ai在动画设计的发展
- 6用docker-compose 搭建 rabbitmq集群_docker compose rabbitmq
- 7AI Challenger 植物病害识别项目:利用深度学习守护绿色世界
- 8年入100万的程序员说,看完这些书至少涨薪10万_java程序猿如何年入百万
- 9Unity 3D之UI设置父子关系Instantiate 和 setParent坑_unity instantiate ui
- 10package info not found issue_pms的getpackageinfo找不到对应的包
[⑤5G NR]: 5G Polar编码算法_5g polar码编码标准
赞
踩
前言
博主在[①5G NR]: 3GPP协议中Polar编码流程解读中介绍了5G中Polar码编码的相关流程,在这篇博客中就介绍下在5G中Polar码基础编码的算法,Polar码(极化码)的发明者是Erdal Arikan教授。
Arikan kernel
首先来介绍下什么是Arikan kernel。Arikan kernel或者Arikan matrix是个 2 ∗ 2 2*2 2∗2的矩阵:
G
2
=
[
1
0
1
1
]
G_2=
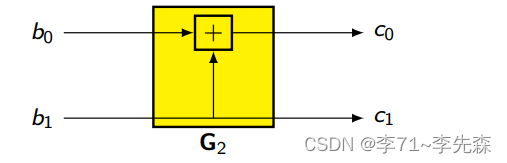
对于最基础情形, b ‾ = [ b 0 , b 1 ] \underline{b}=[b_0, b_1] b=[b0,b1]为信息比特序列, c ‾ = [ c 0 , c 1 ] \underline{c}=[c_0, c_1] c=[c0,c1]为码字比特序列,那么就满足:
c ‾ = b ‾ ⋅ G 2 \underline{c}=\underline{b}\cdot G_2 c=b⋅G2
结果可以由下图来描述:
生成矩阵 G N G_N GN
Polar码的长度为 N = 2 n N=2^n N=2n,根据协议章节5.3.1.2,Polar码的生成矩阵 G N G_N GN由 G 2 G_2 G2通过Kronecker prodcut(克罗内克内积)计算得到:
G
N
=
G
2
n
=
G
2
⊗
G
2
n
−
1
=
[
G
2
n
−
1
0
G
2
n
−
1
G
2
n
−
1
]
=
(
G
2
)
⊗
n
G_N=G_{2^n}=G_2\otimes G_{2^{n-1}}=
如果 u ‾ = [ u 0 , u 1 , . . . , u N − 1 ] \underline{u}=[u_0,u_1,... ,u_{N-1}] u=[u0,u1,...,uN−1]为编码前的输入的信息比特序列, d ‾ = [ d 0 , d 1 , . . . , d N − 1 ] \underline{d}=[d_0,d_1,... ,d_{N-1}] d=[d0,d1,...,dN−1]为编码后的输出的码字比特序列,那么就满足:
d ‾ = u ‾ ⋅ G N \underline{d}=\underline{u}\cdot G_N d=u⋅GN
样例 N = 8 N=8 N=8
Polar码码字的结果可以通过(recursive encoding)迭代的方式计算得出,以 N = 2 3 = 8 N=2^3=8 N=23=8为例,可以通过迭代3次计算得出,首先生成矩阵 G 8 G_8 G8为:
G
8
=
G
2
⊗
G
2
⊗
G
2
=
[
1
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
1
0
1
0
0
0
0
0
1
1
1
1
0
0
0
0
1
0
0
0
1
0
0
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
0
1
1
1
1
1
1
1
1
]
G_8=G_2\otimes G_2 \otimes G_2=
记 u ‾ ( n ) \underline{u}^{(n)} u(n) 为第n次迭代,那么3次迭代的过程见下图:
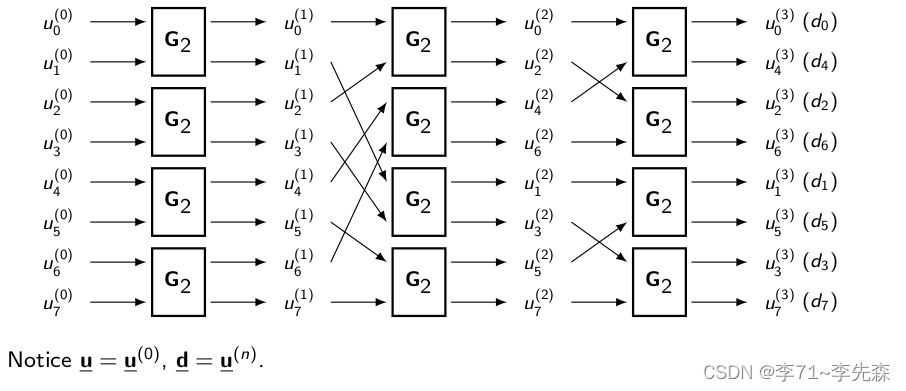
如果 u ‾ = [ 0 , 0 , 0 , 1 , 0 , 1 , 1 , 1 ] \underline{u}=[0,0,0,1,0,1,1,1] u=[0,0,0,1,0,1,1,1],那么
u
‾
(
1
)
=
[
0
,
0
,
1
,
1
,
1
,
1
,
0
,
1
]
\underline{u}^{(1)}=[0,0,1,1,1,1,0,1]
u(1)=[0,0,1,1,1,1,0,1]
u
‾
(
2
)
=
[
1
,
1
,
1
,
1
,
1
,
0
,
0
,
1
]
\underline{u}^{(2)}=[1,1,1,1,1,0,0,1]
u(2)=[1,1,1,1,1,0,0,1]
u
‾
(
3
)
=
[
0
,
1
,
1
,
0
,
1
,
0
,
0
,
1
]
\underline{u}^{(3)}=[0,1,1,0,1,0,0,1]
u(3)=[0,1,1,0,1,0,0,1]
d
‾
=
u
‾
⋅
G
8
=
[
0
,
1
,
1
,
0
,
1
,
0
,
0
,
1
]
\underline{d}=\underline{u}\cdot G_8=[0,1,1,0,1,0,0,1]
d=u⋅G8=[0,1,1,0,1,0,0,1]


