二叉堆/堆排序概念理解以及Java语言实现（学习笔记）_画出第一趟排序后新堆对应的完全二叉树

二叉堆/堆排序概念理解以及Java语言实现（学习笔记）

1.基础概念介绍

（1）满二叉树：每一层都达到了最大节点数，高度为h的满二叉树节点数为pow(2,h)-1 ( pow(x,y)代表x^y )

如图所示：

（2）完全二叉树：高度为h的二叉树每一个节点都和高度为h的满二叉树节点编号一一对应，那么它就是满二叉树。

如图所示：

	[1] 高度为h的完全二叉树节点数取值范围[pow(2,h-1),pow(2,h)-1],可见完全二叉树的高度是O( log(n) )
	
	[2] 满二叉树是特殊的完全二叉树

	[3]根节点编号记为1，对于节点i，它的左孩子编号为2i，右孩子编号为2i+1,对于节点i，它的父节点为floor(i/2) (floor表示向下取整)。完全二叉树适合用顺序存储结构来表示
1
2
3
4
5

（4）二叉堆概念：

[1] 首先是一颗完全二叉树

[2] 小根堆：任何一个节点小于等于它的左孩子且小于等于他的右孩子

[3] 大根堆：任何一个节点大于等于它的左孩子且大于等于他的右孩子
1
2
3
4
5

举个例子（大根堆）：

2.堆排序

[1] 堆排序属于选择排序，第i趟在n-i+1个元素中选择最大（值），作为子序列的第i个元素。

[2]和AVL树、红黑树、B树和B+树不同，他们是用于查找的，但堆是用于排序的。

2.1 建立大根堆（在已有序列基础上建立）

设序列长度为n，则最后一个父节点编号为floor(n/2) （floor表示向下取整）

	[1]  i=floor(n/2),查看节点i和它的孩子，如果节点i小于两个（也可能是一个）孩子的最大值，则把节点i和最大孩子交换
	
	[2] 令i减少1，查看节点i和它的孩子，如果节点i小于两个（也可能是一个）孩子的最大值，则把节点i和最大孩子交换，以交换后的孩子为根节点的树可能不再满足堆的定义，如果不满足需要对它进行调整（下调）（多级的调整）
	
	[3] 重复[2]，直到i=1
1
2
3
4
5

如图：

空间复杂度：O(1)

时间复杂度：O(n)

Java实现：

实际上Java可以比较任何对象的大小，我的上篇博客有讲到（https://blog.csdn.net/weixin_42111859/article/details/104132520），这里用int数组（ArrayList更合适，可以动态添加删除，更加灵活）举个例子：

    // 从0编号，i左孩子为2i+1，右孩子为2i+2，父节点为(i+1)/2-1
    private static void buildMaxHeap(int[] array) {
        for (int i = array.length / 2 - 1; i >= 0; i--) {
            adjustDown(i, array);
        }
    }

    // 使得i为顶点的子树成为堆
    private static void adjustDown(int i, int[] array) {
        for (int j = i; j < array.length; ) {
            // k为较大的孩子
            int k;
            // 有两个孩子
            if (array.length >= 2 * j + 3) {
                k = array[2 * j + 1] > array[2 * j + 2] ? 2 * j + 1 : 2 * j + 2;
            }
            // 只有左孩子
            else if (array.length >= 2 * j + 2) {
                k = 2 * j + 1;

            }
            // 没有孩子
            else {
                break;
            }
            // 父节点更大，不必交换
            if (array[j] >= array[k]) {
                break;
            }
            // 交换
            int temp = array[j];
            array[j] = array[k];
            array[k] = temp;
            j = k;
        }
    }

    @Test
    public void testBuildMaxHeap() {
        int[] a = {1, 2, 3, 4, 5, 6, 7, 8, 9};
        System.out.println(Arrays.toString(a));
        buildMaxHeap(a);
        System.out.println(Arrays.toString(a));
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

控制台输出结果：

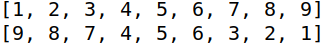
代码和上面的例子是对应的

2.2 堆排序

第i趟，先取堆顶元素（堆顶一定是最大值），然后把堆底赋给堆顶，对n-i个元素下调（建立大根堆）

这也是不断删除最大元素的过程

时间复杂度：O( n*log(n) )

空间复杂度：O(1) 下面代码中用一个数组存储结果了，实际上可以输出或者用迭代器返回结果，只需要常数个辅助单元

如果只求前m大的值，时间复杂度为 O( m*log(n) )

java代码：

public static int[] heapSort(int[] array) {
        buildMaxHeap(array);
        int[] rlt = new int[array.length];
        int index = 0;
        for (int i = array.length - 1; i >= 0; i--) {
            // 保存堆顶元素
            rlt[index++] = array[0];
            // 堆底给堆顶
            array[0] = array[i];
            // 构建大根堆
            adjustDown(0, array, i);
        }
        return rlt;

    }

    @Test
    public void testHeapSort() {
        int[] a = {1, 2, 3, 4, 5, 6, 7, 8, 9};
        System.out.println(Arrays.toString(a));
        System.out.println(Arrays.toString(heapSort(a)));
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

运行结果为：

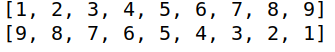
2.3 堆的插入
堆是可以插入元素的，尾接新元素，如果比父元素更大就交换，然后重复这个步骤（上调）

举一个例子（不写代码了）：

转载请注明出处，谢谢合作