热门标签
热门文章
- 1Python实现http接口自动化测试的示例代码_python http接口测试工具 文档生成
- 2Vue响应式原理以及实现_vant vue响应式编程
- 3智能降重论文 神码ai
- 4python照片处理生成3d模型_【神器】摄影实时建模,用照片生成3D模型
- 5QLExpress计算等本等息、等额本息、等额本金_addfunctionofclassmethod
- 6改进YOLOv8 | 特征融合优化 | YOLOv8引入BiFPN结构 | EfficientDet:高效可扩展目标检测
- 7YOLOv7保姆级教程!(个人踩坑无数)----环境配置_yolov7环境搭建
- 8AIGC实战——GPT(Generative Pre-trained Transformer)
- 9OWASP Mantra渗透测试框架安装及使用
- 10Ubuntu下安装配置Android SDK_ubuntu android sdk linux
当前位置: article > 正文
opencv 曲线拟合_opencv拟合曲线
作者:2023面试高手 | 2024-03-18 15:29:51
赞
踩
opencv拟合曲线
最小二乘法多项式曲线拟合原理与实现 最小二乘法多项式曲线拟合原理与实现_JairusChan的技术博客-CSDN博客_曲线拟合的最小二乘法
算法+OpenCV】基于opencv的直线和曲线拟合与绘制(最小二乘法) 算法+OpenCV】基于opencv的直线和曲线拟合与绘制(最小二乘法) - feng..liu - 博客园



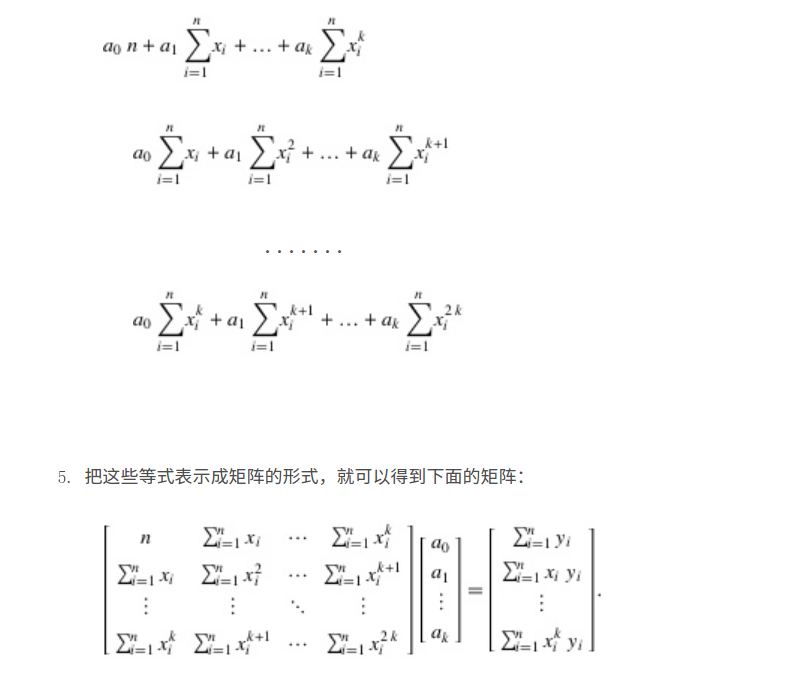

基于opencv c++代码如下:
- #include <iostream>
- #include <opencv.hpp>
- #include<opencv2/opencv.hpp>
-
- using namespace std;
- using namespace cv;
-
- void FitPolynomialCurve(const std::vector<cv::Point>& points, int n, cv::Mat& A){
- //最小二乘法多项式曲线拟合原理与实现 https://blog.csdn.net/jairuschan/article/details/7517773/
- //https://www.cnblogs.com/fengliu-/p/8031406.html
- int N = points.size();
- cv::Mat X = cv::Mat::zeros(n + 1, n + 1, CV_64FC1);
- for (int i = 0; i < n + 1; i++){
- for (int j = 0; j < n + 1; j++){
- for (int k = 0; k < N; k++){
- X.at<double>(i, j) = X.at<double>(i, j) +
- std::pow(points[k].x, i + j);
- }
- }
- }
- cv::Mat Y = cv::Mat::zeros(n + 1, 1, CV_64FC1);
- for (int i = 0; i < n + 1; i++){
- for (int k = 0; k < N; k++){
- Y.at<double>(i, 0) = Y.at<double>(i, 0) +
- std::pow(points[k].x, i) * points[k].y;
- }
- }
- A = cv::Mat::zeros(n + 1, 1, CV_64FC1);
- cv::solve(X, Y, A, cv::DECOMP_LU);
- }
-
-
- int main(int argc, char **argv)
- {
- string path = "/data_1/everyday/1224/2.jpeg";
- Mat img = imread(path);
- Mat img_gray,img_bi;
- cvtColor(img,img_gray,CV_BGR2GRAY);
- threshold(img_gray,img_bi,80,255,THRESH_BINARY_INV);
-
- vector<vector<Point> > contours;
- vector<Vec4i> hierarchy;
- findContours( img_bi, contours, hierarchy, CV_RETR_EXTERNAL, CV_CHAIN_APPROX_SIMPLE , Point(0, 0) );
- std::cout<<contours[0].size()<<std::endl;
-
- cv::Mat img_draw = cv::Mat(img.rows,img.cols,CV_8UC3,Scalar(0,0,255));
- drawContours(img_draw,contours,-1,Scalar(255,255,255));
-
-
- int n = 3;
- cv::Mat A;
- FitPolynomialCurve(contours[0], n, A);
- std::vector<cv::Point> points_fitted;
- for (int x = 0; x < 800; x++)
- {
- double y = A.at<double>(0, 0) + A.at<double>(1, 0) * x +
- A.at<double>(2, 0)*std::pow(x, 2) + A.at<double>(3, 0)*std::pow(x, 3);
- points_fitted.push_back(cv::Point(x, y));
- }
-
- cv::polylines(img_draw, points_fitted, false, cv::Scalar(0, 0, 0), 1, 8, 0);
-
- imshow("img_src",img);
- imshow("img_draw",img_draw);
- imshow("img_bi",img_bi);
- waitKey(0);
-
-
- return 0;
- }

效果图如下:
但是我后面又整了个S形状的图像,找不到能够很好拟合的函数阶数。
- #include <iostream>
- #include <opencv.hpp>
- #include<opencv2/opencv.hpp>
-
- using namespace std;
- using namespace cv;
-
- void FitPolynomialCurve(const std::vector<cv::Point>& points, int n, cv::Mat& A){
- //最小二乘法多项式曲线拟合原理与实现 https://blog.csdn.net/jairuschan/article/details/7517773/
- //https://www.cnblogs.com/fengliu-/p/8031406.html
- int N = points.size();
- cv::Mat X = cv::Mat::zeros(n + 1, n + 1, CV_64FC1);
- for (int i = 0; i < n + 1; i++){
- for (int j = 0; j < n + 1; j++){
- for (int k = 0; k < N; k++){
- X.at<double>(i, j) = X.at<double>(i, j) +
- std::pow(points[k].x, i + j);
- }
- }
- }
- cv::Mat Y = cv::Mat::zeros(n + 1, 1, CV_64FC1);
- for (int i = 0; i < n + 1; i++){
- for (int k = 0; k < N; k++){
- Y.at<double>(i, 0) = Y.at<double>(i, 0) +
- std::pow(points[k].x, i) * points[k].y;
- }
- }
- A = cv::Mat::zeros(n + 1, 1, CV_64FC1);
- cv::solve(X, Y, A, cv::DECOMP_LU);
- }
-
- int main(int argc, char **argv)
- {
- string path = "/data_1/everyday/1224/3.jpeg";
- Mat img = imread(path);
- Mat img_gray,img_bi;
- cvtColor(img,img_gray,CV_BGR2GRAY);
- threshold(img_gray,img_bi,80,255,THRESH_BINARY_INV);
-
- vector<vector<Point> > contours;
- vector<Vec4i> hierarchy;
- findContours( img_bi, contours, hierarchy, CV_RETR_EXTERNAL, CV_CHAIN_APPROX_SIMPLE , Point(0, 0) );
- std::cout<<contours[0].size()<<std::endl;
-
- cv::Mat img_draw = cv::Mat(img.rows,img.cols,CV_8UC3,Scalar(0,0,255));
- drawContours(img_draw,contours,-1,Scalar(255,255,255));
-
-
- int n = 9;
- cv::Mat A;
- FitPolynomialCurve(contours[0], n, A);
- std::vector<cv::Point> points_fitted;
- for (int x = 0; x < 800; x++)
- {
- double y = A.at<double>(0, 0) + A.at<double>(1, 0) * x +
- A.at<double>(2, 0)*std::pow(x, 2) + A.at<double>(3, 0)*std::pow(x, 3) + A.at<double>(4, 0)*std::pow(x, 4) + A.at<double>(5, 0)*std::pow(x, 5)
- + A.at<double>(6, 0)*std::pow(x, 6) + A.at<double>(7, 0)*std::pow(x, 7) + A.at<double>(8, 0)*std::pow(x, 8) + A.at<double>(9, 0)*std::pow(x, 9);
- //+ A.at<double>(10, 0)*std::pow(x, 10) + A.at<double>(11, 0)*std::pow(x, 11) + A.at<double>(12, 0)*std::pow(x, 12);
- points_fitted.push_back(cv::Point(x, y));
- }
-
- cv::polylines(img_draw, points_fitted, false, cv::Scalar(0, 0, 0), 1, 8, 0);
-
-
- imshow("img_src",img);
- imshow("img_draw",img_draw);
- imshow("img_bi",img_bi);
- waitKey(0);
-
-
- return 0;
- }

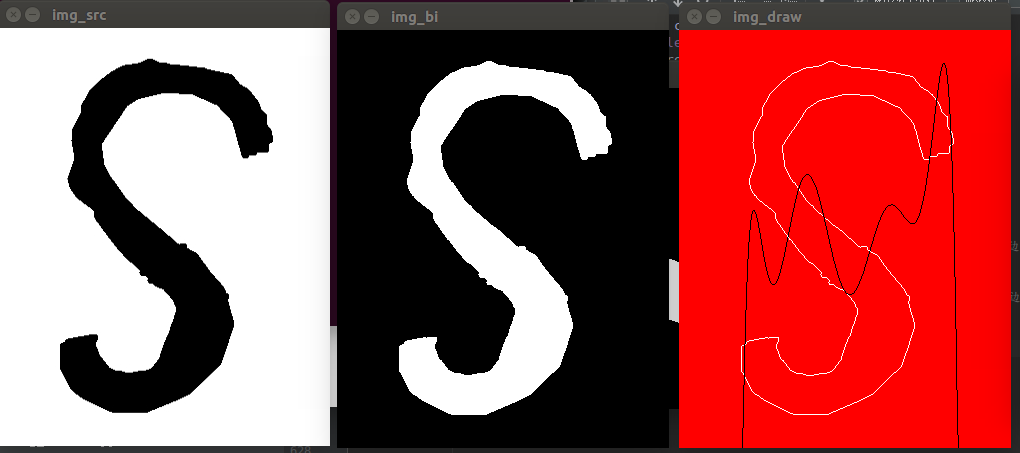
突然想明白,这个S形状曲线一个x对应好几个y,不行。需要一个x唯一对应一个y的曲线才能拟合。然后又顺手画了一个,果真可以拟合。

当然代码每次根据不同的阶数写好多A.at(6, 0)*std::pow(x, 6),可以用如下函数自动根据x得到y:
- double CurveY(double x, cv::Mat& A){
- double y = 0.0;
- double *a = A.ptr<double>();
- for (int i = 0; i < A.rows; i++){
- y += a[i] * pow(x, i);
- }
- return y;
- }
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/2023面试高手/article/detail/264023
推荐阅读
相关标签


