假设检验，显著性，置信水平，p值，点估计_置信水平 p值

​

1、为什么需要假设检验？

以下图激光器项目为例子，抽样30个，改善前720mw，改善后723mw，有一点提升，提升小，可能是正常的波动，所以不一定真的提升了。所以到底是正常波动还是真的改善了？需要结合功率标准差进行分析。

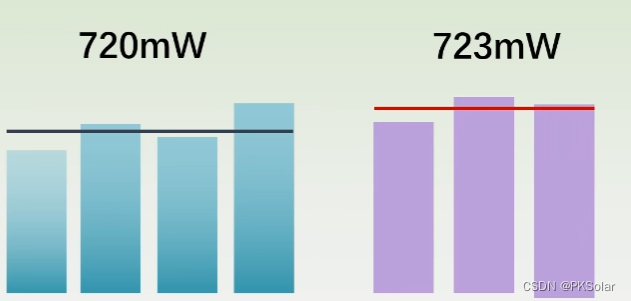
​​标准差决定了波动的情况。如果激光功率标准差极小，几乎不可能波动到723mw，如下图，波动到723mW已经十分罕见。则其实可以看出，改善后激光功率是有提高的。

​​
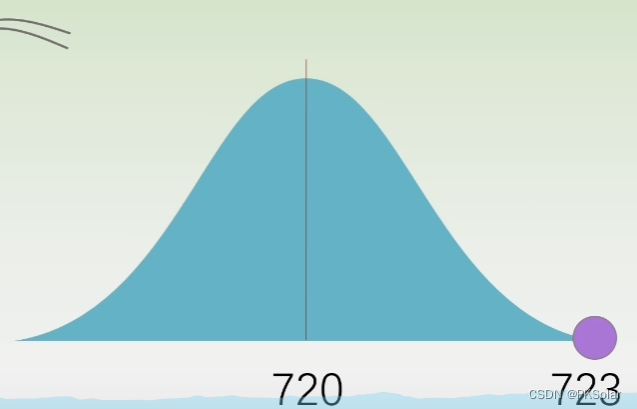
再比如灯泡的良品率，改善后提升了7%,但是有可能原本灯泡良品率的波动很大，因此也不能说真的有改善。

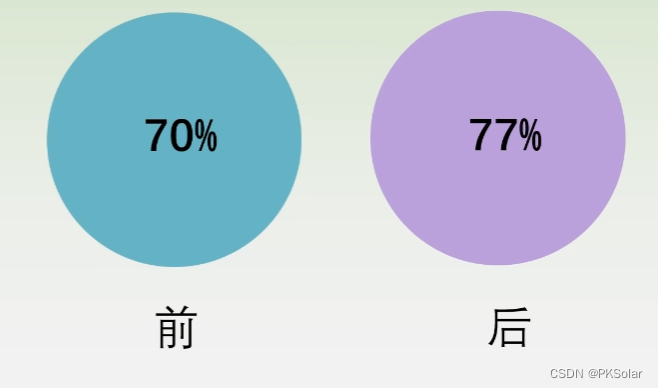
如下图，7%的波动很正常。所以不能说真有提升。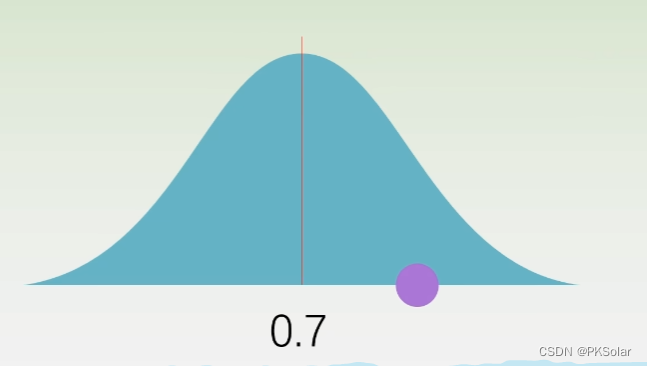

2、显著性水平与置信水平

那么怎么判断是否真的有提升？Fisher提出5%的显著水平
如下改善前激光器的功率概率分布图，整个区域的累计概率是1,。红色区域是0.05的累计概率
如果改善后抽样的样本均值落在这个红色区域，那可以说，这批改善后的样本和改善前的样本显著不一样。

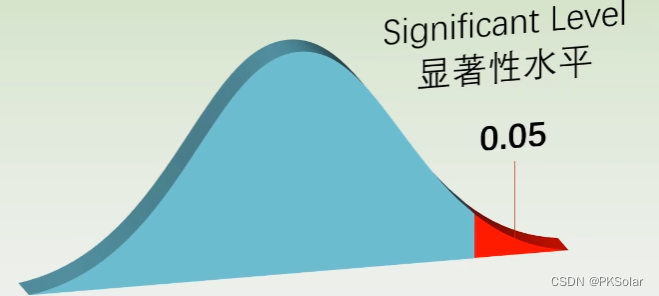
剩下的累积概率，0.95就是置信水平。如果得到的数据在0.05内，说明是同一批样品，没有差别。

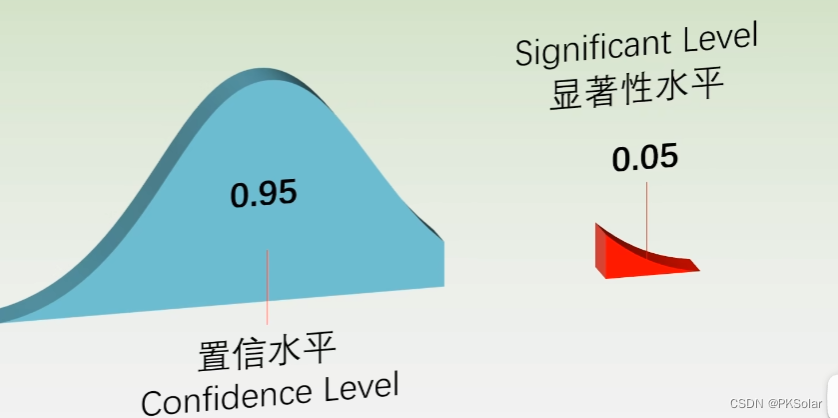
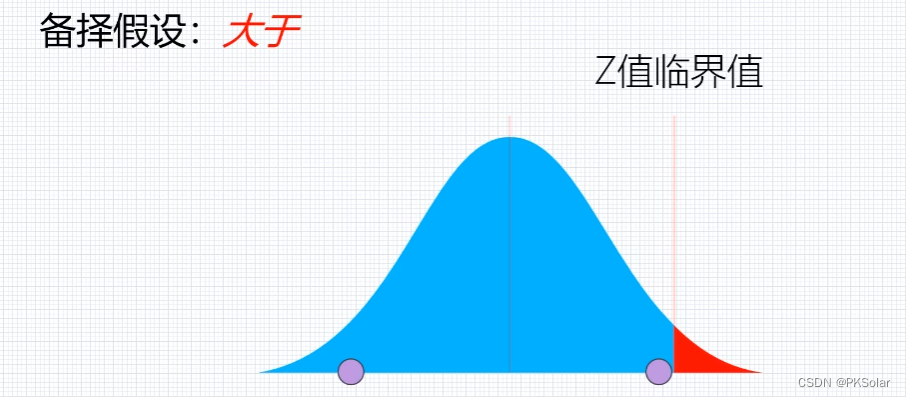
这里只值提到单侧，是否大于的情况。
还可以检测是否小于（左侧），还是否等于（双侧。）
如下图，检测墨西哥的收入是否等于中国，如果抽样的均值落在左边或者右边，都意味着不等于。

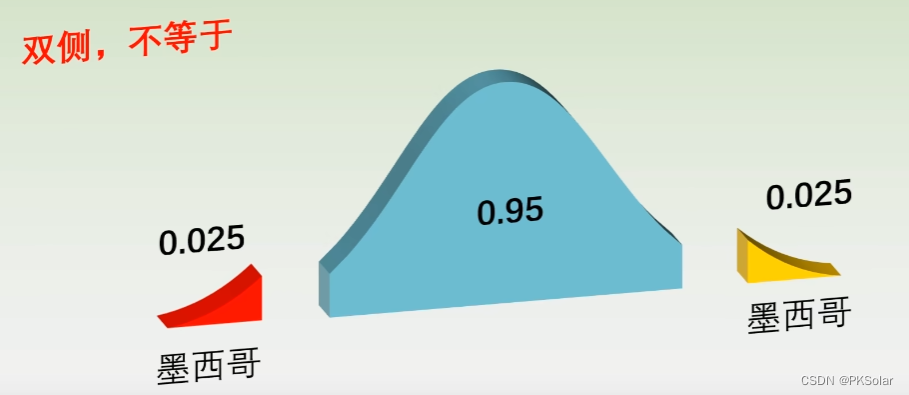
3、假设检验思想

原假设，比如激光器改善前后没多大区别，是一个正态分布。（通常会被打破）
备择假设，要和实验目的相同，比如激光器改善后提升了。有了显著提升

如下图，绿色为改善前，黄色为改善后的假设，是和绿色相同，蓝色是实际抽取30个的分布，根据中心极限定理和之前的假设，会服从正态分布，并且其标准偏差公式如下：

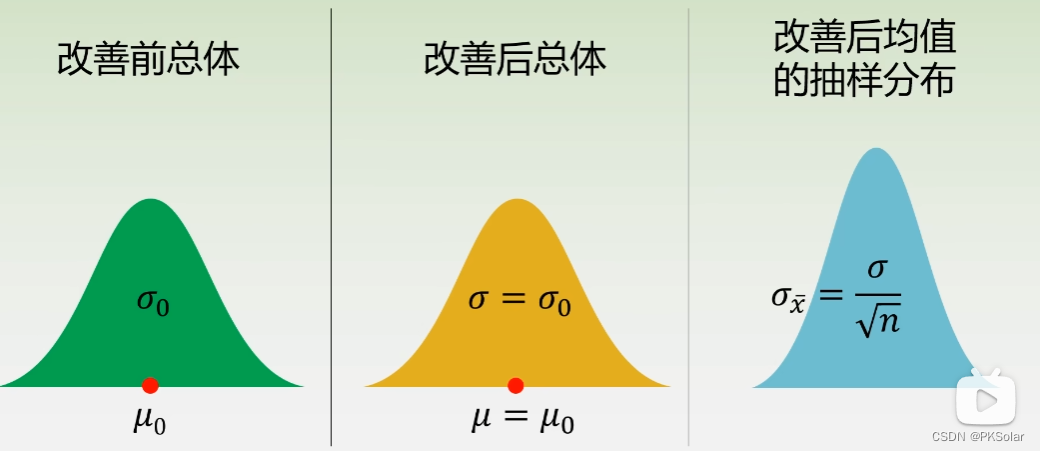
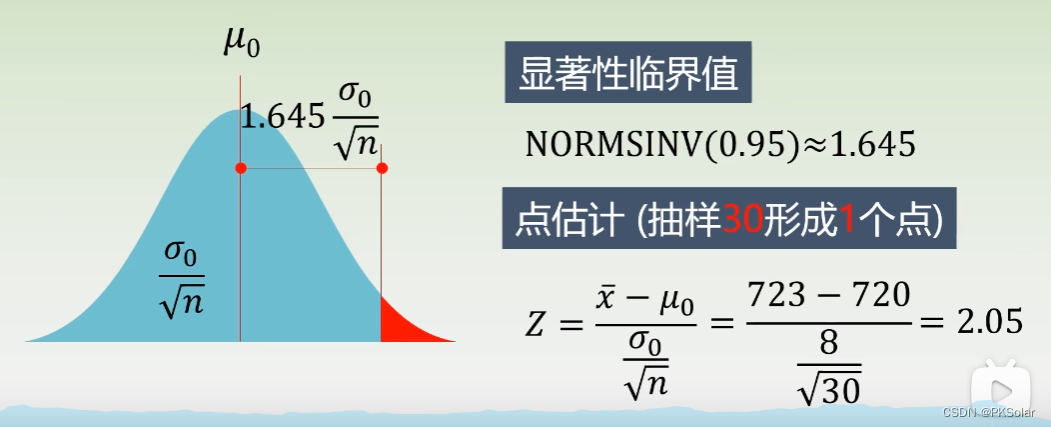
临界值与点估计

对改善前的激光器，其均值和标准差都能算出来，而0.95置信区间也可以计算出（查表或者用Excel，软件）为1.645个标准差的位置。
现在计算抽样得到的改善后激光器的功率，发现其偏差为2.05个标准差的位置。即落在了红色区域，那我可以认为改善后激光器有了显著提升。最终结论：拒绝原假设。功率有明显改善。

什么是P值

上面是用临界值法来判断假设是否成立。
---->计算0.95临界值。计算新样本的偏差是否落在0.05区间。
例如紫色的点都表示，我们不能拒绝原假设，但是力度差别非常大。左边的点非常不能拒绝，右边的点只差一点点。但是这样无法从临界值的计算上得到答案。而P值可以告诉我们检验正确的力度。
抽样30个得到一个平均值m，m落在红色区域时,认为原假设不成立，此时P值可以理解为冤枉原假设的概率（原假设是成立的，但是由于碰巧抽样出现了问题导致抽样得到的m落在了红色区域却认为它是假的，这叫弃真）P值概率越低，则代表抽样出问题的概率越低，越不可能冤枉原假设，就越可能推翻原假设，所以我们需要P值很小。

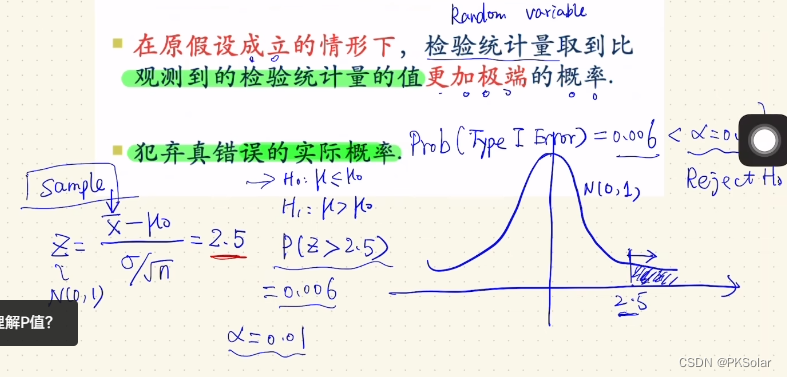
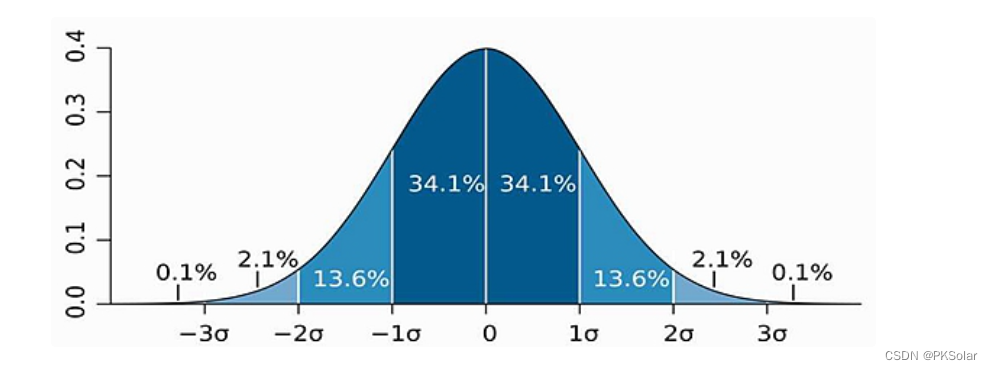
如下图，计算出来Z为2.5，从而计算出，数据落在右边2.5倍标准差的概率为0.006（正态分布的性质，如下图可以看到），因此，此时可以说在显著性水平是0.01 程度上拒绝原假设。

​

参考：
https://www.bilibili.com/video/BV1654y147S9/?spm_id_from=333.337.search-card.all.click&vd_source=fd23946b01c2a9a3f921de79df667850
https://space.bilibili.com/178069433/search/video?keyword=P%E5%80%BC