NGBoost：用于概率预测的自然梯度提升_ngboost: natural gradient boosting for probabilist

1.引言

在此论文中，来自斯坦福的研究者们提出了 NGBoost 梯度提升方法以解决现有梯度提升方法难以处理的通用概率预测中的技术难题。

概率预测（一种模型在整个结果空间中输出完整概率分布的方法）是量化那些不确定性的自然方法。 梯度提升机已经在结构化输入数据的预测任务中取得了广泛的成功，但是对于实际值输出的概率预测，尚没有一种简单的提升解决方案。 NGBoost是一种梯度提升方法，它使用自然梯度（Natural Gradient）来解决现有梯度提升方法难以处理的通用概率预测中的技术难题。这种新提出的方法是模块化的，基础学习器、概率分布和评分标准都可灵活选择。

研究者在多个回归数据集上进行了实验，结果表明 NGBoost 在不确定性估计和传统指标上的预测表现都具备竞争力。

2. 模型

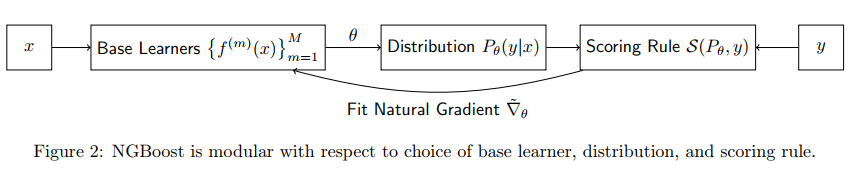
这篇论文提出了自然梯度提升，这是一种用于概率预测的模块化的提升算法，其使用了自然梯度，从而可以灵活地整合不同的以下模块：

• 基础学习器（比如决策树）
• 参数概率分布
• 评分规则（MLE、CRPS 等）

气象学已经将概率式预测用作天气预测的首选方法。在这种设置中，模型会根据观察到的特征输出在整个输出空间上的概率分布。模型的训练目标是通过优化最大似然估计（MLE）或更稳健的连续分级概率评分（CRPS）等评分规则来最大化锐度（sharpness），从而实现校准。这会得到经过校准的不确定度估计。

而梯度提升机（GBM）是一系列能很好地处理结构化输入数据的高度模块化的方法，即使数据集相对较小时也能很好地完成。但是，如果方差被假定为常数，那么这种概率式解释就没什么用处。预测得到的分布需要有至少两个自由度（两个参数），才能有效地体现预测结果的幅度和不确定度。正是这个基础学习器多个参数同时提升的问题使得 GBM 难以处理概率式预测，而 NGBoost 通过使用自然梯度能够解决这个问题。

普通梯度：
$$\nabla \mathcal{S}(\theta ,y)\propto \underset{ϵ\to 0}{\lim }\underset{d:\Vert d\Vert =ϵ}{\mathrm{argmax}}\mathcal{S}(\theta +d,y)$$

自然梯度：
$$\tilde{\nabla }\mathcal{S}(\theta ,y)\propto \underset{ϵ\to 0}{\lim }\underset{ϵ\in {\mathbb{P}}_{\theta }\Vert P_{\theta +d}}{\mathrm{argmax}}\mathcal{S}(\theta +d,y)$$

此外，有
$$\tilde{\nabla }\mathcal{S}(\theta ,y)\propto {\mathcal{I}}_{\mathcal{S}}(\theta {)}^{-1}\nabla \mathcal{S}(\theta ,y)$$

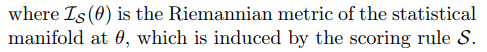
自然梯度特点：
虽然自然梯度最初是用$D_{KL}$诱导的距离度量为统计流形定义的（Martens，2014年），但在此我们提供了一种更通用的方法，适用于与某些适当计分规则相对应的任何差异。 广义自然梯度是黎曼空间中最陡上升的方向，它对参数化是不变的.

对新输入$x$ 的预测 $y|x$ 是以条件分布 $P_{\theta }$ 的形式完成的，其参数 $\theta$ 通过 $M$ 个基础学习器输出（对应于 M 个梯度提升阶段）与一个初始分布 θ(0) 的叠加组合得到。注意 θ 可能是一个参数向量（不限定于标量值），这些参数完全决定了概率预测 $y|x$。为了得到某个$x$ 的预测结果参数 θ，每个基础学习器 f 都以 x 为输入。预测得到的输出使用一个特定于阶段的缩放因子 ρ 和一个通用学习率 η 进行缩放。

$$y|x\sim P_{\theta }(x),\theta ={\theta }^{(0)}-\eta \sum _{m=1}^M{\rho }^{(m)}\cdot f^{(m)}(x)$$

算法：

模型是按序列形式学习的，每个阶段都有一组基础学习器 $f$ 和一个缩放因子 $\rho$。学习算法首先会估计一个共同的初始分布 $\theta (0)$，这样使它能最小化评分规则 S 在所有训练样本的响应变量上的总和，这本质上就是拟合 y 的边际分布。这就变成了所有样本的初始预测参数 $\theta (0)$。

在每次迭代 $m$，对于每个样本 i，算法都会根据该样本直到该阶段的预测结果参数计算评分规则 S 的自然梯度 $g_i$。注意 $g_i$ 和维度与 $\theta$ 一致。该迭代的一组基础学习器 $f$ 将进行拟合，以便预测每个样本 $x_i$ 的自然梯度的对应分量。

拟合后的基础学习器的输出是自然梯度在该基础学习器类别的范围上的投射。然后，通过缩放因子 $\rho$ 对投射后的梯度进行缩放，因为局部近似可能离开当前参数位置后不久就会失效。选取缩放因子的标准是以线搜索的形式最小化沿投射梯度方向的整体真实评分规则损失。

确定了缩放因子之后，再更新每个样本的预测参数。

---

参考：

1. NGBoost: Natural Gradient Boosting for Probabilistic Prediction;
2. 微信公众号 斯坦福吴恩达团队提出NGBoost：用于概率预测的自然梯度提升；