马尔科夫状态转移矩阵

作者：2023面试高手 | 2024-03-26 23:32:28

踩

马尔科夫状态转移矩阵

一、马尔科夫状态转移矩阵性质

1. 每个时间点处在某一个状态，时间是离散的。
2. 每次到下一个时间点时按照图进行随机状态转移。
3. 假如某时的状态是个统计分布（看做向量），那么用状态转移矩阵（权值）乘这个向量就得下一时刻的状态。马尔可夫链的状态数可以是有限的，也可以是无限的。因此可以用于连续概率分布和离散概率分布。

4.Π通常称为马尔可夫链的平稳分布。

二、马尔科夫状态转移矩阵概念

用精确的数学定义来描述，则假设我们的序列状态是...Xt-2,Xt-1,Xt,Xt+1,...,那么我们的在时刻Xt+1的状态条件概率仅仅依赖于时刻Xt,即：

P(Xt+1|...Xt-2,Xt-1,Xt) = P(Xt+1|Xt)

既然某一时刻状态转移的概率只依赖于它的钱一个状态，那么我们只要能求出系统中任意两个状态之间的转换概率，这个马尔科夫链的模型就定了。

三、代码实现：

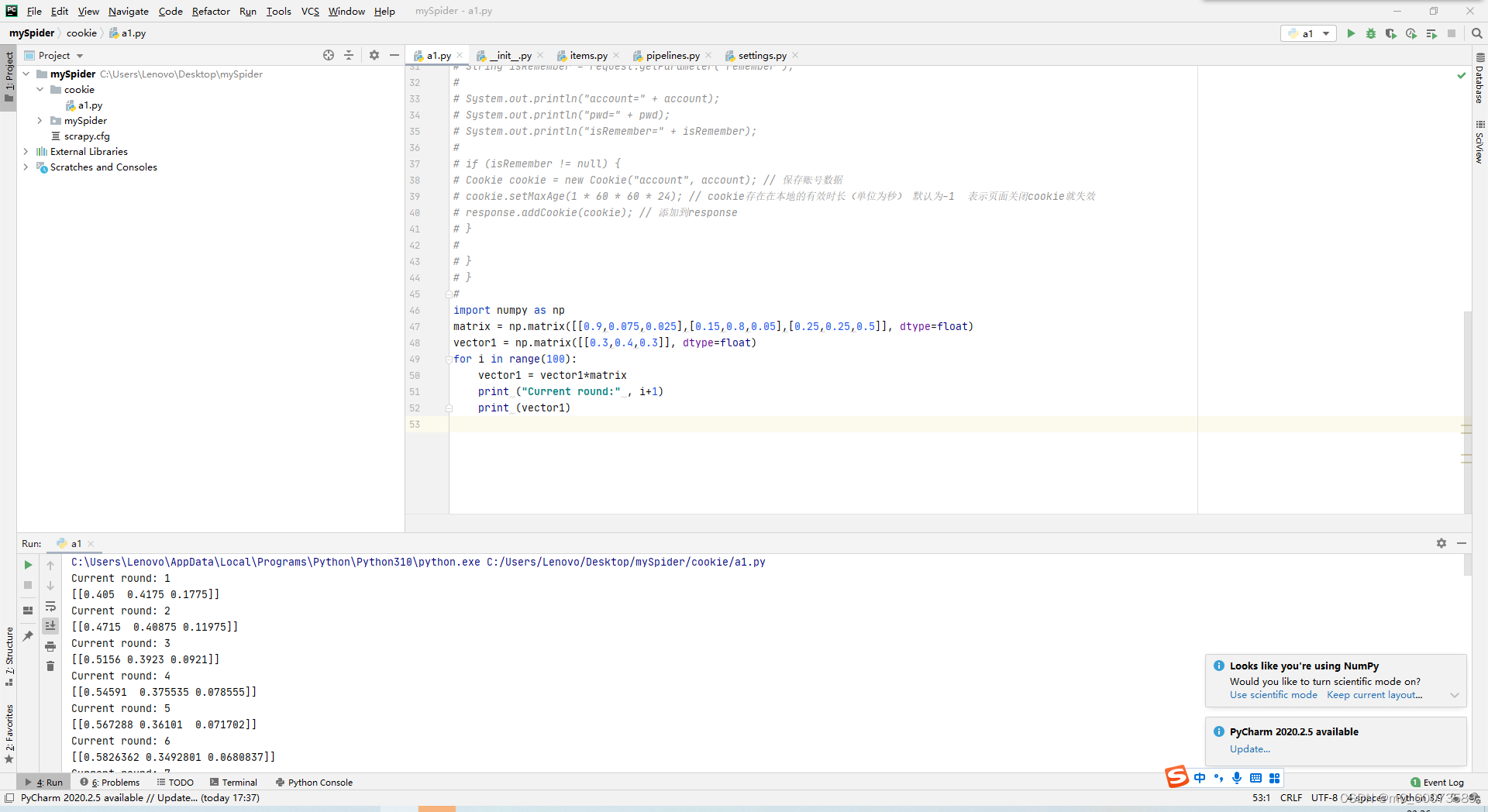
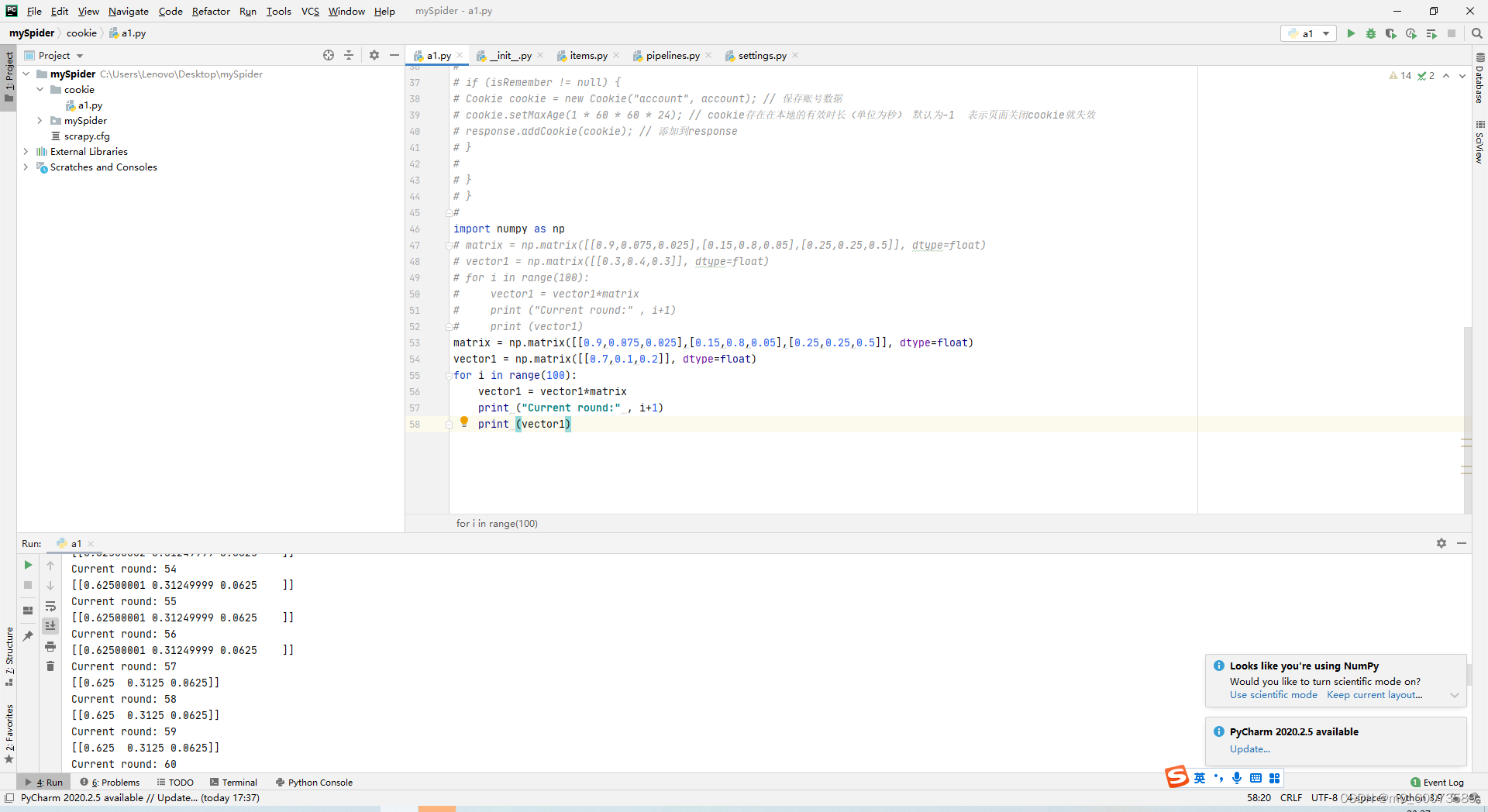
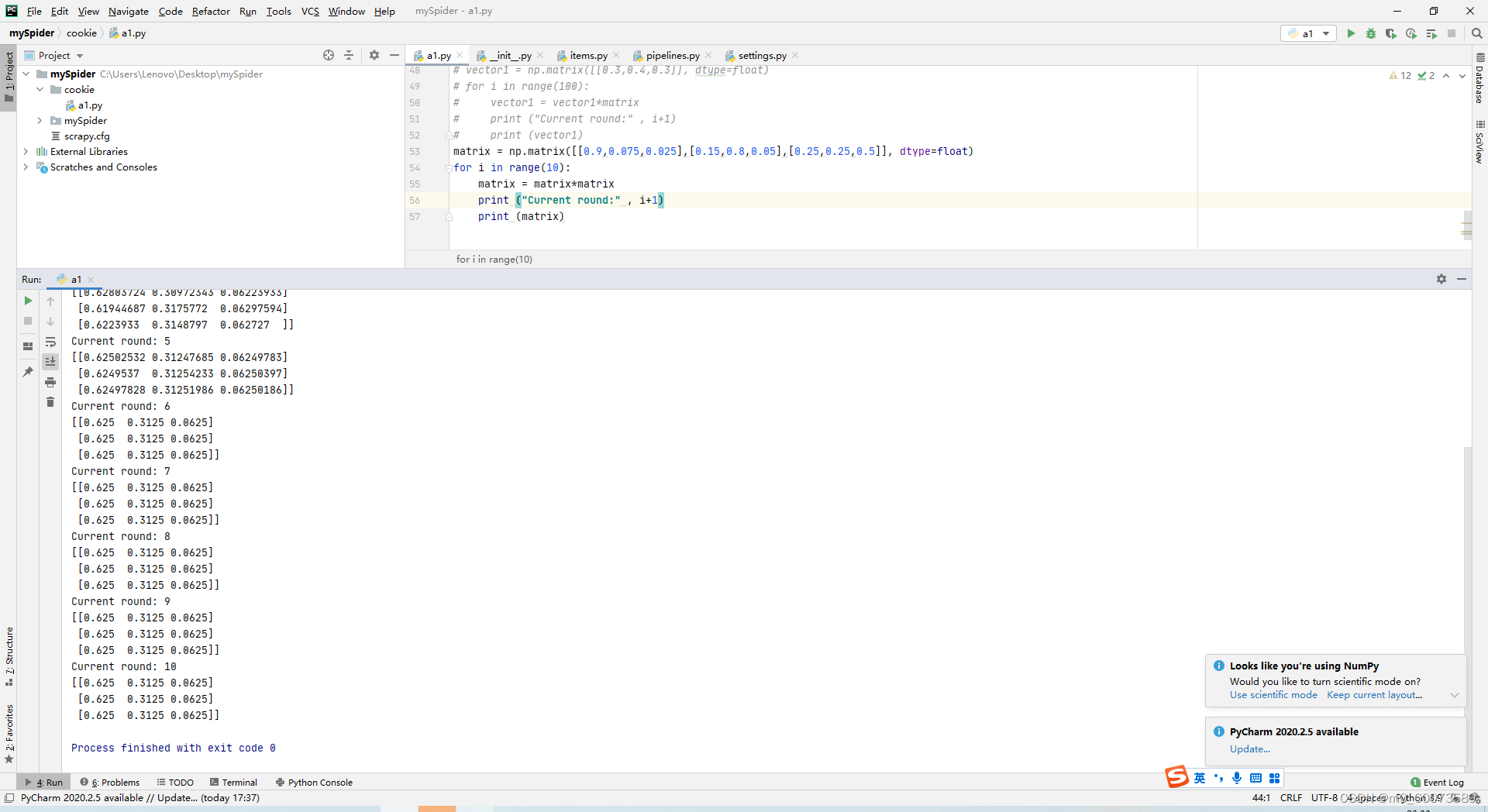
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/2023面试高手/article/detail/320348