- 1CSDN写作模板_csdn博客模板
- 2记录运行SiamMask代码时遇到的问题以及解决方法_modulenotfounderror: no module named 'tools.datase
- 3adb常用指令合集_adb删除文件命令
- 4centos 7.6安装 Apache HTTP Server 2.4.58_apache 2.4.58
- 5基于PaddleServing的串联部署 ocr 识别模型_paddle ocr 部署
- 6MySQL 字符集概念与原理及如何配置字符集 - 超详细图文详解_数据库字符集
- 7人机交互系统(3.1)——NLP文本数据增强方法_dropout 用于文本增强
- 8Ubuntu 20.04安装CUDA失败导致系统黑屏消息nvidia 0000:01:00.0: can‘t change power state from D3cold to D0 的解决方法_can't change power state from d3cold to d0
- 9【自然语言处理六】利用transformer模型实现机器翻译_自然语言翻译模型
- 10计算机专业开题报告案例20: 基于SpringBoot的高校排课系统的设计与实现_fuyuan cheng. talent recruitment management system
C语言实现快速排序算法
赞
踩
1. 什么是快速排序算法
快速排序的核心思想是通过分治法(Divide and Conquer)来实现排序。
算法的基本步骤是:
1. 选择一个基准值(通常是数组中的某个元素),将数组分成两部分,使得左边的部分所有元素都小于基准值,右边的部分所有元素都大于基准值。
2. 对这两部分分别进行递归排序,直到整个数组有序。
那么,该算法为什么叫做快速排序算法呢?
快速排序算法之所以被称为“快速”,是因为它在大多数情况下都能够快速地完成排序。在平均情况下,其时间复杂度为O(nlogn),其中n为数组的大小。
此外,快速排序还具有原地排序的特点,即不需要额外的辅助空间,只需对原始数组进行原地操作。这些优点使得快速排序成为了排序问题中的一种首选算法。
2. 单趟排序
单趟排序指的就是将数组分为两部分的算法。
对于实现这一步,我们有三种思路。
2.1 霍尔法
霍尔并无什么特殊含义,只是因为最早发现快速排序算法的人叫霍尔,这是他的实现方法。
思路:
1. 先选定一个基准值key(一般选择首元素)。
2. 定义两个指针left和right,分别指向数组的左右两端。
3. left从左往右遍历,寻找大于基准值的元素,right从右往左遍历,寻找小于基准值的元素。
4. 如果left与right未相遇,那么就交换两指针指向的元素。
5. 如果left与right相遇,那么就让key指向的元素与right指向的元素交换。
代码
- //霍尔法
- int ParSort_1(int* arr, int left, int right)
- {
- int key = left;
- while (left < right)
- {
- while (left < right && arr[right] >= arr[key]) { right--; }
- while (left < right && arr[left] <= arr[key]) { left++; }
- if (left < right)
- swap(&arr[left], &arr[right]);
- }
-
- swap(&arr[key], &arr[left]);
- return left;
- }
注意事项(如何保证right和left共同指向的元素与key指向的元素交换是合理的)
1. 如果选取的基准值为首元素,那么在外层循环的一次循环中,一定要让right先进行移动,这样可以确保共同指向的元素是小于或等于基准值的。
2. 如果选取的基准值为最后一个元素,则与上面相反。
2.2 挖坑法
核心思想与霍尔法相同,但是表现形式有所差异。
思路
顾名思义,我们将基准值单独用变量进行存放,而将基准值原本所在的位置空出来成为一个坑(我们将其称作hole)。

1. right先进行遍历,如果发现有小于基准值的元素,则将该元素填入hole中,然后right指向的位置成为新的hole。(假设F小于key)

2. 然后left再进行遍历,如果发现有大于基准值的元素,则将该元素填入hole中,然后left指向的位置成为新的hole。(假设B大于key)
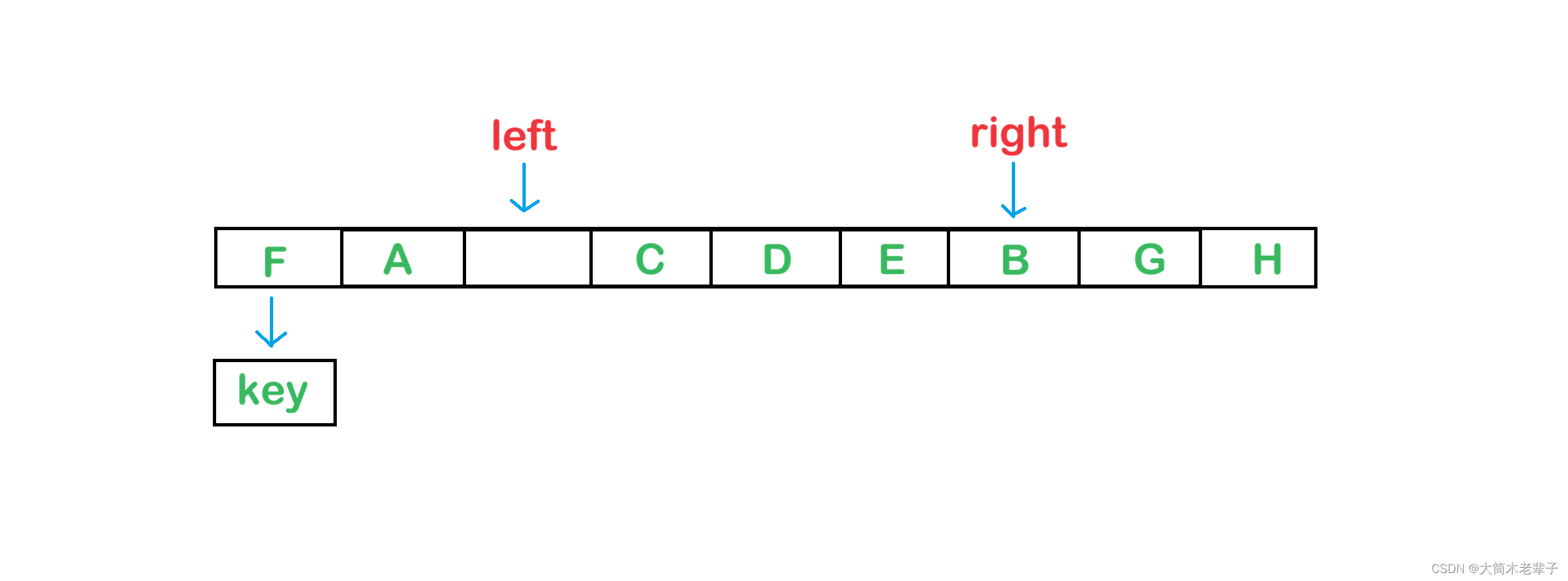
3. 以此类推,当left与right相遇时,将key填入hole中即可。
代码
- //挖坑法
- int ParSort_2(int* arr, int left, int right)
- {
- int key = arr[left];
- int hole = left;
-
- while (left < right)
- {
- while (left < right && arr[right] >= key) { right--; }
- arr[hole] = arr[right];
- hole = right;
-
- while (left < right && arr[left] <= key) { left++; }
- arr[hole] = arr[left];
- hole = left;
- }
-
- arr[hole] = key;
- return hole;
- }

注意事项
对于这个方法来说,洞在谁那边,谁就先开始遍历。
2.3 前后指针法
思路
1. 定义两个指针,prev和cur,prev所指向的以及之前的元素就是小于基准值的元素,cur用于遍历数组。
2. 如果cur找到小于基准值的元素,让prev++,然后交换prev指向的元素和cur指向的元素。
3. 让基准值与prev指向的元素进行交换。
代码
- //前后指针
- int ParSort_3(int* arr, int left, int right)
- {
- int key = left;
- int prev = left;
- int cur = left + 1;
- while (cur <= right)
- {
- //arr[cur]小于基准值就交换
- if (arr[cur] <= arr[key] && ++prev != cur)
- {
- swap(&arr[prev], &arr[cur]);
- }
- cur++;
- }
-
- swap(&arr[key], &arr[prev]);
- return prev;
- }

注意事项
如果选取的基准值为首元素,则在最后让prev指向的元素与基准值交换;如果选区的基准值为最后一个元素,则在最后让prev指向的下一个元素与基准值交换。
3. 快速排序算法的递归实现
按照第一部分的介绍,我们很容易的到下面的代码。
- void QuickSort(int* arr, int begin, int end)
- {
- if (begin >= end)
- return;
-
- int key = ParSort_3(arr, begin, end);
- QuickSort(arr, key + 1, end);//排右边
- QuickSort(arr, begin, key - 1);//排左边
- }
4. 快速排序算法的优化
当数据量十分巨大时,使用递归实现的快速排序算法会由于调用函数次数过多而导致程序效率下降。
由于递归的逻辑结构像是一个树状图,所以在递归的层次较深时,每次进到下一层都会调用上一层两倍数量的函数。
众所周知,是一个极其可怕的东西,那么我们能不能在层次较深,所需排序的数组长度较短时,转而使用其他经典的排序算法呢?
于是我们做出了如下的优化:
- void QuickSort(int* arr, int begin, int end)
- {
- if (begin >= end)
- return;
-
- if (end - begin <= 8)
- {
- InsertSort(arr + begin, end - begin + 1);
- return;
- }
-
- int key = ParSort_3(arr, begin, end);
- QuickSort(arr, key + 1, end);//排右边
- QuickSort(arr, begin, key - 1);//排左边
- }
当数组长度小于等于9时,我们采用插入排序来进行排序(不止插入排序,其他排序也可)。
- //插入排序
- void InsertSort(int* arr, int len)
- {
- for (int i = 1; i < len; i++)
- {
- int j = i;
- while (j > 0 && arr[j] < arr[j - 1])
- {
- swap(&arr[j], &arr[j - 1]);
- j--;
- }
- }
- }
5. 结语
快速排序的非递归算法是用栈模拟递归实现的,由于太麻烦我就没写,感兴趣可以自己尝试写写。
单趟排序算法用哪个,快速排序递归还是非递归,层次较深时换用什么排序算法,这些都是可以自由组合的。


