FFT（快速傅里叶变换）

FFT（快速傅里叶变换）

前言

又要补之前的知识，艹。

快速傅里叶变换 (fast Fourier transform), 即利用计算机计算离散傅里叶变换（DFT)的高效、快速计算方法的统称，简称FFT。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。

也就是说 ：FFT用来加速两个多项式的乘法。

建议学习一下有关复数的知识，这里 我水了一篇博客。

多项式的系数表示法和点值表示法

系数表示法

一个**$n-1$ 次的 $n$ 项**多项式 $f(x)$ 可以表示为 $f(x)={\sum }_{i=0}^{n-1}{a}_i{x}^i$

即：
$$f(x)=a_0+a_1{x}^1+a_2{x}^2+a_3{x}^3+\cdots +a_{n-1}{x}^{n-1}$$
这就是我们平常最常用的 系数表示法

点值表示法

现在有一个多项式 $f(x)$ 我们可以把它在坐标系上表示出来

• 把多项式放到平面直角坐标系里面，看成一个函数

• 把 $n$ 个不同的 $x$ 代入，会得出 $x$ 个不同的 $y$，在坐标系内就是 $n$ 个不同的点

• 那么这 $n$ 个点 唯一确定 该多项式，也就是 有且仅有 一个多项式满足 $∀k, f(x_k) = y_k $ （这个其实跟插值差不多，大家可以看看这个拉格朗日插值法）

所以 $f(x)$ 就可以表示成 $f(x)=(x_0,f(x_0)),(x_1,f(x_1))(x_2,f(x_2)\cdots (x_n-1,f(x_n-1)))$

这就是 点值表示法

高精度乘法下两种多项式表示法的区别

对于两个用系数表示的多项式，我们把它们相乘时。

很明显这个时间复杂度是 $O(n)$ 的

但是点值表示法就不太一样了，只需要 $O(n)$ 的时间。

假设两个点值多项式分别为
$$\begin{gathered} f(x)=(x_0,f(x_0)),(x_1,f(x_1))(x_2,f(x_2)\cdots (x_n-1,f(x_n-1))) \\ g(x)=(x_0,g(x_0)),(x_1,g(x_1))(x_2,g(x_2)\cdots (x_n-1,g(x_n-1))) \end{gathered}$$
设他们的乘积是 $h(x)$ 则
$$h(x)=(x_0,f(x_0)\cdot g(x_0)),(x_1,f(x_1)\cdot g(x_1)),(x_2,f(x_2)\cdot g(x_2)),\cdots (x_n-1,f(x_{n-1})\cdot g(x_{n-1}))$$
所以就只用枚举 $O(n)$ 就够了

好像我们只用把系数表示法转换成点值表示法就可以 $O(n)$ 解决多项式乘法了

朴素系数转点值的算法叫DFT（离散傅里叶变换），点值转系数叫IDFT（离散傅里叶逆变换）

但是我们朴素的系数转点值要 $O(n^2)$ ，所以我们要引入FFT

DFT

建议学习一下有关复数的知识，这里 我水了一篇博客。

对于任意系数多项式转点值，当然可以随便取任意 $n$ 个 $x$ 值代入计算

但是这要 $O(n^2)$ 的时间。

傅里叶 提醒我们，

考虑一下，如果我们代入一些 $x$，使每个 $x$ 的若干次方等于 $1$ ，我们就不用做全部的次方运算了
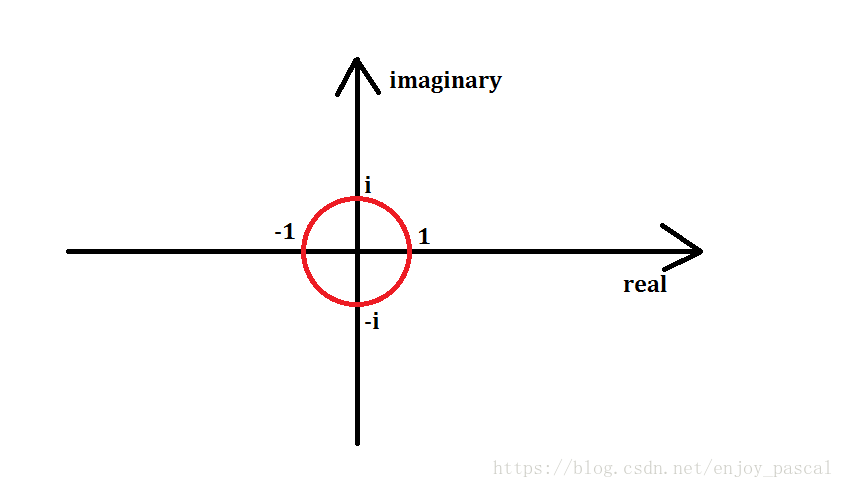
$± 1 $是可以的，考虑虚数的话 $\pm i$ 也可以，但只有这四个数远远不够

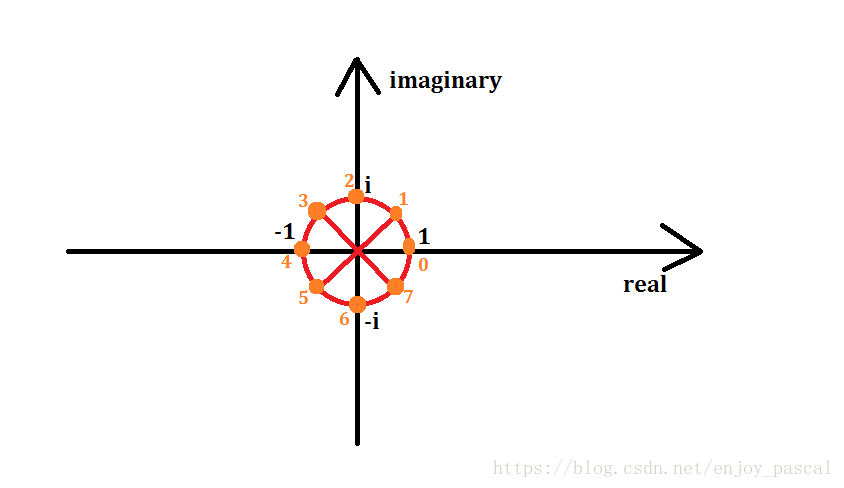
他又说，这个圆上的所有数都可以

以原点为圆心，画一个半径为 $1$ 的单位圆

然后把它 $n$ 等分，如图是 $n=8$

或者说：

图上 $w_n^0,w_n^1,\cdots w_n^{n-1}$ 即为我们要带入的$x_0,x_1,\cdots ,x_n$
$$w_n^k=cos\frac{k}{n}2\pi +isin\frac{k}{n}2\pi$$

单位根的一些性质

1、对任何整数 $n>0,k>0,d>0$ ，有$w_{dn}^{dk}=w_n^k$

2、如果 $nmod2==0$ ：$w_n^{k+\frac{n}{2}}=-w_n^k$

它们表示的点关于原点对称，所表示的复数实部相反，所表示的向量等大反向

3、$w_n^0=w_n^n$

FFT

然后用分治来搞 $DFT$

设：
$$A(x)=\sum _{i=0}^{n-1}{a}_i{x}^i=a_0+a_{1}x+\cdots +a_{n-1}{x}^{n-1}$$
按照 $A(x)$ 下标的 奇偶性 分成两半，右边提出一个 $x$
$$\begin{gathered} A(x)=(a_0+a_2{x}^2+\cdots +a_{n-2}{x}^{n-2})+(a_{1}x+a_3{x}^3+\cdots +a_{n-1}{x}^{n-1}) \\ =(a_0+a_2{x}^2+\cdots +a_{n-2}{x}^{n-2})+x(a_1+a_3{x}^2+\cdots +a_{n-1}{x}^{n-2}) \end{gathered}$$
令：
$$\begin{gathered} A_1(x)=a_0+a_{2}x+a_4{x}^2+\cdots +a_{n-2}{x}^{\frac{n}{2}-1} \\ {A}_2(x)=a_1+a_{3}x+a_5{x}^2+\cdots +a_{n-1}{x}^{\frac{n}{2}-1} \end{gathered}$$
所以：
$$A(x)=A_1(x^2)+x{A}_2(x^2)$$
设 $k<\frac{n}{2}$ ，把 $w_n^k$ 带入 $A(x)$ 得：
$$\begin{gathered} A(w_n^k)=A_1((w_n^k{)}^2)+w_n^k{A}_2((w_{{\frac{n}{2}}^k})) \\ =A_1(w_n^{2k})+w_n^k{A}_2(w_{n}2k)=A_1(w_{\frac{n}{2}}^k)+w_n^k{A}_2(w_{\frac{n}{2}}^k) \end{gathered}$$
带入 $w_n^{k+\frac{n}{2}}$
$$\begin{gathered} A(w_n^{k+\frac{n}{2}})=A_1(w_n^{2k+n})+w_n^{k+\frac{n}{2}}{A}_2(w_n^{2k+n}) \\ =A_1(w_n^{2k})-w_n^k{A}_2(w_n^{2k}{w}_n^n) \\ =A_1(w_n^{2k})-w_k^k{A}_2(w_n^{2k})=A_1(w_{\frac{n}{2}}^k)-w_n^k{A}_2(w_{\frac{n}{2}}^k) \end{gathered}$$
我们发现：$A(w_n^k)$ 和 $A(w_n^{k+\frac{n}{2}})$ 后面的东西只有符号不一样，所以我们可以用 分治 来搞

还要先把 $n$ 补成 $2$ 幂才能搞

IFFT

积的多项式的 点值表达式 然后转成 系数表达式 叫做 $IFFT$

显然：

一个多项式在分治的过程中乘上单位根的共轭复数，分治完的每一项除以n nn即为原多项式的每一项系数

递归版的FFT

#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
#define fd(x , y , z) for(int x = y ; x >= z ; x --)
#define LL long long
using namespace std;
const int N = 4e6 + 5;
const double pi = acos (-1.0);
struct node {
    double x , y;
} a[N] , b[N];
int n , m , len = 1 , r[N] , l;
node operator + (node a, node b) { return (node){a.x + b.x , a.y + b.y};}
node operator - (node a, node b) { return (node){a.x - b.x , a.y - b.y};}
node operator * (node a, node b) { return (node){a.x * b.x - a.y * b.y , a.x * b.y + a.y * b.x};}
int read () {
    int val = 0 , fu = 1;
    char ch = getchar ();
    while (ch < '0' || ch > '9') {
        if (ch == '-') fu = -1;
        ch = getchar ();
    }
    while (ch >= '0' && ch <= '9') {
        val = val * 10 + (ch - '0');
        ch = getchar ();
    }
    return val * fu;
}
void fft (node *A , int inv) {
    for (int i = 0 ; i < len ; i ++)
        if (i < r[i]) 
            swap (A[i] , A[r[i]]);
    for (int mid = 1 ; mid < len ; mid <<= 1) {
        node wn = (node){cos (1.0 * pi / mid) , inv * sin (1.0 * pi / mid)};
        for (int R = mid << 1 , j = 0 ; j < len ; j += R) {
            node w = (node){1 , 0};
            for (int k = 0 ; k < mid ; k ++ , w = w * wn) {
                node x = A[j + k] , y = w * A[j + mid + k];
                A[j + k] = x + y;
                A[j + mid + k] = x - y;
            }
        }
    }
}
int main () {
    n = read () , m = read ();
    fu (i , 0 , n) a[i].x = read ();
    fu (i , 0 , m) b[i].x = read ();
    while (len <= n + m) len <<= 1 , l ++;
    for (int i = 0 ; i < len ; i ++)
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
    fft (a , 1);
    fft (b , 1);
    fu (i , 0 , len) 
        a[i] = a[i] * b[i];
    fft (a , -1);
    // for (int i = 0 ; i <= n + m ; i ++) cout << a[i].x << " " << a[i].y << "\n";
    fu (i , 0 , n + m) 
        printf ("%d " , (int)(a[i].x / len + 0.5));
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

迭代

感性理解一下就好了

#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
using namespace std;
const int N = 4e6 + 5;
const double pi = acos (-1.0);
int n , m1 , m2 , rev[N];
complex<double> a[N] , b[N];
void fft (complex<double> *a , int type) {
    fu (i , 0 , n - 1) 
        if (i < rev[i]) swap (a[i] , a[rev[i]]);
    for (int j = 1 ; j < n ; j <<= 1) {
        complex<double> W(cos (pi / j) , sin (pi / j) * type);
        for (int k = 0 ; k < n ; k += (j << 1)) {
            complex<double> w(1.0 , 0.0);
            fu (i , 0 , j - 1) {
                complex<double> ye , yo;
                ye = a[i + k] , yo = a[i + j + k] * w;
                a[i + k] = ye + yo;
                a[i + k] = ye + yo;
                a[i + j + k] = ye - yo;
                w *= W;
            }
        }
    }
}
int main () {
    scanf ("%d%d" , &m1 , &m2);
    fu (i , 0 , m1) cin >> a[i];
    fu (i , 0 , m2) cin >> b[i];
    n = m1 + m2;
    int t = 0;
    while (n >= (1 << t)) 
        t ++;
    n = (1 << t);
    fu (i , 0 , n - 1) 
        rev[i] = (rev[i >> 1] >> 1) | ((i & 1) ? (n >> 1) : 0);
    fft (a , 1) , fft (b , 1);
    fu (i , 0 , n) 
        a[i] *= b[i];
    fft (a , -1);
    fu (i , 0 , m1 + m2) 
        printf ("%d " , (int)(a[i].real() / (double)n + 0.5));
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

后记

这个讲的好