机器人建模中移动关节如何建立坐标系_工业机器人运动学基本概念

这是自动化圈的第 6 篇文章。

本文介绍的运动学概念，是学习工业机器人的必须清楚的概念。尤其是在处理视觉问题时。运动学主要研究的问题是确定机器人在空间中的位置，只有知道机器人在什么位置，机器人控制柜里的CPU才能去控制机器人。机器人运动学的可分为两个基本问题：正运动和逆运动。正向运动学即给定机器人各关节变量，计算机器人末端的位置姿态；逆向运动学即已知机器人末端的位置姿态，计算机器人对应位置的全部关节变量，逆问题求解比较困难。

自由度

自由度通俗来讲就是描述物体运动的灵活程度，任何一个没有受约束的物体，在空间均具有6个独立的运动。

以上图的长方形为例，它在直角坐标系OXYZ中可以有3个平移运动和3个转动。3个平移运动分别是沿X,Y,Z轴的平移运动,3个转动分别是绕X,Y,Z轴的转动。习惯上把上述6个独立运动称做6个自由度。

如上图，六轴工业机器人一般有6个自由度，常见的六轴工业机器人包含旋转（S轴），下臂（L轴）、上臂（U轴）、手腕旋转（R轴）、手腕摆动（B轴）和手腕回转（T轴）。

位姿

位姿用来描述空间中某个物体的位置和方位，位置通常使用坐标（x,y,z）描述，方位使用(Rx,Ry,Rz)描述，即绕x,y,z轴倾斜的角度。因此，通过（x,y,z,Rx,Ry,Rz)就可以确定机器人在空间任意位置的姿态。

坐标系

工业机器人常见坐标系通常有：基座标系，大地坐标系，工具坐标系，工件坐标系（用户坐标系）、关节坐标系等。

基坐标系，顾名思义是根据机器人基座建立的直角坐标系，大地坐标系是以相对静止的大地为参考，有时候机器人基座是固定在大地上的，那基座标系和大地坐标系重合，如果机器人基座如上图一样是移动的，那基坐标系和大地坐标系是两个不同的坐标系。

工具坐标系是机器人手腕法兰盘安装的工具的有效方向作为z轴，建立的直角坐标系。

工件坐标系：也成为用户坐标系，是用户自己的定义的XYZ直角坐标。当工件的形状是倾斜的时候，建立用户坐标系，调试起来会比较方便。

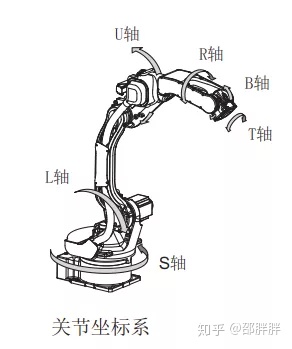
关节坐标使机器人各轴单独运动，称为关节坐标系

空间方位

前面通过坐标系可以确定机器人在空间中的位置（x,y,z）,那么确定机器人的角度旋转通常有RPY角和欧拉角表达方式。他们区别是RPY角是绕定轴旋转，欧拉角是绕自身的轴旋转（动轴旋转）。

RYP角

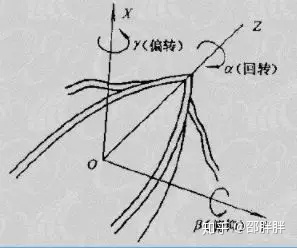
RPY角是描述船舶在海中航行时姿态的一种方法。

Roll：将船舶的行驶方向取为z轴，则绕z轴的旋转(α角)称为滚动；

Pitch：把绕Y轴的旋转(β角)称为俯仰；

Yaw：把垂直方向取为X轴，绕X轴的旋转（γ角）称为偏转；

z-y-x欧拉角

初始状态时，运动坐标系的初始方位与参考系相同，当开始运动时，首先使运动系Z轴转α角，然后绕运动系的Y轴转β角，最后绕运动系的X轴转γ角。

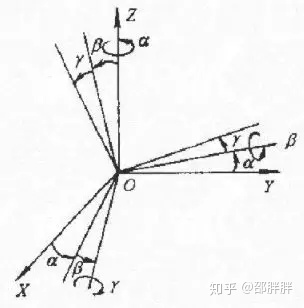
欧拉角是表达旋转的一种简单方法，由三个角度组成，其值分别代表物体绕坐标系的三个轴（x, y, z轴）的旋转角度，不同的旋转顺序会有不同的旋转结果。这种描述中的各次转动都是相对于运动坐标系的某轴进行的，而不是相对于固定的参考系，这就是动轴旋转。