蓝桥杯最短路（java实现）

作者：2023面试高手 | 2024-04-24 19:05:33

踩

蓝桥杯最短路（java实现）

题目

资源限制

内存限制：256.0MB Java时间限制：3.0s

问题描述

给定一个n个顶点，m条边的有向图（其中某些边权可能为负，但保证没有负环）。请你计算从1号点到其他点的最短路（顶点从1到n编号）。

输入格式

第一行两个整数n, m。接下来的m行，每行有三个整数u, v, l，表示u到v有一条长度为l的边。

输出格式

共n-1行，第i行表示1号点到i+1号点的最短路。

样例输入

3 3

1 2 -1

2 3 -1

3 1 2

样例输出

-1

-2

数据规模与约定

对于10%的数据，n = 2，m = 2。

对于30%的数据，n <= 5，m <= 10。

对于100%的数据，1 <= n <= 20000，1 <= m <= 200000，-10000 <= l <= 10000，保证从任意顶点都能到达其他所有顶点。

代码

Ⅰ.Dijkstra算法


import java.util.Scanner;
 
public class Main {
    //不能设置为Integer.MAX_VALUE，否则Integer.MAX_VALUE相加会溢出导致出现负权
    public static int INF = 0x3f3f3f3f;
    
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt(); //顶点数
        int m = in.nextInt();  //边数
        int[][] len = new int[n+1][n+1];
        //初始化邻接矩阵
        for (int i = 1; i < n+1; i++) {
            for (int j = 1; j < n+1; j++) {
                len[i][j] = INF;
            }
        }
        for (int i = 0; i < m; i++) {
            int u = in.nextInt();
            int v = in.nextInt();
            int l = in.nextInt();
            len[u][v] = l;
        } 
        int source = 1; //源点为1
        dijstra(len, 1);//调用dijstra算法计算最短路径
    }
    
    public static void dijstra(int[][] len, int source) {
        //最短路径长度
        int[] shortest = new int[len.length];
        //判断该点的最短路径是否求出
        int[] visited = new int[len.length];
        //存储输出路径
        String[] path = new String[len.length];
        //初始化出发节点
        shortest[source] = 0; //设置出发结点的访问距离为0
        visited[source] = 1;  //设置出发节点被访问过
 
        for (int i = 2; i < len.length; i++) {
            int min = INF;
            int index = -1;
            for (int j = 2; j < len.length; j++) {
                //已经求出最短路径的节点visit[j]==1排除在外无需判断
                if (visited[j] == 0 && len[source][j] < min) {
                    min = len[source][j];
                    index = j;
                }
            }
            //更新最短路径
            shortest[index] = min;
            visited[index] = 1;
            //更新从index跳到其它节点的较短路径
            for (int m = 1; m < len.length; m++) {
                if (visited[m] == 0 && len[source][index] + len[index][m] < len[source][m]) {
                    len[source][m] = len[source][index] + len[index][m];
                }
            }
 
        }
 
        //打印最短路径
        for (int i = 2; i < len.length; i++) {
            System.out.println(shortest[i]);
        }
    }
}

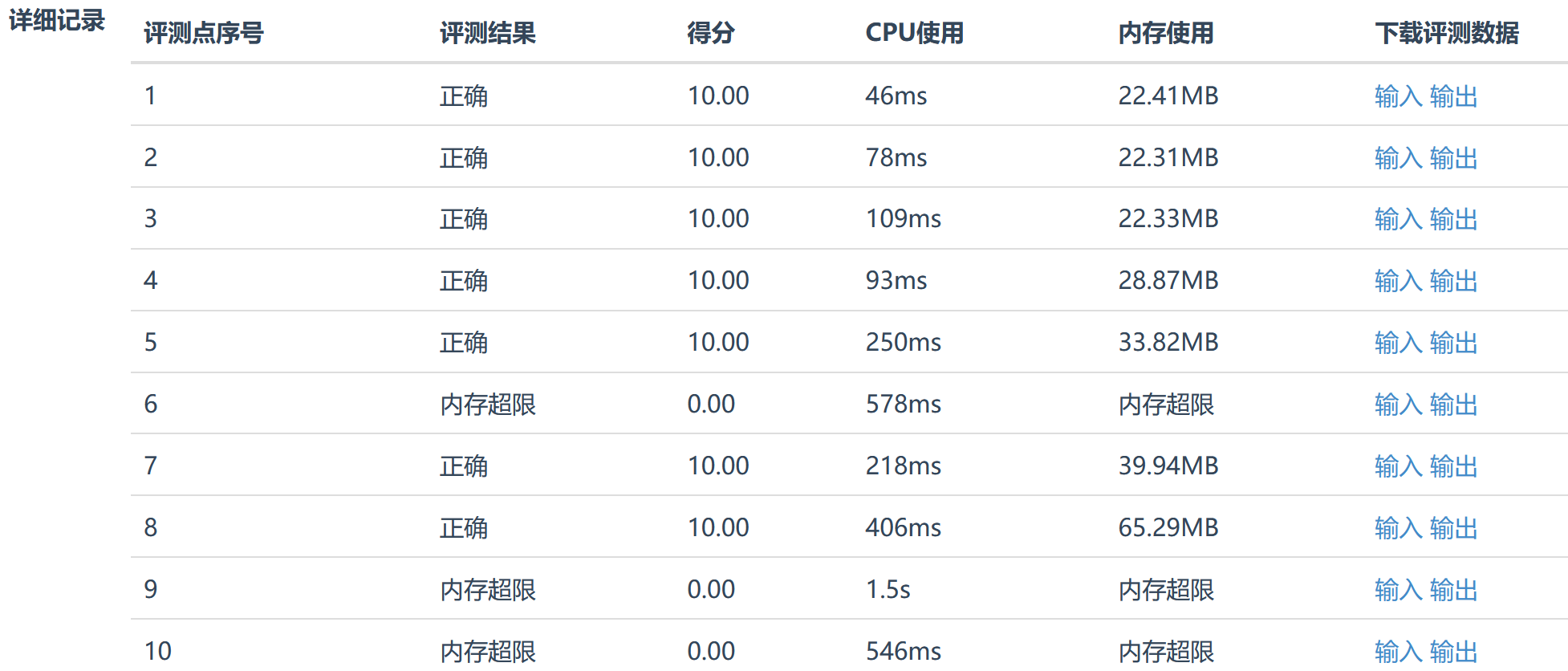
可以看到，使用Dijkstra算法不能通过所有数据。本题也不推荐使用Dijkstra算法来解决。因为题目提到有向图的部分边可能为负权，而Dijkstra算法并不能很好的解决有负权的图。

注意到代码中有public static int INF = 0x3f3f3f3f; 我们经常需要设置一个常量用来代表"无穷大"。比如对于int类型的数，有的人会采用INT_MAX，即0x7fffffff作为无穷大。但是以INT_MAX为无穷大常常面临一个问题，即加一个其他的数会溢出。所以我们常采用0x3f3f3f3f来作为无穷大。

使用INF=0x3f3f3f3f的好处：
1. 0x3f3f3f3f的十进制为1061109567，和INT_MAX一个数量级，即10^9数量级，而一般场合下的数据都是小于10^9的。
2. 0x3f3f3f3f * 2 = 2122219134，无穷大相加依然不会溢出。
3. 可以使用memset(array, 0x3f, sizeof(array))来为数组设初值为0x3f3f3f3f，因为这个数的每个字节都是0x3f。 memset是按字节来memset的，int有四个字节，就会把每个字节都变成0x3f。一般要么memset成0，要么memset成-1，因为int 型 0每个字节都是0，-1每个字节都是-1.

Ⅱ. Bellman-ford算法


import java.util.Arrays;
import java.util.Scanner;
 
public class Main {
    static int INF = 0x3f3f3f3f;
    
    public static void main(String[] args) {    
        Scanner in = new Scanner(System.in);
        int n = in.nextInt(); //n个顶点
        int m = in.nextInt();  //m条边
        //使用邻接矩阵来存储数据
        int[][] len = new int[n+1][n+1];
        //初始化邻接矩阵
        for (int i = 1; i < n+1; i++) {
            for (int j = 1; j < n+1; j++) {
                len[i][j] = i == j ? 0 : INF; 
            }
        }
        for (int i = 0; i < m; i++) {
            int u = in.nextInt();
            int v = in.nextInt();
            int l = in.nextInt();
            len[u][v] = l;
        } 
        int source = 1; //源点为1
        getShortPaths(len,source,n); //调用函数求出最短距离
    }
 
    //返回第1个顶点到其它所有顶点之间的最短距离
    public static void getShortPaths(int[][] len, int source, int n) {
        int[] dist = new int[n+1]; //数组dist，存储最短距离
        Arrays.fill(dist, INF); //初始化数组dist[]
        dist[source] = 0; //令出发的dist[]为0，即dist[1]为0
        for (int limit = 0; limit < n-1; limit++) {
            int[] clone = dist.clone(); //对dist[]进行备份
            for (int i = 1; i < n+1; i++) {
                for (int j = 1; j < n+1; j++) {
                    //松弛操作使用了从 i 到 j 的当前最短距离来更新 dist[j]
                    //注意在迭代时使用备份clone[i]来进行更新操作
                    dist[j] = Math.min(dist[j], clone[i] + len[i][j]);
                }
            }
        }
        //打印最短路径
        for (int i = 2; i < n+1; i++) {
            System.out.println(dist[i]);
        }
    }
}

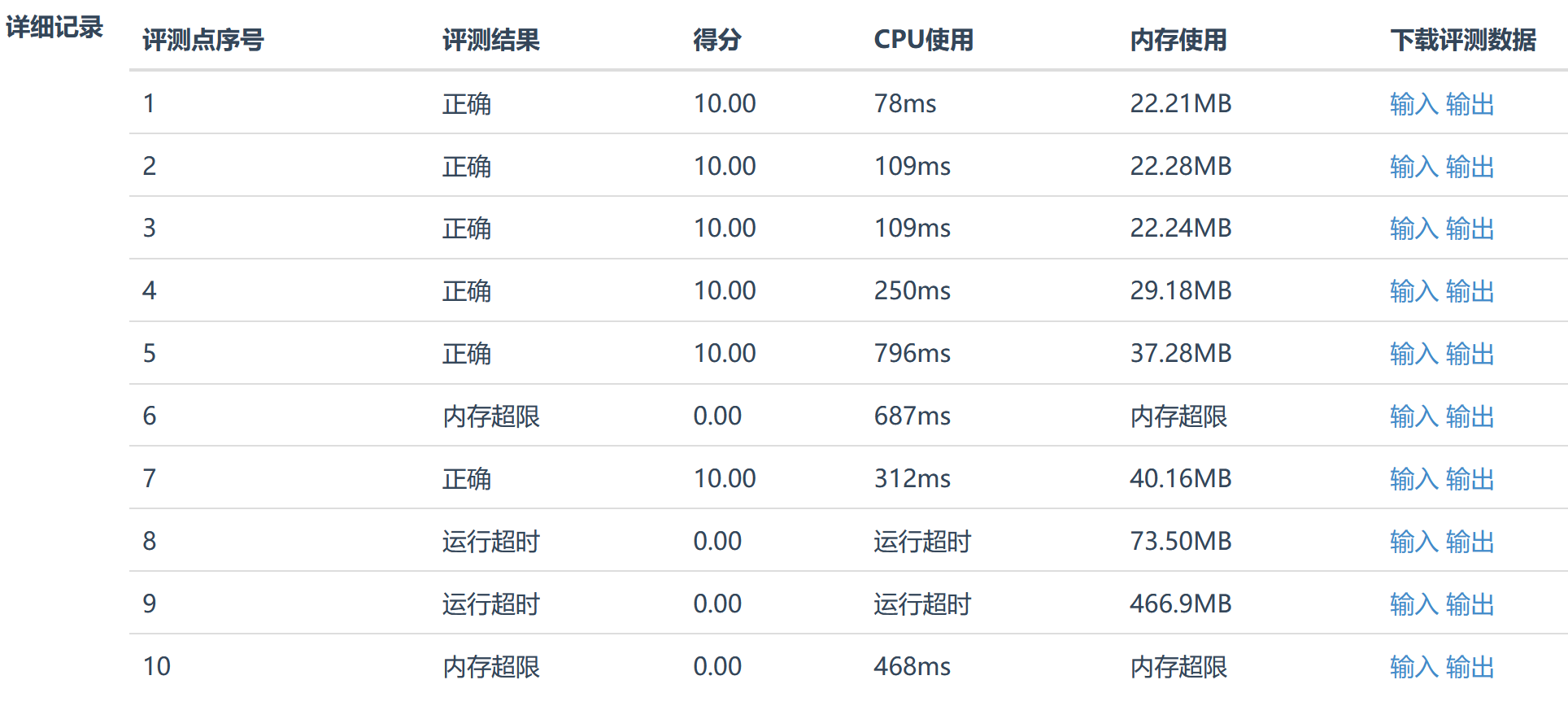
Dijkstra算法不能解决带有负权边的问题，而Bellman-ford算法可以解决带有负权边的问题，是求解带负权边的单源最短路问题的经典算法。但本题用Bellman-ford算法也无法通过是因为其通过遍历所有的边来找到最短路径，对于数据量大的测试而言容易造成内存超限和运行超时。

需要注意的是，在遍历所有的“点对/边”进行松弛操作前，需要先对 dist 进行备份，否则会出现「本次松弛操作所使用到的边，也是在同一次迭代所更新的」，从而不满足边数限制的要求。举个
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/2023面试高手/article/detail/481093