详解多种动态规划问题，看完必会动态规划

基本概念

动态规划（Dynamic Programming，简称DP）是运筹学的一个分支，是求解决策过程最优化的过程。20世纪50年代初，美国数学家贝尔曼等人在研究多阶段决策过程的优化问题时，提出并创立。

理解认知

动态规划(DP)通过循环做出每一步的最优解从而自底向上的得出对问题的整体最优解；这是它与分支算法的自顶向下求解和与贪心算法寻找局部最优解有本质的区别。

接下来为大家说明三步骤通解动态规划问题

动态规划解题模式

确定定义 —> 找初始值 —> 思考关系 =>写代码解

只要掌握这几步必会动态规划任意题型，本文提供多种动态规划题型按此模板解析，话不多说开始例题实战。

基础题型

一、青蛙跳台阶

问题：一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。
1
2
3

输入输出示例，下面给出三次 单独的 各自输入输出；

n=2时有2种跳法，n=7时有21种跳法，n=2时有1种跳法

输入：n = 2   |  n = 7  |   n = 0
输出：2       |  21     |   1
1
2

确定定义

这里要求跳上n级的台阶有多少种方法，就设dp[n]为跳上n级的台阶的跳法数

找初始值

动态规划是自底向上解决问题的，所以底部最小单元的初始值是必须明确的，这里我们可以看到上面示例中第三组输入n为0时输出为1（台阶为0级时只有一种跳法）；而一级台阶只有一种跳法，两个台阶有两种跳法(1+1/2)，三个台阶有三种跳法(1+1+1/1+2/2+1)…

显而易见初始值为n=0和n=1和2时情况

即为dp[0]=1，dp[1]=1，dp[2]=2

思考关系

上面提到过动态规划通过循环做出每一步的最优解从而自底向上的得出对问题的整体最优解，循环每一步就是依靠每个单元的关系依次推到，由dp[0]靠关系推导到dp[1]，由dp[1]推导dp[2]…接下来推导出最终要求的 dp[n] 即为解决问题

这里的n阶台阶方法数推导之间有什么关系？

抛开初始值n=0和n=1，这里稍微思考一下其中关系
台阶数     跳法                    跳法数
n=2       11 2                    2

n=3       111 12 21               3

n=4       1111 112 121 211 22     5
1
2
3
4
5
6
7

我们思考一下要跳到一个n级台阶，其最后一步只能在跳一步或两步的方式

这里可以分类

台阶数     最后跳一步的跳法    最后跳两步的跳法    总跳法数
n=2       11               2                 1+1=2         
 
n=3       111 21           12                2+1=3

n=4       1111 121 211     112 22            3+2=5       
1
2
3
4
5
6

总跳法=最后跳一步的跳法数 + 最后跳两步的跳法数

关系方程就出来了

dp[n]=d[n-1]+d[n-2]

---

因为本题本质是求斐波那契数列的变体解问题

d[0]=1; d[1]=1; d[2]=2; d[3]=3; d[4]=5

1 1 2 3 5

这里数学基础扎实的读者可以看出从dp[1]开始就是斐波那契数列（2=1+1；3=1+2；5=2+3），继而快速推导出公式

d[n] = d[n-1] + d[n-2] ，这是累计经验更快更准确分析分题，多刷题和思考也能到这样

写代码解

完成上三步骤后代码解法就很显而易见了，因为解题本质是从题型中分析并确定需要的算法思想，在将其以代码形式表达出来的过程

这里上代码和注释

class Solution {
    public int numWays(int n) {
        int[] dp = new int[Math.max(n+1, 3)];
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 2;
        for(int i = 3; i<= n; i++){
            dp[i] = (dp[i-1]+dp[i-2]) % 1000000007;  //对1000000007取余是题干要求
        }
        return dp[n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

二、连续子数组的最大和

输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。

要求时间复杂度为O(n)。

【示例】
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
1
2
3
4
5
6
7
8

确定定义

本题问题是找出数组和的最大值，那就设最后要返回的最大值为 int max（值为最大和的子数组）

动态规划是自底向上不断循环每一步的最优解来使得全局最优，全局最优解max已经有了

再设出每一步的局部最优解 int dp（值为每次循环中求得的最大数组）

比如要求你三天吃饭用时最大的三餐时间之和max；那么 dp[n] 为你第n天里三顿中用时最长的一顿早/中/晚饭，

max = dp[1] + dp[2] +dp[3]
1
2
3

清楚明白，定义完成

找初始值

如果是找数组/字符规律那初始值就从最开始的0，1，2套入，然后发现其中特殊的的值

但这里是求已知数组的最大值，而且已经定义好了max和dp，直接将0赋予作为初始值

int dp = nums[0];
int max = nums[0];
1
2

清楚明白，已经找好

思考关系

tip:有小伙伴可能想出想要 子数组和最大，其第一个和最后一个都一定是正数；毕竟开场和结尾可以选择的正数来最大化数组和，但要思考到 [-1] [-1,-2,-3] 这种示例，所以找首尾一定是正数的思维是在这里行不通的。

数组和是由每一个单个的数字环环相扣连接累加而成（理解这句“废话“才能动态规划求最优解）

一个子数组m加上紧接的下一个数字m的值，m+n>n,那铁定把收编到数组里，但如果m+n<n; 那m数组还成了负担，不如重新让数字n替换为新的数组

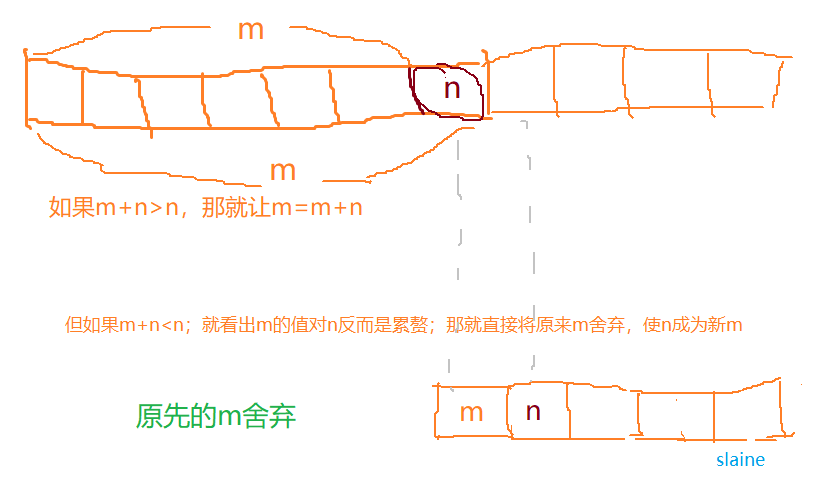
下举例中m和n都是随机设，主要是表示出这个道理

{3，1，-2}中m为{3+1=4}时，n为-2；m+n>n，所以收编n后新数组m为{3,1,-2}

{-6,2,-1}中m为{-6+2=-4}，n为-1；m+n<n，m数组值这么小反而成了累赘，所以令m=n，即m新设为{-1}

将想清楚这种数组的最大构成关系后，就能模拟出关系表达式了

dp = Math.max{ dp + num[i]，num[i]}

(第一个max为定义的最大值变量，第二个为 Math.max 是比较并选取两数中较大的一个)

写代码解

package slaine;

public class test {
    public static void main(String[] args) {
        int[] nums = {-2,1,-3,4,-1,2,1,-5,4};
        System.out.println(maxSubArray(nums));
    }
    public static int maxSubArray(int[] nums) {

        int dp = nums[0];
        int max = nums[0];

        for(int i = 1; i < nums.length; i++){
//            System.out.println("传入数组第"+i+"个数字是"+nums[i]);
            dp = Math.max(dp + nums[i], nums[i]);
//            System.out.println("dp选取为"+dp);
            max = Math.max(max, dp);
//            System.out.println("第"+i+"次循环中最大值为"+max);
            System.out.println();
        }
        return max;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

进阶题型

现在我们开始加速了小伙伴们，冲冲冲，这里选的 “礼物的最大价值” 是刚我们做过的 “连续子数组的最大和” 进阶小变体

三、礼物的最大价值

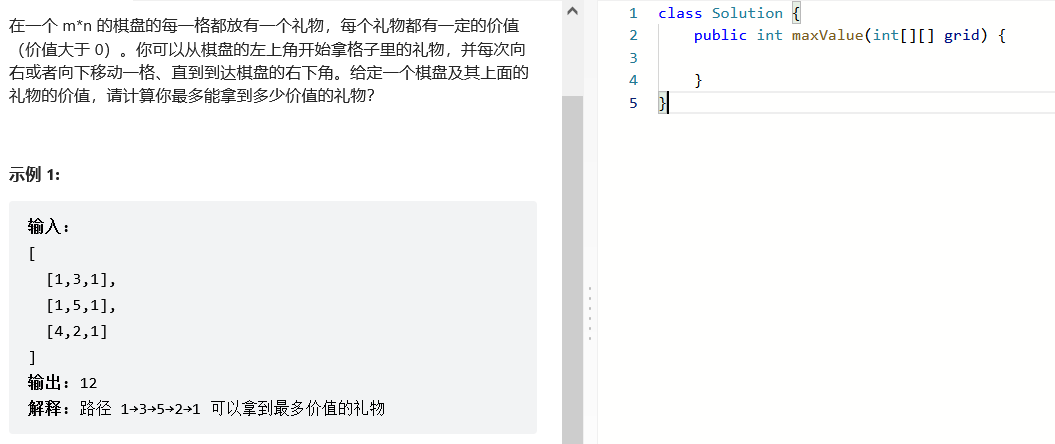
很显然本题将 “求连续数组最大和”的一维数组变体为 求二位数组中路径最大值，乍一看有点难搞？不要怕，照样三步骤轻松拆解

确定定义

注意传入的二维数组为 int[][] [] [] grid；

新建一个n行m列的与输入同格式二维数组 int [] []dp

int n = grid.length;

int m = grid[0].length;

int[][] dp = new int[n][m];
1
2
3
4
5

但新建的二维数组dp里要装什么？动动你的小脑袋想想，

【动态规划通过循环做出每一步的最优解从而自底向上的得出对问题的整体最优解】（这句话在本文至少出现三遍…）,

那当然显而易见的新建二维数组dp其中 每个元素 是当前循环中的想求的最优解

看不懂上面这句话的笨蛋 在本文 Ctrl+F 搜索 “吃饭” ，背下例子并把【】的话背三十遍

为了更清楚的解释我们建的dp数组要装什么玩意，这里举例（作者S1aine真的殚心竭虑地想给你说明白）

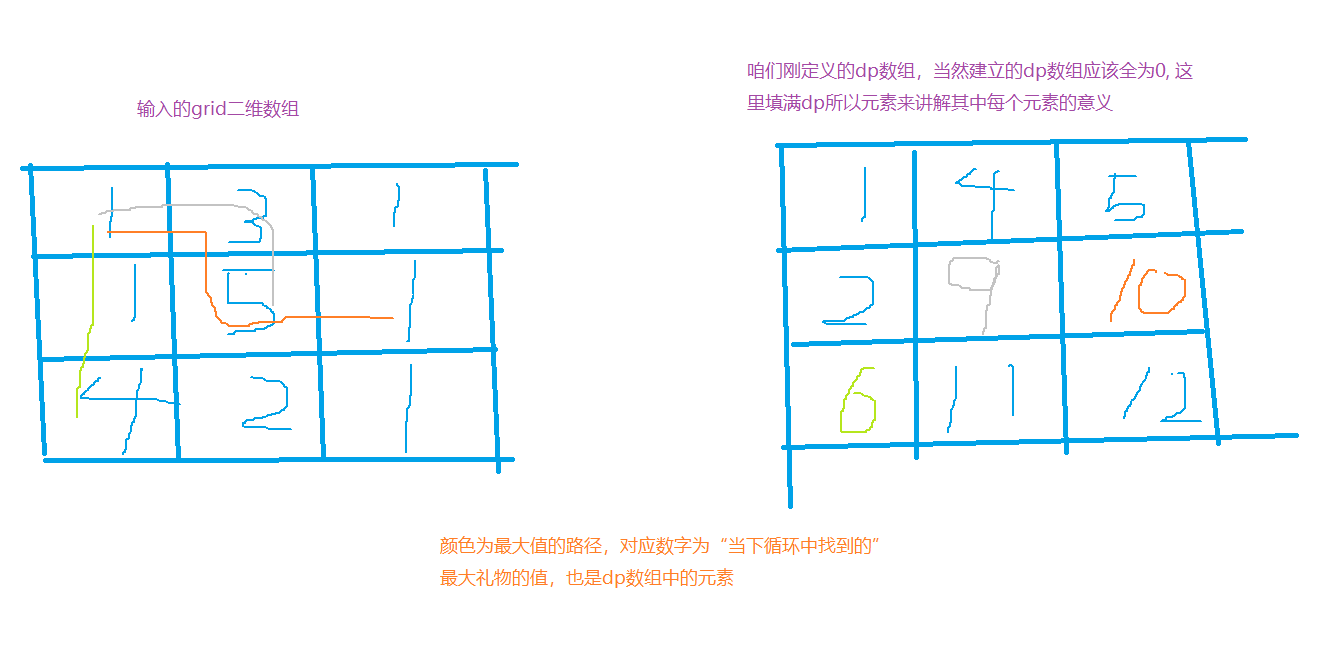
输入二维数组int [] [] grid: 
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]

那么我们新建的二维数组dp就应该是
[
  [1,4,5],
  [2,9,10],
  [6,11,12]
]
1
2
3
4
5
6
7
8
9
10
11
12
13

找初始值

回忆一下刚才咱们在 “连续子数组的最大和” 里怎么定义初始值的？直接把初值第0个赋予了max和dp[i]

这里的初值什么？ 第一反应是左上角的grid[0] [0] ，将它作为初始值赋予dp[0] [0]没有问题

但是同时要结合题干考虑，题干里明确说了每次只能 “向右 或者 向下” 走，那就明显还需要边界的初始值来约束路径

那边界初始值自然是dp中第0行和第0列了，求第0行和第0列两串初始值

        int n = grid.length;
        int m = grid[0].length;

        int[][] dp = new int[n][m]; //左上角初始值
        dp[0][0] = grid[0][0];
        for(int i = 1; i < n; i++){  //第0列的初始值
            dp[i][0] = dp[i-1][0] + grid[i][0];
        }
        for(int j = 1; j < m; j++){ //第0行的初始值
            dp[0][j] = dp[0][j -1] + grid[0][j];
        }
1
2
3
4
5
6
7
8
9
10
11

初始值全部找到，下一个步骤

思考关系

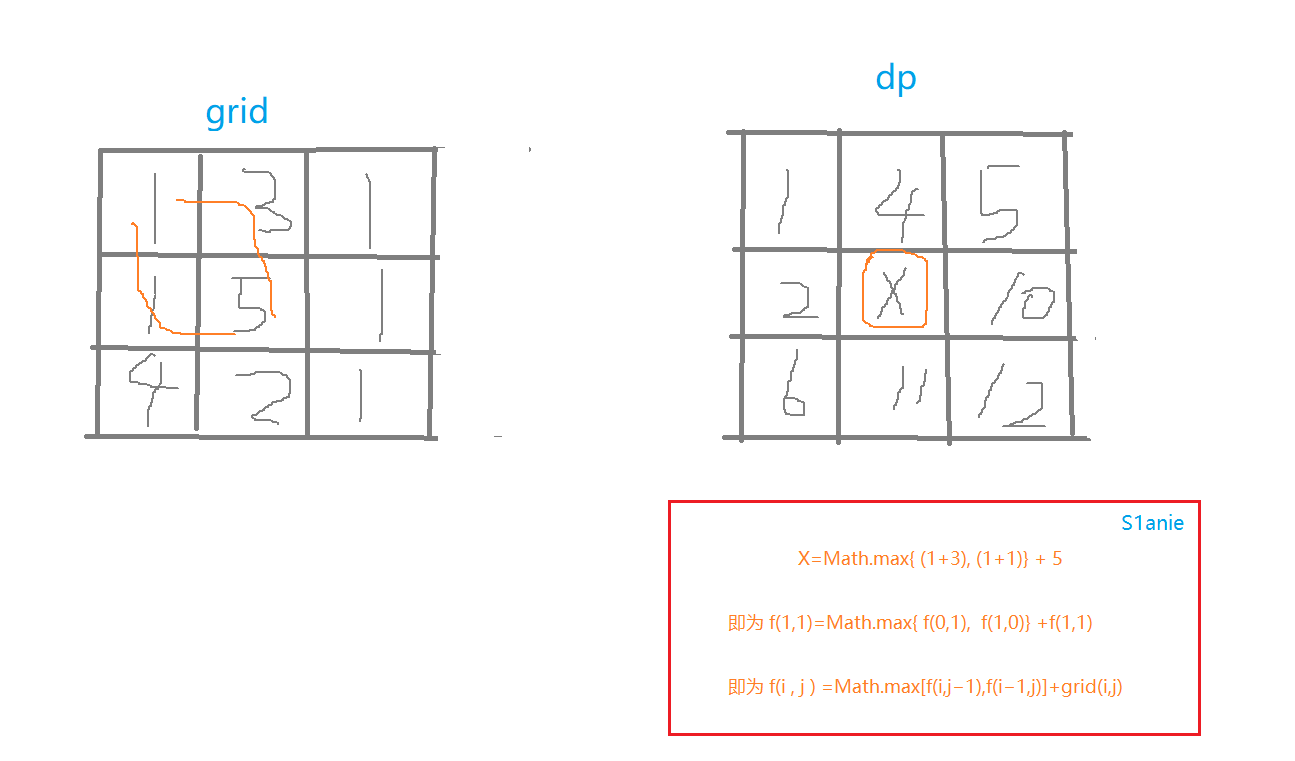
这里直接引用 Krahets 总结好的公式，感谢K佬

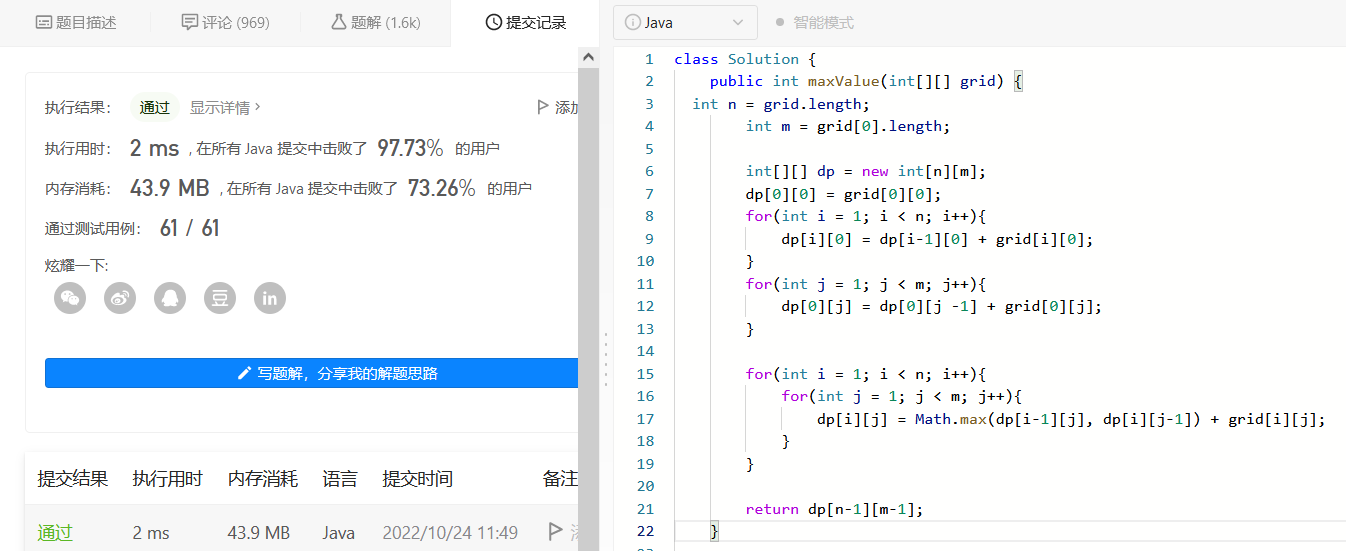
写代码解

class Solution {
    public int maxValue(int[][] grid) {

        int n = grid.length;
        int m = grid[0].length;

        int[][] dp = new int[n][m];
        dp[0][0] = grid[0][0];
        for(int i = 1; i < n; i++){
            dp[i][0] = dp[i-1][0] + grid[i][0];
        }
        for(int j = 1; j < m; j++){
            dp[0][j] = dp[0][j -1] + grid[0][j];
        }

        for(int i = 1; i < n; i++){ 
            for(int j = 1; j < m; j++){
                dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]) + grid[i][j];
            }
        }

        return dp[n-1][m-1];
    }
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

四、机器人的运动范围

还等着看题解？

都学了这么多了不去练练？

与上题同样是二维数组的动态规划但做了些小变体

点击下方传送门开始手撕

机器人的运动范围

加油哦, ~ ~ ~