【python】scikit-learn包：机器学习_accuracy_score是哪个包

环境配置：Scikit-learn包

只支持python语言

安装

Win+R ，输入指令：pip install -U scikit-learn

Part 0. 数据预处理

数据导入

借助pandas和numpy 进行数据导入与处理

字符串类label的数字化编码

机器学习的函数大部分只能对数字信息进行处理，无法对string类数据进行分析，因此需要将string类信息进行编码数字化
参考blog链接，可进行补码

Part 1. 机器学习之线性回归

问题描述

给定数据集 [x1,x2,x3,…,y]，拟合y与各个因子之间的关系

内部算法的原理概述

求到最合适的y=a*x+b，使得偏差最小；即寻找a,b，使得偏差函数dif(a,b)取最小值
拟合原理：在偏差函数上，基于 “模拟退火” 算法，对a，b进行求解。

单因子拟合

求解线性方程

from sklearn.linear_model import LinearRgression
lr_model = LinearRegression()
lr_model.fit(x,y)  #这里的x和y应当是 形状为n*2的数组类型
a = lr_model.coef_
b = lr_model.intercept_
1
2
3
4
5

预测新数据

predictions = lr_model.predict(x_new) #x_new为一维数组
1

模型评估

均方误差MSE：

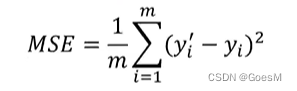
R方值：

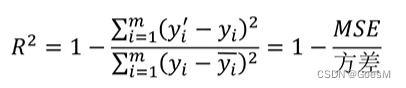
MSE越小越好，R² 越接近1越好

from sklearn.metrics import mean_squared_error, r2_score
MSE = mean_squared_error(y,y_predict)
R2 = r2_score(y,y_predict)
1
2
3

可视化评估

from matplotlib import pyplot as plt
plt.scatter(y,y') # y和y‘差别越小，成图就越接近直线
1
2

多因子拟合 线性回归

拟合

X_multi = data.drop(['y'],axis=1) #除去y轴因子，其他因子均为影响因子
LR_multi = LinearRegression()
LR_multi.fit(X_multi,y) # 求解X_multi与y的关系
1
2
3

预测

y_predict_multi = LR_multi.predict(X_multi_query) # 预测值
1

评估

R方值：

mean_squared_error_multi = mean_squared_error(y,y_predict_multi)
r2_score_multi = r2_score(y,y_predict_multi)
print(r2_score_multi)
1
2
3

可视化（看y和预测y的差值情况）

fig = plt.figure(figsize=(8,5))
plt.scatter(y,y_predict_1)
plt.show()
1
2
3

Part 2. 机器学习之逻辑回归

问题描述

分类问题： 垃圾邮件检测、预测学生是否可以通过考试、图像分类
给定数据集，每个数据都具有多个特征要素，并给定其分类标签。该回归模型就是对 对象特征 进行识别，根据 特征、分类结果

算法逻辑

将“特征描述”进行数字化，转换成数字数据
对曲线进行拟合的方法，除了线性回归以外，还包括且不限于 分段函数、复杂函数等等.

“特征描述”数字化后，得到 特征值–分类标签 的散点图
通过与“线性回归”类似的算法原理，对“分界曲线”进行拟合

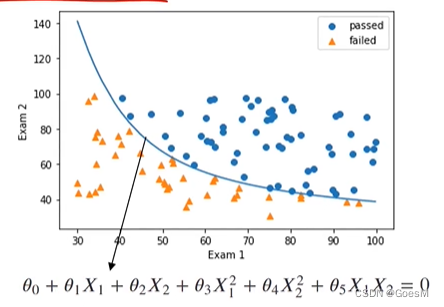
蓝线为拟合出的分界曲线

逻辑回归的损失函数

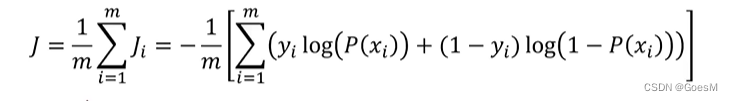
拟合、预测

from sklearn.linear_model import LogisticRegression
lr_model = LogisticRegression()
lr_model.fit(x,y) # 填入散点数据，x为特征值，y为分类标签

#分界函数 （系数计算）
theta1,theta2 = LR.coef_[0][0],LR.coef_[0][1]
theta0 = LR.intercept_[0]

#新数据的类别预测
predictions = lr_model.predict(x_new)
1
2
3
4
5
6
7
8
9
10

评估

准确率： Accuracy = 正确数 / 总数

from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
1
2

Part 3. 机器学习之聚类

KMeans: K均值聚类算法

算法定义：

以空间k个点为中心进行聚类，对最靠近他们的对象归类，是最基础且最重要的聚类算法

算法流程：

step 1. 选择聚类的个数k
step 2. 随机选定这k个聚类中心的位置
step 3. 根据点到聚类中心的距离确定各个点的所属类别
step 4.根据各个类别的数据更新聚类中心（取他们的均值为新的中心）
step 5. 重复step2~step5，直至中心点不再变化

代码实现

聚类拟合

from sklearn.cluster import KMeans
KM = KMeans(n_cluster=3,random_state=0) # n_cluster=想要分为的类别数，random_state初始的随机状态
KM.fit( point ) # point为2D点集数据
centers = KM.cluster_centers_ #获取模型确定的中心点
1
2
3
4

预测

pred_label = KM.predict(  [ [8,6] ]  )
print(pred_label)
1
2

评估-准确率

from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,pred_y)
1
2

类别标签矫正

y_cal = [] #矫正结果数组
for i in pred_y:
	if i == 'lable_name1':
		y_cal.append(2)
	elif i == 1:
		y_cal.append(1)
	else:
		y_cal.append(0)
print(pred_y,y_cal)
1
2
3
4
5
6
7
8
9

KNN算法：K nearest neighbor, K近邻分类模型

算法定义

给定样本数据集，对新的输入实例进行预测
预测方法为：在样本数据集中找到与该实例最邻近的k个样本，这k个样本中出现最多次的类别，就是这个输入实例 的被预测类别

代码实现

拟合

# 拟合
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3) 
# n_neibors = 想要分为3类
KNN.fit(point,label)
1
2
3
4
5

预测

# 预测
pred_label = KNN.predict( [[8,6]] )
print(pred_label)
pred_label = KNN.predict( point )
print(pred_label)
## KNN模型为监督式机器学习，无需另外匹配标签
1
2
3
4
5
6

评估

# 评估
from sklearn.metrics import accuracy_score
print('accuracy：',accuracy_score(label,pred_label))
1
2
3

Mean-shift算法：均值漂移聚类算法

算法定义

一种基于密度梯度上升的聚类算法（沿着密度上升方向寻找聚类中心点）
就是不断地把中心点移动到点聚集的地方，但需要提前预判聚类圆的半径

代码实现

聚类拟合

from sklearn.cluster import MeanShift,estimate_bandwidth
# 估计聚类圆的半径
bandwidth = estimate_bandwidth( X, n_samples=500)
# X 为样本点集数据， n_samples表示样本数量 
1
2
3
4

评估-准确率

from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,pred_y)
1
2

类别标签矫正

y_cal = [] #矫正结果数组
for i in pred_y:
	if i == 'lable_name1':
		y_cal.append(2)
	elif i == 1:
		y_cal.append(1)
	else:
		y_cal.append(0)
print(pred_y,y_cal)
1
2
3
4
5
6
7
8
9

个人想法： 我感觉可以用并查集 写一段自动匹配

Part 4. 机器学习之决策树

Decision Tree
跟深搜一个逻辑，就是多层判断，不断深搜，最终找到答案。
优点：计算量小、易于理解
缺点：忽略了属性之间的相关性：可能有几层判断，其实是相关的；如果样本分布不均匀，会很容易影响模型表现

ID3 决策树算法

算法定义

利用信息熵原理，选择信息增益最大的属性作为分类属性，递归拓展决策树的分支，完成决策树的构造

大白话就是：决策树需要有确定影响决策的“因素”有哪些，这些因素不需要人工输入，可以根据ID3算法直接获取。

代码实现

决策树实现分类

from sklearn import tree
dc_tree = tree.DecisionTreeClassifier(
	criterion='entropy',min_samples_leaf=5)
# 使用'entropy'即ID3信息熵算法，分类标签有5个
#leaf指决策树的每个叶子节点未继续分类的样本数量的最小值，leaf越小越精确度越高
dc_tree.fit( point , label)
1
2
3
4
5
6

可视化决策树

tree.plot_tree(dc_tree,filled='True',feature_names=['表头名1','表头名2','表头名3','表头名4'],class_names=['label1','label2','label3'])
1

其他决策树算法【待填】

C4.5决策树算法【待填】

CART决策树算法【待填】

Part 5. 机器学习之异常检测

Anomaly Detection

概念

对输入的样本数据集，对不符合预期模式的数据进行识别
实现逻辑：计算可得每个位置的概率密度，视概率密度低于一定值的点集为异常点集。
数学原理：任意分布可视为高斯分布，基于高斯分布拟合对样本数据集进行异常检测

代码实现

原始数据分布可视化

plt.hist(x1,bins=100)
#视x1的值为被观测值，划分为100个格子，查看其分布概率图
x1_mean = x1.mean() # u，正态分布的均值
x1_sigma = x1.std() # sigma 正态分布的标准差
print(x1_mean,x1_sigma)
#计算高斯分布数值
from scipy.stats import norm
import numpy as np
x1_range = np.linspace(0,20,300) #x1的范围为(0,20),有300个点
normal1 = norm.pdf(x1_range,x1_mean,x1_sigma) #对range范围内，做分布为N(mean,sigma)的高斯分布, 最终normal1为概率密度函数

plt.plot(x1_range,normal1)
#绘制出拟合的高斯分布曲线
1
2
3
4
5
6
7
8
9
10
11
12
13

模型训练

from sklearn.covariance import EllipticEnvelope
clf = EllipticEnvelope(
    contamination = 0.01 
    #参数contamination表示所给样本数据集的异常概率
)
clf.fit( data ) #data为被检测的数据集合
1
2
3
4
5
6

模型结果

# 异常点显示、异常行为预测
pred_label = clf.predict(data)
print(pred_label)
# 异常点值为-1，正常点值为1
1
2
3
4

异常数据可视化

#在绘制原图代码的后面，加上下列代码
anamoly_points = plt.scatter(
	data.loc[:,'x1'][y_predict==-1], # 选取值为-1的异常数据
	data.loc[:,'x2'][y_predict==-1]. # 选取值为-1的异常数据
	marker='o', #异常数据用O圈起来
	facecolor = 'red',#填充色
	edgecolor = 'red', #边线色
	s=250 #size大小
	)
1
2
3
4
5
6
7
8
9

Part 6. 机器学习之主成分分析

PCA

数据降维

1. 筛除应变量 “不相关”的因变量，筛除“不相关要素”
2. 组合“相关”元素：比如 人口、地理面积的二维数据，可以组合为 人口密度的一维数据
   注：相关不相关的依据是，概率论中的“协方差”概念

PCA算法：principal components analysis

在信息损失尽可能少的情况下，降低数据维度
在n维样本数据集中，寻找k维的新数据，实现n->k的降维。

代码实现

数据预处理
将普通正态分布转换为标准正态分布

from sklearn.preprocessing import StandardScaler
X_norm = StandardScaler().fit_transform(X)
# X为数据的原分布
1
2
3

获取降维数据

from sklearn.decomposition import PCA
pca = PCA(n_components=4) #降维至 4维
X_reduced = pca.fit_transform(X_norm)
1
2
3

观察各个要素的方差比例

var_ratio = pca.explained_variance_ratio_ 
#比例越高，相关性越高
1
2

可视化降维后的数据
借助 matplotlib 绘制 分类散点图即可

Part x. 模型评估与优化

博客跳转：【人工智能】模型评价与优化