2023面试高手

这个屌丝很懒，什么也没留下！

热门标签

【数据结构】带环链表OJ - 细节推理 + 逻辑证明_数据结构中带环相遇问题

作者：2023面试高手 | 2024-02-06 20:47:15

踩

数据结构中带环相遇问题

前言

单链表中同样也有具有挑战性的题目，链表的带环问题可以说是众多难题中的佼佼者，在这里可能更看重的是逻辑推理和证明的过程。

什么是带环链表：

带环链表是链表最后一个结点的指针域不是指向空指针，而是指向链表之前的结点，这样就形成了环状的链表结构。

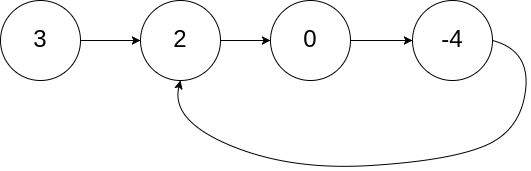
如图所示：

判断链表是否带环：

那么问题来了，如何判断一个链表是否带环呢？

这里我们再次运用了快慢指针，但是快慢指针又该如何具体设置呢？

判断思路：

先定义一个快指针fast，一个慢指针slow。

快指针一定是比慢指针先进环的，当slow进环时，fast指针便开始了追slow指针，当快指针和慢指针相遇的时候，快指针便追上了慢指针，此时就可以判断该链表是有环的，但凡快指针指向空就说明该链表是不带环的。

那么快慢指针一次各走几步最合适呢？

假设slow刚进环时，fast与slow之间的距离为N，环的长度为C。

这里我们要多组讨论一下：（先讨论有代表的两组）

1.slow一次走1步，fast一次走2步一定能追上吗？

2.slow一次走1步，fast一次走3步一定能追上吗？

…………………

图为当slow刚进环时，假设fast所在的位置：

1.slow一次走1步，fast一次走2步一定能追上吗？

每次追击，fast与slow之间的距离就缩小1，当距离N缩小为0的时候，便追上了。

N - 1，N - 2，N - 3，……，0

所以这种情况一定能追上。

2.slow一次走1步，fast一次走3步一定能追上吗？

每次追击，fast与slow之间的距离就缩小2，这里要对N进行讨论：

（1）当N为偶数时，N每次缩小2，当距离N缩小为0的时候，便追上了。

N - 2，N - 4，N - 6，……，0

（2）当N为奇数时，N每次缩小2，当距离N缩小为1的时候，下次追击二者距离扔缩小2，此时 fast就会超过slow，距离N变为 -1 ，也就是C - 1，这时又要对C - 1进行讨论。

当C - 1为偶数时就能追上。
当C - 1为奇数时就扔会错过，N再次变成C - 1，那么就会永远错过也就永远追不上。

所以这种情况不一定能追上，有可能永远追不上。

3.slow一次走1步，fast一次走4步一定能追上吗？

每次追击，fast与slow之间的距离就缩小3，这里又要对N进行讨论：

（1）当N为3的倍数时，N每次缩小3，当距离N缩小为0的时候，便追上了。

N - 3，N - 6，N - 9，……，0

（2）当N不为3的倍数时，那么fast会与slow错过，至于错过时fast超过slow多少距离还需讨论（超过的距离取决于一开始N的长度）。

当追上后，fast超过slow距离为1时，此时fast追slow追击距离为N即（C - 1），此时又要对C - 1进行上述讨论，即C - 1是否为3的倍数的讨论。
当追上后，fast超过slow距离为2时，此时fast追slow追击距离为N即（C - 2），此时又要对C - 2进行上述讨论，即C - 2是否为3的倍数的讨论。

所以这种情况只有当N为3的倍数的时候才能追得上。

综上：能不能追得上取决于两个指针之间的距离N和环的大小C。

下面提供一个结论个人小结：（仅供参考，可能存在局限性）

只要快慢指针的速度差是2的时候，就可能会出现永远追不上的问题。假设fast与slow的速度差为x，那么fast追赶slow一次，他们之间的距离就减少x，途中有可能刚好追上，也有可能错过。当错过的时候，fast在slow前面，这时fast超过slow的距离的取值只可能是在[1 ~ (x - 1)]之间（x取整数）。同时任意一个正整数，假设记作m，（m > x）当m整除一个整数x有余数时，对这个整数m减去[1 ~ (x - 1)]中任意一个值，总能找到一个值x，使得m - x的值能够整除x。所以无论环的长度为多长，假设环的长度为C，总有C减去[1 ~ (x - 1)]中任意一个值，使得C - x能够整除x并且没余数，既然没余数那就是刚好追上的情况。
当fast和slow的速度差为2时，即x = 2的时候，C - x，x属于[1 ~ (x - 1)]，那么C - x就只能是C - 1，那么当C - 1去整除2的时候，如果C - 1为奇数，那么C - 1整除2必然有余数，并且余数为1，下次还是C - 1去整除2，还是会余1，所以这时fast就永远追不上slow。

总结：

设置fast一次走2步，slow一次走1步的时候最保险。因为快慢指针相距N，每追击一次N就减1，总会减到0，N缩小到0就是追到了。

环形链表 I

环形链表

OJ链接

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递。仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。否则，返回 false 。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。


/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head)
{
    struct ListNode* fast, *slow;
    fast = slow = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(slow == fast)
        return true;
    }
 
    return false;
}

思路：

运用上述判断环形链表的结论，fast一次走2步，slow每次走1步，只要是环状就一定会追的到。

找带环形链表入环的第一个结点：

接下来更深层次的问题来了，带环链表环的入口该怎么找呢？

以后带环问题通常都用fast一次走2步，slow一次走1步。

当快指针追到慢指针时，假设相遇点为meet，slow指针和fast指针在如图所示的：

注意：
这里快指针一定是先进环，slow后进环。

slow指针进环后，在走一圈的时间内，一定是会被fast追上的。

思路：

在是slow指针和fast指针，同时从head头开始走，直到在meet点相遇，又因为fast指针的速度为slow指针速度的二倍，那么就一定满足一个等式关系：

快指针走的距离 = 慢指针走的距离 * 2

还需讨论的是当slow进环时，fast在环内走了多久的问题：

当L足够长而C很小时：slow进环时fast可能已经在环内走了好多圈了（假设为n圈）。
当L很小而C足够大时：slow进环时fast可能在环内连一圈还没走。

综合考虑之后再结合上述等式关系变得到下列等式：

L + nC + X = 2 * (L+ X)

化简得：

L = n * C - X

这个公式充分说明了，一个指针从head走，一个指针从相遇点meet走，并且每次都走一步，一直走下去，它们最终会在环的入口点相遇！！！

环形链表 II

环形链表 II

OJ链接

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。不允许修改链表。

示例 1：

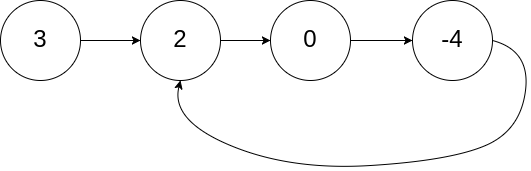
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

思路1：

先运用上述判断环形链表的结论找到相遇点，再运用上述找环形入口点的结论，就能轻松找到环的入口点。


 
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head)
{
    struct ListNode* fast, *slow;
    slow = fast = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(slow == fast)
        {
            struct ListNode* meet = slow;
            while(head != meet)
            {
                meet = meet->next;
                head = head->next;
            }
            return meet;
        }
    }
    return NULL;
}

思路2：

先运用上述判断环形链表的结论找到相遇点，再将相遇点断开，这时就变成了上一篇博客找相交链表公共结点的问题，示意图如下：

参考代码如下：


/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head)
{
    struct ListNode* fast, *slow;
    slow = fast = head;
    int len1 = 0,len2 = 0;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(slow == fast)
        {
            struct ListNode* shortList, *longList, *meet, *longTail, *shortTail;
            longList = longTail = head;
            meet = shortList = shortTail = slow->next;
            slow->next = NULL;
            while(shortTail)
            {
                shortTail = shortTail->next;
                len1++;
            }
            while(longTail)
            {
                longTail = longTail->next;
                len2++;
            }
            int gap = abs(len1 - len2);
            if(len1 > len2)
            {
                longList = meet;
                shortList = head;
            }       
            while(gap--)
            {
                longList = longList->next;
            }     
            while(shortList != longList)
            {
                longList = longList->next;
                shortList = shortList->next;
            }
            return longList;
        }
    }
    return NULL;
}

总结

多总结经验，多做题，规律性的东西也要适当记忆！

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/2023面试高手/article/detail/64506