热门标签
热门文章
- 1高级数据结构 ＜二叉搜索树＞
- 2谁是远程界的天花板？2023年5款最常用的远程软件横测：ToDesk、向日葵、TeamViewer、Splashtop、AnyDesk_远程app有哪些
- 3PoeAI：免费使用GPT-4的AI聊天机器人平台
- 4网络游戏防沉迷实名认证系统常见错误说明_sys req partner error
- 5最火web大屏可视化编辑器_大屏编辑器
- 6人工神经网络的发展历程,神经网络发展历程简述
- 7认识Kubernetes_k8s集群中一个节点是不是一个宿主机
- 8【HarmonyOS】【ArkTS】如何使用HTTP网络请求获取动态数据刷新UI界面_arkts怎么做接口请求
- 9微信小程序项目实例源码——本地电商平台小程序_电商小程序源码
- 10区块链金融科技：技术融合与挑战应对【文末送书-16】
当前位置: article > 正文
Java语言实现的十大排序算法_java语言排序算法
作者：2023面试高手 | 2024-02-07 21:23:43
赞
踩
java语言排序算法
声明：本文来自转载，如有侵权，请联系删除。
原文链接：https://blog.csdn.net/wq_1995/article/details/81937926
目录
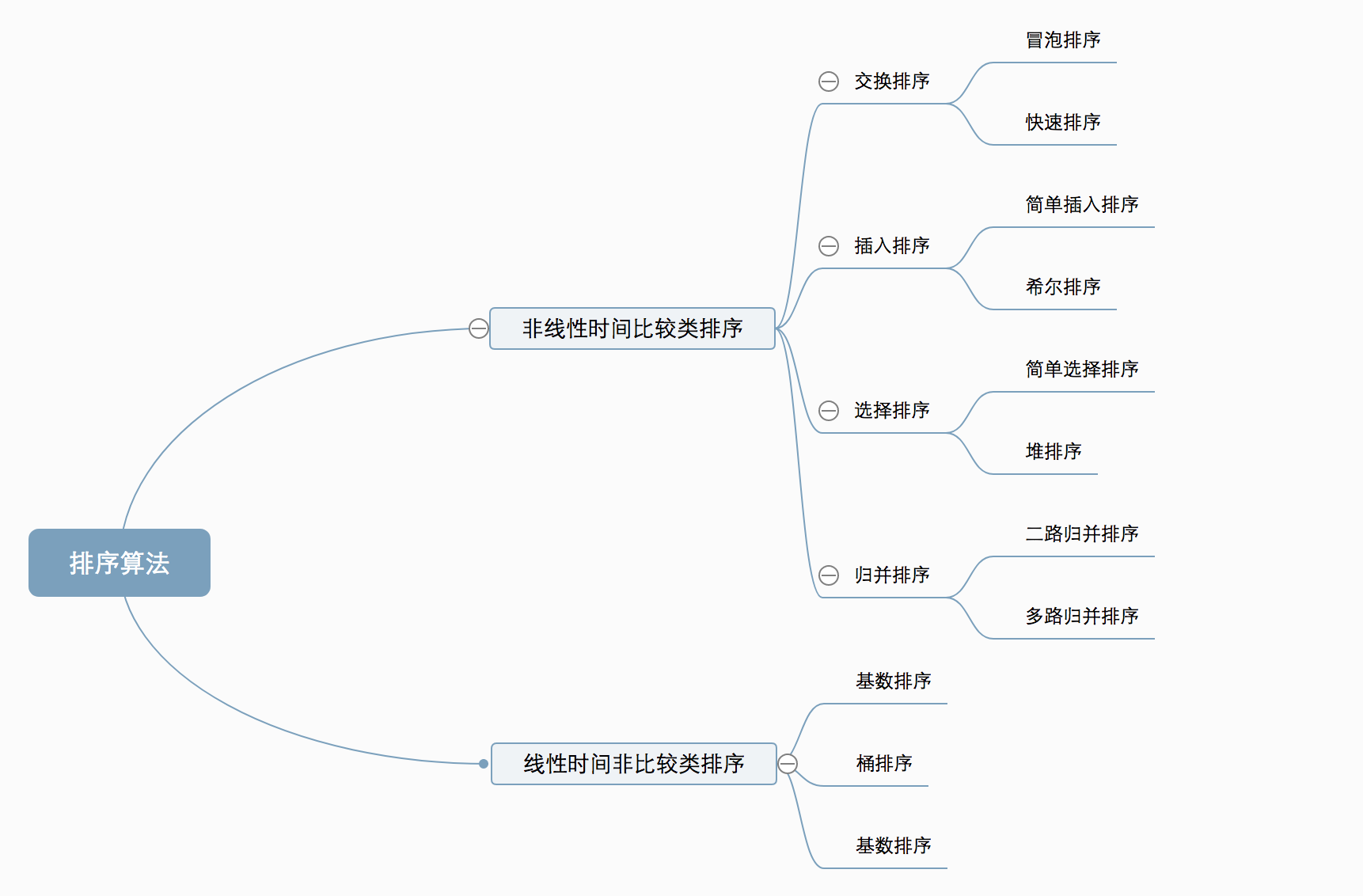
一、算法的分类
1、概念
将杂乱无章的数据元素，通过一定的方法按关键字顺序排列的过程叫做排序。
2、分类
- 非线性时间比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此称为非线性时间比较类排序。
- 线性时间非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此称为线性时间非比较类排序。
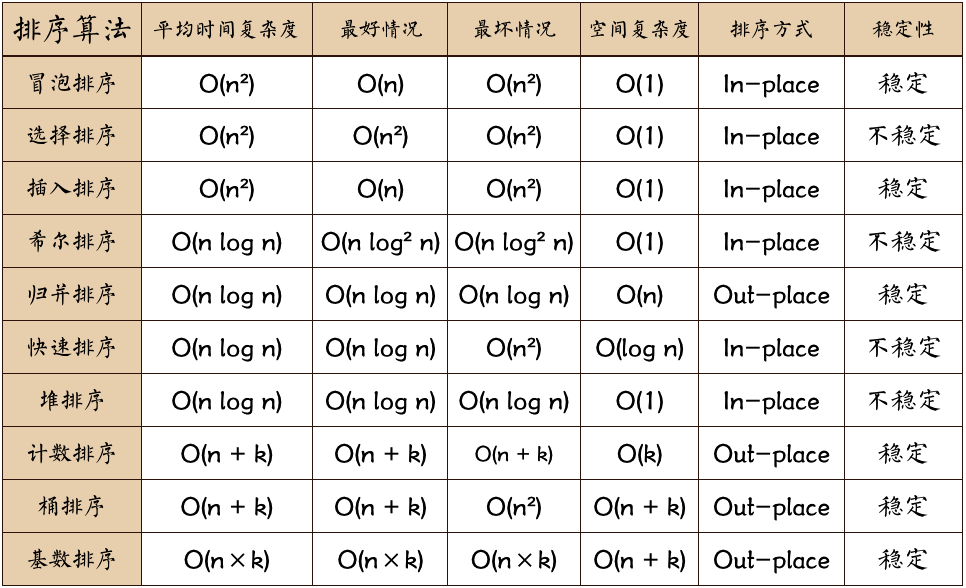
3、比较
说明：
- 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；
- 不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；
- 内排序：所有排序操作都在内存中完成；
- 外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；
二、各算法原理及实现
1、冒泡排序（Bubble Sort）
①、基本思想：两个数比较大小，较大的数下沉，较小的数冒起来。
②、算法描述：
- 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
- 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
- 针对所有的元素重复以上的步骤，除了最后一个；
- 重复步骤1~3，直到排序完成。
③、动图演示：
④、代码实现
-
public
static
int[] bubbleSort(
int[] array) {
-
if (array.length ==
0)
-
return array;
-
for (
int i =
0; i < array.length; i++)
-
for (
int j =
0; j < array.length -
1 - i; j++)
-
if (array[j +
1] < array[j]) {
-
int temp = array[j +
1];
-
array[j +
1] = array[j];
-
array[j] = temp;
-
}
-
return array;
-
}
- 1
2、选择排序（Selection Sort）
①、基本思想：选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
②、算法描述：（n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。）
- 初始状态：无序区为R[1..n]，有序区为空；
- 第i趟排序(i=1,2,3…n-1)开始时，当前有序区和无序区分别为R[1..i-1]和R(i..n）。该趟排序从当前无序区中-选出关键字最小的记录 R[k]，将它与无序区的第1个记录R交换，使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区；
- n-1趟结束，数组有序化了。
③、动图演示
④、代码实现
-
public
static
int[] selectionSort(
int[]
array) {
-
if (
array.length ==
0)
-
return
array;
-
for (
int i =
0; i <
array.length; i++) {
-
int minIndex = i;
-
for (
int j = i; j <
array.length; j++) {
-
if (
array[j] <
array[minIndex])
//找到最小的数
-
minIndex = j;
//将最小数的索引保存
-
}
-
int temp =
array[minIndex];
-
array[minIndex] =
array[i];
-
array[i] = temp;
-
}
-
return
array;
-
}
- 1
3、插入排序（Insertion Sort）
①、基本思想：在要排序的一组数中，假定前n-1个数已经排好序，现在将第n个数插到前面的有序数列中，使得这n个数也是排好顺序的。如此反复循环，直到全部排好顺序。
②、算法描述：
- 从第一个元素开始，该元素可以认为已经被排序；
- 取出下一个元素，在已经排序的元素序列中从后向前扫描；
- 如果该元素（已排序）大于新元素，将该元素移到下一位置；
- 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
- 将新元素插入到该位置后；
- 重复步骤2~5。
③、动图演示
④、代码实现
-
public
static
int[] insertionSort(
int[] array) {
-
if (array.length ==
0)
-
return array;
-
int current;
-
for (
int i =
0; i < array.length -
1; i++) {
-
current = array[i +
1];
-
int preIndex = i;
-
while (preIndex >=
0 && current < array[preIndex]) {
-
array[preIndex +
1] = array[preIndex];
-
preIndex--;
-
}
-
array[preIndex +
1] = current;
-
}
-
return array;
-
}
- 1
4、希尔排序（Shell Sort）
①、基本思想：希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破O(n2）的第一批算法之一。它与插入排序的不同之处在于，它会优先比较距离较远的元素。
②、算法描述：
- 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
- 按增量序列个数k，对序列进行k 趟排序；
- 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。
③、动图演示：
④、代码实现
-
public
static
int[] ShellSort(
int[] array) {
-
int len = array.length;
-
int temp, gap = len /
2;
-
while (gap >
0) {
-
for (
int i = gap; i < len; i++) {
-
temp = array[i];
-
int preIndex = i - gap;
-
while (preIndex >=
0 && array[preIndex] > temp) {
-
array[preIndex + gap] = array[preIndex];
-
preIndex -= gap;
-
}
-
array[preIndex + gap] = temp;
-
}
-
gap /=
2;
-
}
-
return array;
-
}
- 1
⑤、算法分析
希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列，也可以动态的定义间隔序列。
-
while (gap < len /
3) {
// 动态定义间隔序列
-
gap = gap *
3 +
1;
-
}
- 1
5、归并排序（Merge Sort）
①、基本思想：
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。
②、算法描述：
- 把长度为n的输入序列分成两个长度为n/2的子序列；
- 对这两个子序列分别采用归并排序；
- 将两个排序好的子序列合并成一个最终的排序序列。
③、动图演示：
④、代码实现：
-
/**
-
* 归并排序
-
*
-
* @param array
-
* @return
-
*/
-
public
static
int[] MergeSort(
int[] array) {
-
if (array.length <
2)
return array;
-
int mid = array.length /
2;
-
int[] left = Arrays.copyOfRange(array,
0, mid);
-
int[] right = Arrays.copyOfRange(array, mid, array.length);
-
return merge(MergeSort(left), MergeSort(right));
-
}
-
/**
-
* 归并排序——将两段排序好的数组结合成一个排序数组
-
*
-
* @param left
-
* @param right
-
* @return
-
*/
-
public
static
int[] merge(
int[] left,
int[] right) {
-
int[] result =
new
int[left.length + right.length];
-
for (
int index =
0, i =
0, j =
0; index < result.length; index++) {
-
if (i >= left.length)
-
result[index] = right[j++];
-
else
if (j >= right.length)
-
result[index] = left[i++];
-
else
if (left[i] > right[j])
-
result[index] = right[j++];
-
else
-
result[index] = left[i++];
-
}
-
return result;
-
}
- 1
6、快速排序（Quick Sort）
①、基本思想（分治）：
通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。
②、算法描述：快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：
- 从数列中挑出一个元素，称为 “基准”（pivot）；
- 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
- 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。
③、动图演示：
④、代码实现：
-
/**
-
* 快速排序方法
-
* @param array
-
* @param start
-
* @param end
-
* @return
-
*/
-
public
static
int[] QuickSort(
int[] array,
int start,
int end) {
-
if (array.length <
1 || start <
0 || end >= array.length || start > end)
return
null;
-
int smallIndex = partition(array, start, end);
-
if (smallIndex > start)
-
QuickSort(array, start, smallIndex -
1);
-
if (smallIndex < end)
-
QuickSort(array, smallIndex +
1, end);
-
return array;
-
}
-
/**
-
* 快速排序算法——partition
-
* @param array
-
* @param start
-
* @param end
-
* @return
-
*/
-
public static int partition(int[] array, int start, int end) {
-
int pivot = (
int) (start + Math.random() * (end - start +
1));
-
int smallIndex = start -
1;
-
swap(array, pivot, end);
-
for (
int i = start; i <= end; i++)
-
if (array[i] <= array[end]) {
-
smallIndex++;
-
if (i > smallIndex)
-
swap(array, i, smallIndex);
-
}
-
return smallIndex;
-
}
-
-
/**
-
* 交换数组内两个元素
-
* @param array
-
* @param i
-
* @param j
-
*/
-
public static void swap(int[] array, int i, int j) {
-
int temp = array[i];
-
array[i] = array[j];
-
array[j] = temp;
-
}
- 1
7、堆排序（Heap Sort）
①、基本思想：堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。
②、算法描述：
- 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区；
- 将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；
- 由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。
③、动图演示：
④、代码实现：
-
//声明全局变量，用于记录数组array的长度；
-
static
int len;
-
/**
-
* 堆排序算法
-
*
-
* @param array
-
* @return
-
*/
-
public
static
int[] HeapSort(
int[] array) {
-
len = array.length;
-
if (len <
1)
return array;
-
//1.构建一个最大堆
-
buildMaxHeap(array);
-
//2.循环将堆首位（最大值）与末位交换，然后在重新调整最大堆
-
while (len >
0) {
-
swap(array,
0, len -
1);
-
len--;
-
adjustHeap(array,
0);
-
}
-
return array;
-
}
-
/**
-
* 建立最大堆
-
*
-
* @param array
-
*/
-
public static void buildMaxHeap(int[] array) {
-
//从最后一个非叶子节点开始向上构造最大堆
-
for (
int i = (len/
2 -
1); i >=
0; i--) {
//感谢 @让我发会呆 网友的提醒，此处应该为 i = (len/2 - 1)
-
adjustHeap(array, i);
-
}
-
}
-
/**
-
* 调整使之成为最大堆
-
*
-
* @param array
-
* @param i
-
*/
-
public static void adjustHeap(int[] array, int i) {
-
int maxIndex = i;
-
//如果有左子树，且左子树大于父节点，则将最大指针指向左子树
-
if (i *
2 < len && array[i *
2] > array[maxIndex])
-
maxIndex = i *
2;
-
//如果有右子树，且右子树大于父节点，则将最大指针指向右子树
-
if (i *
2 +
1 < len && array[i *
2 +
1] > array[maxIndex])
-
maxIndex = i *
2 +
1;
-
//如果父节点不是最大值，则将父节点与最大值交换，并且递归调整与父节点交换的位置。
-
if (maxIndex != i) {
-
swap(array, maxIndex, i);
-
adjustHeap(array, maxIndex);
-
}
-
}
- 1
8、计数排序（Counting Sort）
①、基本思想：计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。
②、算法描述：
- 找出待排序的数组中最大和最小的元素；
- 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
- 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
- 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。
③、动图演示：
④、代码实现：
-
/**
-
* 计数排序
-
*
-
* @param array
-
* @return
-
*/
-
public
static
int[] CountingSort(
int[] array) {
-
if (array.length ==
0)
return array;
-
int bias, min = array[
0], max = array[
0];
-
for (
int i =
1; i < array.length; i++) {
-
if (array[i] > max)
-
max = array[i];
-
if (array[i] < min)
-
min = array[i];
-
}
-
bias =
0 - min;
-
int[] bucket =
new
int[max - min +
1];
-
Arrays.fill(bucket,
0);
-
for (
int i =
0; i < array.length; i++) {
-
bucket[array[i] + bias]++;
-
}
-
int index =
0, i =
0;
-
while (index < array.length) {
-
if (bucket[i] !=
0) {
-
array[index] = i - bias;
-
bucket[i]--;
-
index++;
-
}
else
-
i++;
-
}
-
return array;
-
}
- 1
9、桶排序（Bucket Sort）
①、基本思想：
桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。
②、算法描述：
- 设置一个定量的数组当作空桶；
- 遍历输入数据，并且把数据一个一个放到对应的桶里去；
- 对每个不是空的桶进行排序；
- 从不是空的桶里把排好序的数据拼接起来。
③、图片演示：
④、代码实现：
-
/**
-
* 桶排序
-
*
-
* @param array
-
* @param bucketSize
-
* @return
-
*/
-
public static ArrayList<Integer> BucketSort(ArrayList<Integer> array, int bucketSize) {
-
if (array ==
null || array.size() <
2)
-
return array;
-
int max = array.get(
0), min = array.get(
0);
-
// 找到最大值最小值
-
for (
int i =
0; i < array.size(); i++) {
-
if (array.get(i) > max)
-
max = array.get(i);
-
if (array.get(i) < min)
-
min = array.get(i);
-
}
-
int bucketCount = (max - min) / bucketSize +
1;
-
ArrayList<ArrayList<Integer>> bucketArr =
new ArrayList<>(bucketCount);
-
ArrayList<Integer> resultArr =
new ArrayList<>();
-
for (
int i =
0; i < bucketCount; i++) {
-
bucketArr.add(
new ArrayList<Integer>());
-
}
-
for (
int i =
0; i < array.size(); i++) {
-
bucketArr.get((array.get(i) - min) / bucketSize).add(array.get(i));
-
}
-
for (
int i =
0; i < bucketCount; i++) {
-
if (bucketSize ==
1) {
// 如果带排序数组中有重复数字时 感谢 @见风任然是风 朋友指出错误
-
for (
int j =
0; j < bucketArr.get(i).size(); j++)
-
resultArr.add(bucketArr.get(i).get(j));
-
}
else {
-
if (bucketCount ==
1)
-
bucketSize--;
-
ArrayList<Integer> temp = BucketSort(bucketArr.get(i), bucketSize);
-
for (
int j =
0; j < temp.size(); j++)
-
resultArr.add(temp.get(j));
-
}
-
}
-
return resultArr;
-
}
- 1
10、基数排序（Radix Sort）
①、基本思想：
基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。
②、算法描述：
- 取得数组中的最大数，并取得位数；
- arr为原始数组，从最低位开始取每个位组成radix数组；
- 对radix进行计数排序（利用计数排序适用于小范围数的特点）；
③、动图演示：
④、代码实现：
-
/**
-
* 基数排序
-
* @param array
-
* @return
-
*/
-
public
static
int[] RadixSort(
int[] array) {
-
if (array ==
null || array.length <
2)
-
return array;
-
// 1.先算出最大数的位数；
-
int max = array[
0];
-
for (
int i =
1; i < array.length; i++) {
-
max = Math.max(max, array[i]);
-
}
-
int maxDigit =
0;
-
while (max !=
0) {
-
max /=
10;
-
maxDigit++;
-
}
-
int mod =
10, div =
1;
-
ArrayList<ArrayList<Integer>> bucketList =
new ArrayList<ArrayList<Integer>>();
-
for (
int i =
0; i <
10; i++)
-
bucketList.add(
new ArrayList<Integer>());
-
for (
int i =
0; i < maxDigit; i++, mod *=
10, div *=
10) {
-
for (
int j =
0; j < array.length; j++) {
-
int num = (array[j] % mod) / div;
-
bucketList.get(num).add(array[j]);
-
}
-
int index =
0;
-
for (
int j =
0; j < bucketList.size(); j++) {
-
for (
int k =
0; k < bucketList.get(j).size(); k++)
-
array[index++] = bucketList.get(j).get(k);
-
bucketList.get(j).clear();
-
}
-
}
-
return array;
-
}
- 1
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/2023面试高手/article/detail/67431
推荐阅读
相关标签
