常见的7种排序算法

1、冒泡排序

最简单的一种排序算法。假设长度为n的数组arr，要按照从小到大排序。则冒泡排序的具体过程可以描述为：首先从数组的第一个元素开始到数组最后一个元素为止，对数组中相邻的两个元素进行比较，如果位于数组左端的元素大于数组右端的元素，则交换这两个元素在数组中的位置。这样操作后数组最右端的元素即为该数组中所有元素的最大值。接着对该数组除最右端的n-1个元素进行同样的操作，再接着对剩下的n-2个元素做同样的操作，直到整个数组有序排列。算法的时间复杂度为O(n^2)。

/* 冒泡排序 */
void BubbleSort(int arr[], int length)
{
	for (int i = 0; i < length; i++)
	{
		for (int j = 0; j < length -  i - 1; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				int temp;
				temp = arr[j + 1];
				arr[j + 1] = arr[j];
				arr[j] = temp;
			}
		}
	}
}

2、选择排序

严蔚敏版《数据结构》中对选择排序的基本思想描述为：每一趟在n-i+1(i=1,2,...,n-1)个记录中选取关键字最小的记录作为有序序列中第i个记录。具体来说，假设长度为n的数组arr，要按照从小到大排序，那么先从n个数字中找到最小值min1，如果最小值min1的位置不在数组的最左端(也就是min1不等于arr[0])，则将最小值min1和arr[0]交换，接着在剩下的n-1个数字中找到最小值min2，如果最小值min2不等于arr[1]，则交换这两个数字，依次类推，直到数组arr有序排列。算法的时间复杂度为O(n^2)。

/* 选择排序 */
void SelectionSort(int arr[], int length)
{
    int index, temp;
 
	for (int i = 0; i < length; i++)
	{
        index = i;
		for (int j = i + 1; j < length; j++)
		{
			if (arr[j] < arr[index])
				index = j;
		}
		if (index != i)
		{
			temp = arr[i];
			arr[i] = arr[index];
			arr[index] = temp;
		}
	}
}

3、插入排序

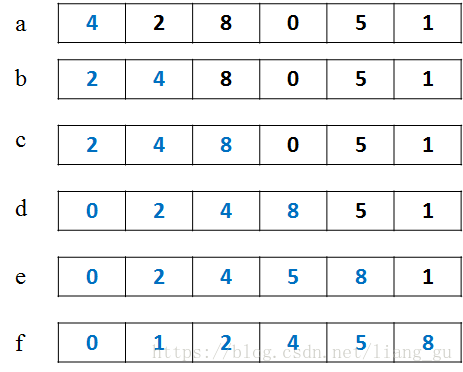
 插入排序的基本思想就是将无序序列插入到有序序列中。例如要将数组arr=[4,2,8,0,5,1]排序，可以将4看做是一个有序序列(图中用蓝色标出)，将[2,8,0,5,1]看做一个无序序列。无序序列中2比4小，于是将2插入到4的左边，此时有序序列变成了[2,4]，无序序列变成了[8,0,5,1]。无序序列中8比4大，于是将8插入到4的右边，有序序列变成了[2,4,8],无序序列变成了[0,5,1]。以此类推，最终数组按照从小到大排序。该算法的时间复杂度为O(n^2)。

// 插入排序
void InsertSort(int arr[], int length)
{
	for (int i = 1; i < length; i++)
	{
		int j;
		if (arr[i] < arr[i - 1])
		{
			int temp = arr[i];
			for (j = i - 1; j >= 0 && temp < arr[j]; j--)
			{
				arr[j + 1] = arr[j];
			}
			arr[j + 1] = temp;
		}
	}
}

4、希尔排序

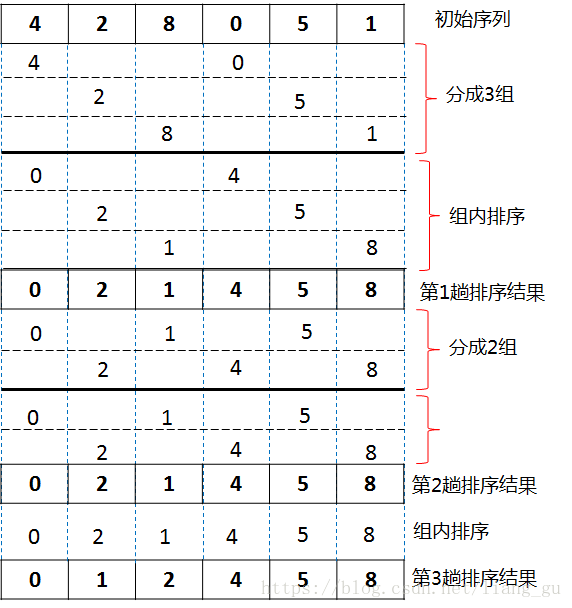
希尔排序(Shell's Sort)在插入排序算法的基础上进行了改进，算法的时间复杂度与前面几种算法相比有较大的改进。其算法的基本思想是：先将待排记录序列分割成为若干子序列分别进行插入排序，待整个序列中的记录"基本有序"时，再对全体记录进行一次直接插入排序。

// 插入排序
void ShellSort(int arr[], int length)
{
	int increasement = length;
	int i, j, k;
	do
	{
		// 确定分组的增量
		increasement = increasement / 3 + 1;
		for (i = 0; i < increasement; i++)
		{
			for (j = i + increasement; j < length; j += increasement)
			{
				if (arr[j] < arr[j - increasement])
				{
					int temp = arr[j];
					for (k = j - increasement; k >= 0 && temp < arr[k]; k -= increasement)
					{
						arr[k + increasement] = arr[k];
					}
					arr[k + increasement] = temp;
				}
			}
		}
	} while (increasement > 1);
}

  5、快速排序

快速排序的基本思想是：通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，已达到整个序列有序。一趟快速排序的具体过程可描述为：从待排序列中任意选取一个记录(通常选取第一个记录)作为基准值，然后将记录中关键字比它小的记录都安置在它的位置之前，将记录中关键字比它大的记录都安置在它的位置之后。这样，以该基准值为分界线，将待排序列分成的两个子序列。

一趟快速排序的具体做法为：设置两个指针low和high分别指向待排序列的开始和结尾，记录下基准值baseval(待排序列的第一个记录)，然后先从high所指的位置向前搜索直到找到一个小于baseval的记录并互相交换，接着从low所指向的位置向后搜索直到找到一个大于baseval的记录并互相交换，重复这两个步骤直到low=high为止。

// 快速排序
void QuickSort(int arr[], int start, int end)
{
	if (start >= end)
		return;
	int i = start;
	int j = end;
	// 基准数
	int baseval = arr[start];
	while (i < j)
	{
		// 从右向左找比基准数小的数
		while (i < j && arr[j] >= baseval)
		{
			j--;
		}
		if (i < j)
		{
			arr[i] = arr[j];
			i++;
		}
		// 从左向右找比基准数大的数
		while (i < j && arr[i] < baseval)
		{
			i++;
		}
		if (i < j)
		{
			arr[j] = arr[i];
			j--;
		}
	}
	// 把基准数放到i的位置
	arr[i] = baseval;
	// 递归
	QuickSort(arr, start, i - 1);
	QuickSort(arr, i + 1, end);
}

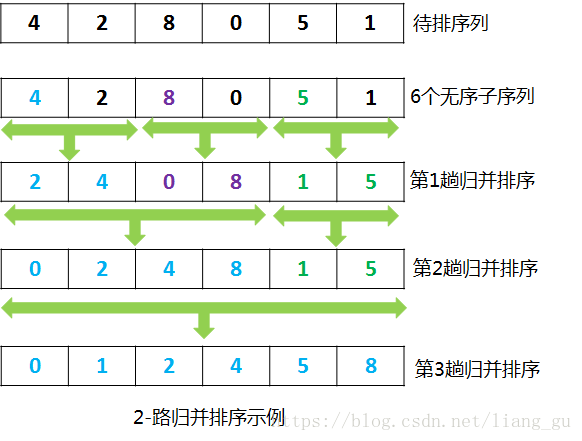
6、归并排序

“归并”的含义是将两个或两个以上的有序序列组合成一个新的有序表。假设初始序列含有n个记录，则可以看成是n个有序的子序列，每个子序列的长度为1，然后两两归并，得到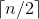（表示不小于x的最小整数）个长度为2(或者是1)的有序子序列，再两两归并。如此重复，直到得到一个长度为n的有序序列为止。这种排序方法称为2-路归并排序。

// 归并排序
void MergeSort(int arr[], int start, int end, int * temp)
{
	if (start >= end)
		return;
	int mid = (start + end) / 2;
	MergeSort(arr, start, mid, temp);
	MergeSort(arr, mid + 1, end, temp);
 
	// 合并两个有序序列
	int length = 0; // 表示辅助空间有多少个元素
	int i_start = start;
	int i_end = mid;
	int j_start = mid + 1;
	int j_end = end;
	while (i_start <= i_end && j_start <= j_end)
	{
		if (arr[i_start] < arr[j_start])
		{
			temp[length] = arr[i_start]; 
			length++;
			i_start++;
		}
		else
		{
			temp[length] = arr[j_start];
			length++;
			j_start++;
		}
	}
	while (i_start <= i_end)
	{
		temp[length] = arr[i_start];
		i_start++;
		length++;
	}
	while (j_start <= j_end)
	{
		temp[length] = arr[j_start];
		length++;
		j_start++;
	}
	// 把辅助空间的数据放到原空间
	for (int i = 0; i < length; i++)
	{
		arr[start + i] = temp[i];
	}
}

7、堆排序

堆的定义如下: n个元素的序列{k1, k2, ... , kn}当且仅当满足一下条件时，称之为堆。

                

可以将堆看做是一个完全二叉树。并且，每个结点的值都大于等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于等于其左右孩子结点的值，称为小顶堆。

堆排序(Heap Sort)是利用堆进行排序的方法。其基本思想为：将待排序列构造成一个大顶堆(或小顶堆)，整个序列的最大值(或最小值)就是堆顶的根结点，将根节点的值和堆数组的末尾元素交换，此时末尾元素就是最大值(或最小值)，然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中的次大值(或次小值)，如此反复执行，最终得到一个有序序列。

/*
	@param arr 待调整的数组
	@param i 待调整的结点的下标
	@param length 数组的长度
*/
void HeapAdjust(int arr[], int i, int length)
{
	// 调整i位置的结点
	// 先保存当前结点的下标
	int max = i;
	// 当前结点左右孩子结点的下标
	int lchild = i * 2 + 1;
	int rchild = i * 2 + 2;
	if (lchild < length && arr[lchild] > arr[max])
	{
		max = lchild;
	}
	if (rchild < length && arr[rchild] > arr[max])
	{
		max = rchild;
	}
	// 若i处的值比其左右孩子结点的值小，就将其和最大值进行交换
	if (max != i)
	{
		int temp;
		temp = arr[i];
		arr[i] = arr[max];
		arr[max] = temp;
		// 递归
		HeapAdjust(arr, max, length);
	}
}
 
// 堆排序
void HeapSort(int arr[], int length)
{
	// 初始化堆
	// length / 2 - 1是二叉树中最后一个非叶子结点的序号
	for (int i = length / 2 - 1; i >= 0; i--)
	{
		HeapAdjust(arr, i, length);
	}
	// 交换堆顶元素和最后一个元素
	for (int i = length - 1; i >= 0; i--)
	{
		int temp;
		temp = arr[i];
		arr[i] = arr[0];
		arr[0] = temp;
		HeapAdjust(arr, 0, i);
	}
}