- 1SSH隧道详解与使用AutoSSH实现稳定的内网穿透_ssh隧道会影响性能吗
- 2Android 稳定性(二) ANR和容灾知识点记录_signal_quit
- 3【Apollo】阿波罗自动驾驶:塑造自动驾驶技术的未来
- 4svn的备份_svn备份操作
- 5干货满满!亲测国内四大AI智能抠图网站_开通ai智能抠图一年多少钱
- 6Java架构师之路三、网络通信:TCP/IP协议、HTTP协议、RESTful API、WebSocket、RPC等。_熟悉http协议、web架构、 restfuiapi及互联网应用的工作原
- 7NXP实战笔记(七):S32K3xx基于RTD-SDK在S32DS上配置ICU输入捕获
- 8C#中使用DevExpress的Ribbton控件中有关Mac office的风格没有系统自带File菜单问题处理_devexpress有没有mac风格的窗口
- 9基于Python+Flask+Echart实现二手车数据分析展示_flask二手车
- 10Python实现图像识别(使用CNN算法)_python图像识别的cnn编程
对数螺旋线(等角螺旋线)数学公式推导
赞
踩
在某些论文或文章里看到对数(等角)螺旋线的公式: 。但是搜索了一下,通常都是一些讲解对数等角螺旋线的性质的结果以及公式结果,并没有详细的公式推导。当然对于大多数人只要知道上述公式就好了,当作一个结论公式使用。
。但是搜索了一下,通常都是一些讲解对数等角螺旋线的性质的结果以及公式结果,并没有详细的公式推导。当然对于大多数人只要知道上述公式就好了,当作一个结论公式使用。
当然也有像我这样的想知道公式怎么推出了的,因此我写下这篇文章,希望能够帮助到大家。因本人才疏学浅,文章定有不足,希望大家能够在评论区讨论以及指正。
废话不多说,开启正文!
一、图形引入
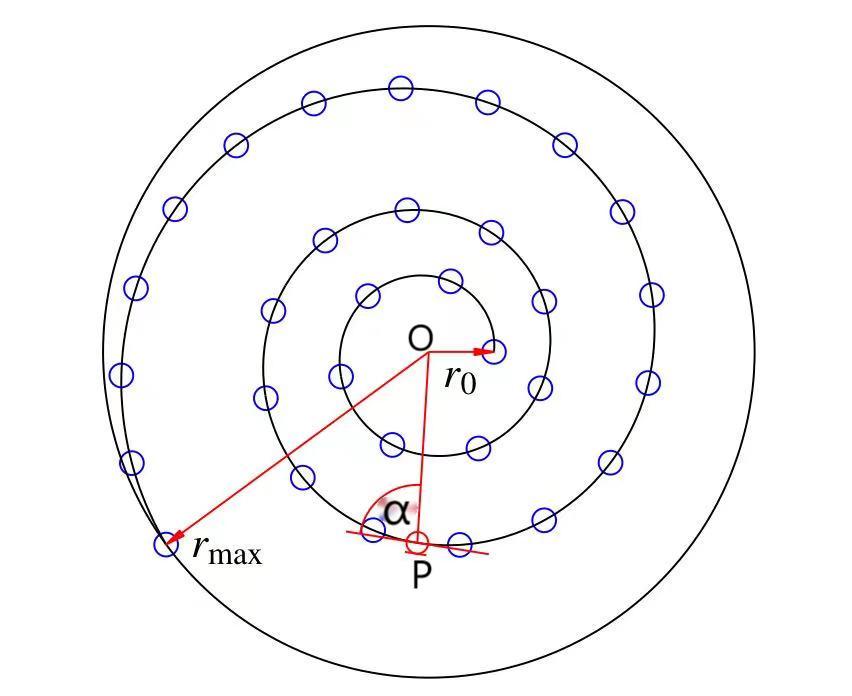
下面是对数(等角)螺旋线的图片,可以清晰看出它的性质:图中曲线的在一任意点P处的切线与圆心O到这一点的连线所成角度α不变,也就是α是一个定值。
二、数学公式推导
若在极坐标系中,对数(等角)螺旋线的极坐标方程为:
 ,其中θ表示任意一点P的角度,因此该点极坐标为
,其中θ表示任意一点P的角度,因此该点极坐标为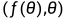 。由推导可知该点的切向量为
。由推导可知该点的切向量为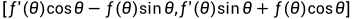
切向量推导过程如下:
点P的极坐标为
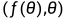 ,因此在直角坐标系中的坐标为
,因此在直角坐标系中的坐标为
再分别对x,y轴坐标进行求导,
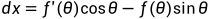 ,
,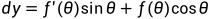
因此可得该点的切向量为:
因为α为该点的切向量与圆心连线的夹角,并且α是一个定值,这个角的大小永远不变,那么接下来就是要求出
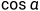 这个定值,推导过程如下:
这个定值,推导过程如下:
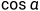 求解过程如下:
求解过程如下:
已知两向量的夹角公式为:
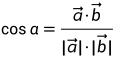 ,
,
所以
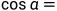
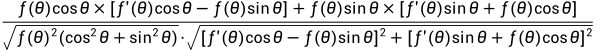
对上式化简:
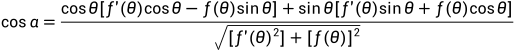
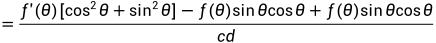
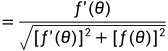
得到
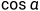 的值后,继续求得
的值后,继续求得 的值:
的值:
 求解过程如下:
求解过程如下:
已知
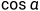 可求得
可求得 ,因为
,因为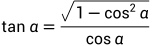
所以,
已知
 可得
可得 ,因为
,因为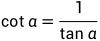
所以,
继续求得最终对数(等角)螺旋线的极坐标方程:
极坐标方程推导如下:
已知

对上述式子两端积分可得,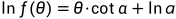 ,其中
,其中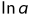 为常数
为常数
化简上式,得到
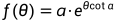
所以,对数(等角)螺旋线的极坐标方程为:
 ,a为常数
,a为常数
三、性质
以上便是对数(等角)螺旋线极坐标方程的推导,根据公式: ,可以得到一些性质。
,可以得到一些性质。
对于每一个θ,都有一个r值相对应;当θ=0时,r=a,因此a可以影响螺旋线距离圆心的距离。其他的性质就不说那么多了,百度上很多讲性质的。
总结:打公式不易,如有错误欢迎指正!麻烦点赞收藏给个鼓励,谢谢~
最后再补充一张MATLAB实现的图吧!