数据结构----完全二叉树的时间复杂度讲解,堆排序_java 完全二叉树时间复杂度

目录

一.建堆的时间复杂度

1.向上调整算法建堆

2.向下调整算法建堆

二.堆排序

1.概念

2.代码思路

3.代码实现

---

一.建堆的时间复杂度

1.向上调整算法建堆

我们就以极端情况考虑时间复杂度(满二叉树+遍历所有层)

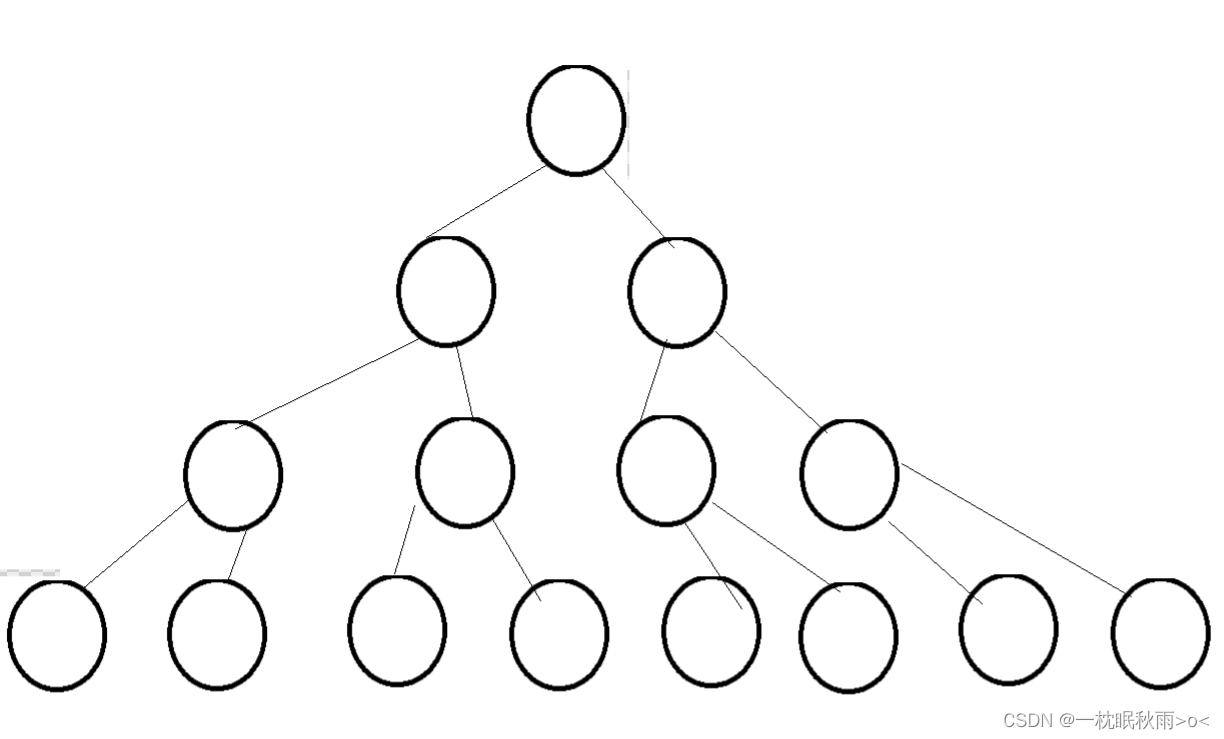
假设所有节点个数为N,树的高度为h

N = 2^0+2^1+2^2......+2^(h-1)

即N = 2^h - 1

h = log(N+1)

时间复杂度我们以交换次数为标准

1        0

2        2^0*2^1

3        2^1*2^2

...

h       2^(h-2)*2^(h-1)

F(h) = 2^0*2^1+2^1*2^2+...+2^(h-2)*2^(h-1)

       = 2^h*(h-2)+2

F(N) = (N+1)(log(N+1)-2)+2(这是详细的时间复杂度函数,粗略记为O(N*logN))

2.向下调整算法建堆

1        (h-1)

2        2^1*(h-2)

3        2^2*(h-3)

...

h-1    2^(h-2)*1

h       2^(h-1)*0

找到倒数第一个非叶节点开始向下调整

F(h) = 2^h-1-(h-1)

F(N) = N-log(N+1)(粗略记为O(N))

二.堆排序

1.概念

堆排序（Heap Sort）是一种高效的排序算法，它利用了“二叉堆”这种数据结构来进行排序。
 
堆是一种特殊的树状结构，分为最大堆和最小堆。在最大堆中，每个父节点的值都大于或等于其子节点的值；而在最小堆中，每个父节点的值都小于或等于其子节点的值。
 
堆排序的基本思想是：将待排序的序列构建成一个最大堆，然后将最大值（即堆的根节点）与序列的最后一个元素交换位置，并将剩余元素重新构建为一个最大堆。重复这个过程，直到整个序列有序。
 
堆排序的时间复杂度为 O(n \log n)，空间复杂度为 O(1)。它是一种不稳定的排序算法，适用于排序整数、浮点数或其他可比较的数据类型。
 
堆排序的优点包括：
 
1. 时间复杂度较低：堆排序的时间复杂度为 O(n \log n)，在平均情况下比其他一些排序算法（如冒泡排序、插入排序）快得多。
2. 空间复杂度低：堆排序的空间复杂度为 O(1)，它不需要额外的存储空间来保存排序后的结果，只使用了固定的辅助空间。
3. 适用于大型数据集：堆排序可以有效地处理大型数据集，因为它的时间复杂度和空间复杂度都比较低。
 
堆排序的缺点包括：
 
1. 不稳定：堆排序是一种不稳定的排序算法，这意味着在排序过程中可能会改变相同值元素的相对顺序。
2. 难以理解和实现：堆排序的概念和操作相对复杂，对于初学者来说可能比较难以理解和实现。
 
总的来说，堆排序是一种高效的排序算法，但在选择排序算法时需要根据具体情况考虑其优缺点。如果对排序的稳定性要求较高，则可能需要选择其他排序算法。

堆排序的平均性能为O(nlogn)。它的时间复杂度和空间复杂度都比较低，适用于排序整数、浮点数或其他可比较的数据类型。
 
在最坏情况下，堆排序的时间复杂度为O(nlog2n)。因此，堆排序的平均性能较接近于最坏性能。

2.代码思路

这里我们采用向下调整法

比如这里有一个大堆,要把它排成升序数组

 7 4 5 1 4 3

                s

首尾交换,把大数据放后面

 3 4 5 1 4 7

             s

让后向下调整,把下一个大数据调到堆顶

5 4 3 1 4 7

             s

首尾交换,把大数据放后面

4 4 3 1 5 7

         s

1 4 3 4 5 7

      s

4 1 3 4 5 7

      s

3 1 4 4 5 7

   s

1 3 4 4 5 7

s

3.代码实现

void adjustDown(HeapDataType* p, int size, int parent)
{
	int child = parent * 2 + 1;
	if (p[child] < p[child + 1])
		child++;
	while (child <= size)
	{
		if (child + 1 <= size && p[parent] < p[child])
		{
			Swap(&p[parent], &p[child]);
			parent = child;
			child = child * 2 + 1;
			if (p[child] < p[child + 1])
				child++;
		}
		else break;
	}
}
void heapSort(HeapDataType* p, int size)
{
	//建堆,一般采用向下调整法
	//向下调整法建堆的时间复杂度为O(N)
	//向上调整法时间复杂度为O(N*logN)
	for (int i = (size - 1 - 1) / 2; i >= 0; i--)
		adjustDown(p, size, i);
	//堆排序,升序用大堆,降序用小堆
	while (size > 0)
	{
		Swap(&p[0], &p[size - 1]);
		size--;
		adjustDown(p, size, 0);
	}
}