2019年五一杯数学建模B题木板最优切割方案解题全过程文档及程序_2019五一竞赛建模b题

2019年五一杯数学建模

B题 木板最优切割方案

原题再现

  徐州某家具厂新进一批木板如表 1 所示，在家具加工的过程中，需要使用切割工具生产表 2所示的产品。假设：木板厚度和割缝宽度忽略不计。

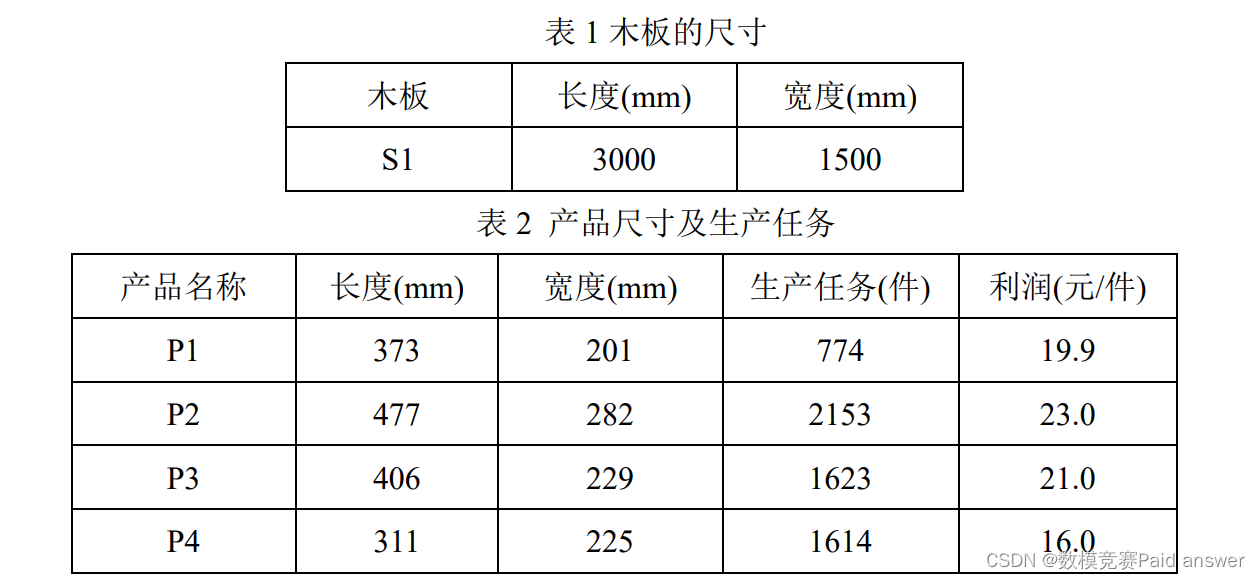
  请为该家具厂给出如下问题的木板最优切割方案。
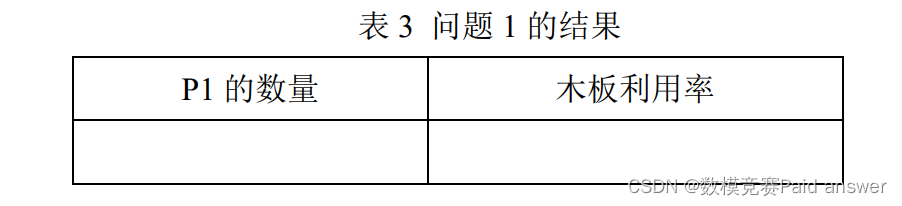
  1. 在一块木板上切割 P1 产品，建立数学模型，给出木板利用率最高(即剩余木板面积最小)的切割方案，并将最优方案的结果填入表 3。

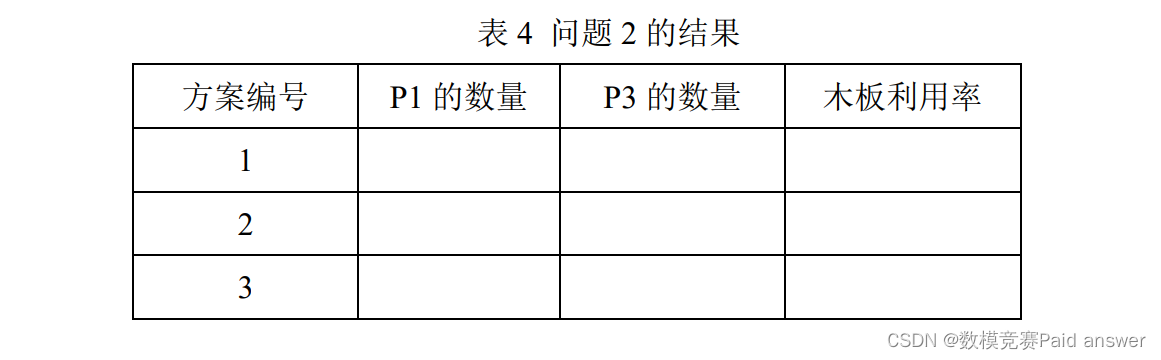
  2. 在一块木板上切割 P1 和 P3 产品，建立数学模型，给出按照木板利用率由高到低排序的前 3 种切割方案，并将结果填入表 4。

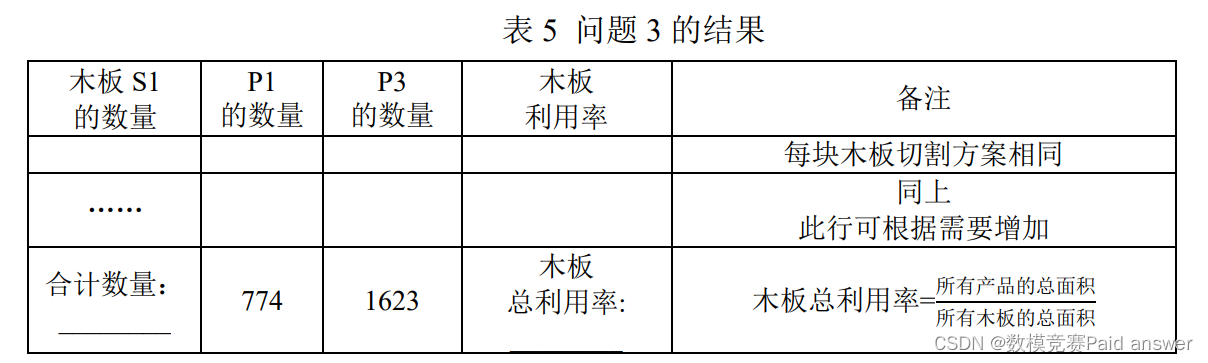
  3. 需要完成表 2 中 P1 和 P3 产品的生产任务，建立数学模型，给出木板总利用率最高的切割方案，并将结果填入表 5。

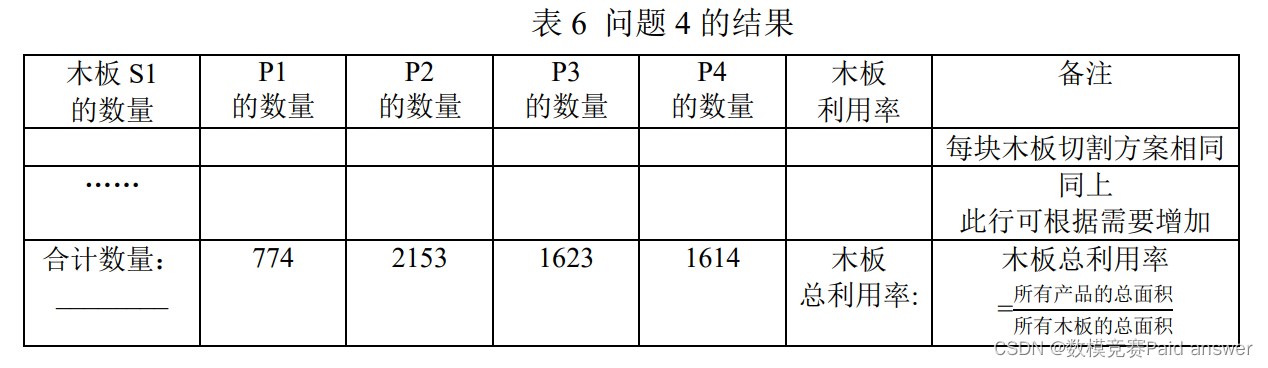
  4. 需要完成表 2 中 P1、P2、P3、P4 产品的生产任务，建立数学模型，给出木板总利用率最高的切割方案，并将结果填入表 6。

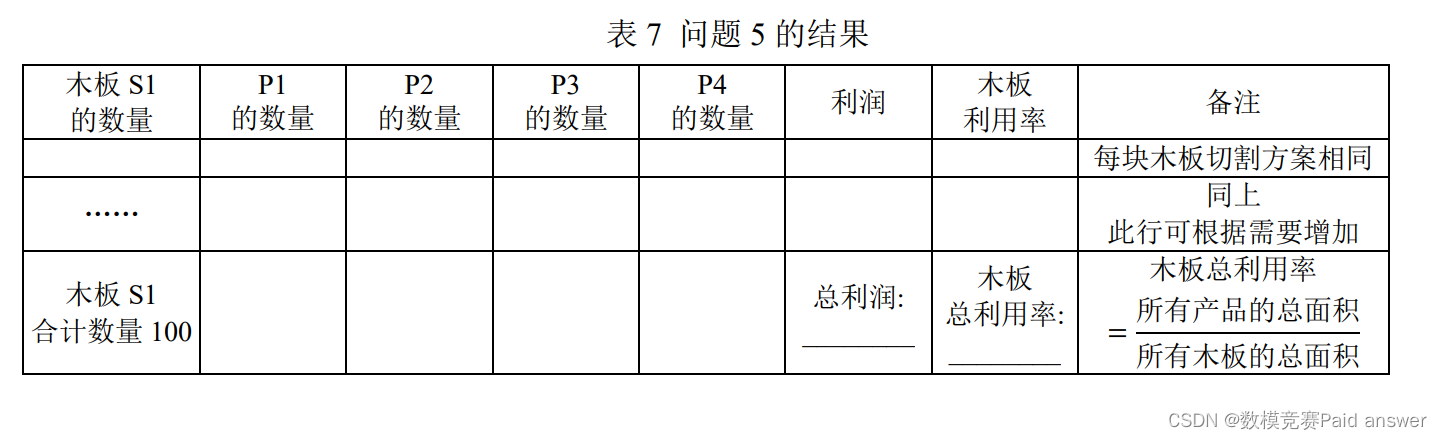
  5. 不考虑产品P1，P2，P3，P4的需求数量，给定100张S1木板，按照表2中给出的利润，建立数学模型，给出总利润最大的切割方案，并将结果填入表7。

整体求解过程概述(摘要)

  本文主要研究了在给定条件下如何对木板最优切割问题，重点研究分析了不同情况下的切割方案，通过建立线性规划模型和混合整数规划模型，并利用 MATLAB和 LINGO 对提出的模型进行求解，具体结果如下：
  对于问题一：考虑到只切割 P1 产品，若想木板利用率最高，只需切割产品的总面积最大，根据两个产品不能重叠，引入了坐标的思想，建立线性规划模型，结合 MATLAB 里的 fmincon 函数求解，得出：在只切割 P1 产品时，一块木板上能够切割 59 块 P1 产品，最高木板利用率为 98.30%。
  对于问题二：在问题一模型的基础上，添加变量