【数据结构与算法】前缀和+哈希表算法_hashtable first second

一、引入

关于前缀和和哈希这两个概念大家都不陌生，在之前的文章中也有过介绍：前缀和与差分算法详解

而哈希表最经典的一题莫过于两数之和
题目链接

题目描述：

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

只会存在一个有效答案

思路分析：
我们在遍历这个数组要做两件事：
假设现在遍历到下标为idx的位置。
1️⃣ 查看target - nums[idx]是否在哈希表中，如果在，说明这两个数加起来就是目标和，那么就找到了两个下标，一个是hash[target - nums[idx]]，一个是当前位置idx。
2️⃣ 用哈希表记录两个数据，first记录当前位置的值，second记录当前位置的下标。

代码：

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> hash;
        int n = nums.size();
        for(int i = 0; i < n; i++)
        {
            if(hash.find(target - nums[i]) != hash.end())
            {
                return {hash[target - nums[i]], i};
            }
            hash[nums[i]] = i;
        }
        return {};
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

二、前缀和与哈希表的结合

用一个例子来说明以下：

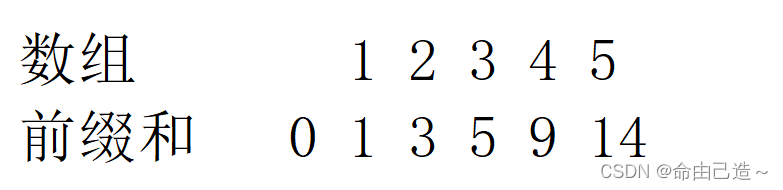
假设我们要寻和为5的连续子数组的个数，那么只要前缀和中任意两个数的差值为5，那么就找到了子数组。

那么我们就可以直接用哈希表把前缀和的数据存储起来，first存前缀和的值，second用来标识有多少个子数组。
这里首先要注意初始化哈希表把0的位置先设置成1：hash[0] = 1，因为当我们计算前缀和为5的位置的时候，就标识了从0 ~ 5存在和为5的连续子数组。

假设目标和为k，遍历到i位置。
所以现在我们在计算前缀和的同时看看是否存在hash[k - nums[i]]，这个的数值大小就代表有多少个连续的子数组和。那么为什么会存在多个呢？

因为可能数组存在负数，这样就会导致出现这种情况：

那么省略号这段区间的前缀总和就为0，所以就会存在两段子数组和为5的区间。

三、例题

3.1 和为 K 的子数组

题目链接

题目描述：

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的连续子数组的个数 。

示例 1：

输入：nums = [1,1,1], k = 2
输出：2

示例 2：

输入：nums = [1,2,3], k = 3
输出：2

思路分析：
这个题如果我们只使用前缀和：先计算前缀和，然后依次遍历看是否有两个数字的差值为k。

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int n = nums.size();
        // 前缀和数组
        vector<int> sums(n + 1);
        for(int i = 0; i < n; i++)
        {
            sums[i + 1] = sums[i] + nums[i];
        }
        int res = 0;
        for(int i = 0; i < n; i++)
        {
            for(int j = i; j < n; j++)
            {
                if(sums[j + 1] - sums[i] == k)
                {
                    res++;
                }
            }
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

但是提交会发现运行超时。
而由于这道题只关心次数，不关注具体的解，所以我们能用哈希表来优化效率。
具体的做法在上面已经详细介绍过。

代码：

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int n = nums.size();
        unordered_map<int, int> hash;
        int res = 0;
        hash[0] = 1;
        int sum = 0;
        for(int i = 0; i < n; i++)
        {
            sum += nums[i];
            res += hash[sum - k];
            hash[sum]++;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

3.2 统计「优美子数组」

题目链接

题目描述：

给你一个整数数组 nums 和一个整数 k。如果某个连续子数组中恰好有 k 个奇数数字，我们就认为这个子数组是「优美子数组」。
请返回这个数组中 「优美子数组」 的数目。

示例 1：

输入：nums = [1,1,2,1,1], k = 3
输出：2
解释：包含 3 个奇数的子数组是 [1,1,2,1] 和 [1,2,1,1] 。

示例 2：

输入：nums = [2,4,6], k = 1
输出：0
解释：数列中不包含任何奇数，所以不存在优美子数组。

示例 3：

输入：nums = [2,2,2,1,2,2,1,2,2,2], k = 2
输出：16

思路分析：
这道题乍一看无从下手，但其实这道题跟上面一道题没什么区别，只要把偶数看成0，奇数看成1，就直接转化成了和为K的子数组问题了。

代码：

class Solution {
public:
    int numberOfSubarrays(vector<int>& nums, int k) {
        int n = nums.size();
        int res = 0;
        unordered_map<int, int> hash;
        hash[0] = 1;
        int sum = 0;
        for(int i = 0; i < n; i++)
        {
            // 偶数为0,奇数为1
            int ret = 0;
            if(nums[i] % 2)
            {
                ret = 1;
            }
            sum += ret;
            res += hash[sum - k];
            hash[sum]++;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

3.3 路径总和III

题目链接

题目描述：

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

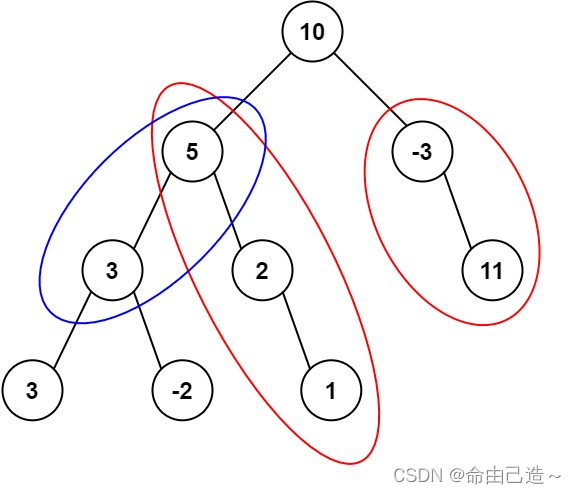
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

方法一：
这道题可以直接用暴力遍历，每个节点都往下统计到叶子节点，看有多少个。

代码：

class Solution {
public:
    int dfs(TreeNode* root, long long targetSum)
    {
        if(root == nullptr)
        {
            return 0;
        }
        int ret = 0;
        if(targetSum - root->val == 0)
        {
            ret++;
        }
        ret += dfs(root->left, targetSum - root->val);
        ret += dfs(root->right, targetSum - root->val);
        return ret;
    }

    int pathSum(TreeNode* root, int targetSum) {
        if(root == nullptr)
        {
            return 0;
        }
        int res = dfs(root, targetSum);
        res += pathSum(root->left, targetSum);
        res += pathSum(root->right, targetSum);
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

方法二：
第二个方法当然是使用前缀和+哈希表算法。
我们边递归边求前缀和，统计的方法还是跟上面一样，这里要注意的是当回溯的时候记住要把当前的位置给去掉（没递归到当前位置的状态）。

代码：

class Solution {
public:
    unordered_map<long long, int> hash;
    int cnt;

    void dfs(TreeNode* root, long long sum, int target)
    {
        if(root == nullptr)
        {
            return;
        }
        sum += root->val;
        cnt += hash[sum - target];
        hash[sum]++;
        dfs(root->left, sum, target);
        dfs(root->right, sum, target);
        hash[sum]--;
    }

    int pathSum(TreeNode* root, int targetSum) {
        hash[0] = 1;
        cnt = 0;
        dfs(root, 0, targetSum);
        return cnt;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

四、总结

我们通过上面的问题可以总结出规律，遇到求连续的和的时候我们就应该想到用前缀和算法，而如果题目只关心次数，不关注具体的解，我们就可以使用（前缀和+哈希表）算法。

---

---