Python的数据科学:8种线性回归的方法以及测量它们的速度_用python构建线性回归

（以下机翻，仅供自己兴趣学习）

在本文中，我们讨论使用 Python 代码/包执行简单线性回归的 8 种方法。我们掩盖了它们的优点和缺点，并展示了它们的相对计算复杂性度量。

对于许多数据科学家来说，线性回归是许多统计建模和预测分析项目的起点。将线性模型（准确且快速）拟合到大型数据集的重要性怎么强调也不为过。正如本文所指出的，线性回归模型中的“LINEAR”术语指的是系数，而不是特征的程度。

特征（或自变量）可以是任何阶数，甚至可以是超越函数，如指数函数、对数函数、正弦函数。因此，即使输出和特征之间的函数关系是高度非线性的，也可以使用这些变换和线性模型对大量自然现象进行（近似）建模。

另一方面，Python 正在迅速崛起，成为数据科学家事实上的首选编程语言。因此，对于数据科学家来说，了解他/她可以快速将线性模型拟合到相当大的数据集并评估每个特征在过程结果中的相对重要性的所有各种方法至关重要。

然而，在Python中进行线性回归分析只有一种方法吗？当有多种方法可供选择时，如何选择最有效的方法？

由于机器学习库 scikit-learn 的广泛流行，一种常见的方法通常是从该库调用线性模型类并拟合数据。虽然这可以提供应用机器学习的其他管道功能（例如数据标准化、模型系数正则化、将线性模型馈送到另一个下游模型）的额外优势，但当数据分析师只需要快速了解数据时，这通常不是最快或最干净的方法。以及确定回归系数的简单方法（以及一些基本的相关统计数据）。

有更快、更干净的方法。但它们可能无法提供相同数量的信息或建模灵活性。

各种线性回归方法的完整样板代码可在我的 GitHub 存储库中找到。其中大多数都是基于 SciPy 包。

SciPy 是基于 Python 的 Numpy 扩展构建的数学算法和便利函数的集合。它通过为用户提供用于操作和可视化数据的高级命令和类，为交互式 Python 会话增添了强大的功能。

让我简要讨论一下每种方法，

Method: Scipy.polyfit( ) or numpy.polyfit( )

这是一个非常通用的最小二乘多项式拟合函数，它接受数据集和任意次数的多项式函数（由用户指定），并返回一个最小化平方误差的系数数组。这里给出了该功能的详细描述。对于简单线性回归，可以选择阶数 1。如果要拟合更高阶数的模型，可以从线性特征数据构造多项式特征并拟合该模型。

Method: Stats.linregress( )

这是 Scipy 统计模块中提供的高度专业化的线性回归函数。它的灵活性相当有限，因为它被优化为仅计算两组测量的线性最小二乘回归。因此，您无法使用它来拟合广义线性模型或多变量回归。但是，由于其特殊性，它是简单线性回归中最快的方法之一。除了拟合系数和截距项外，它还返回 R² 系数和标准误差等基本统计数据。

Method: Optimize.curve_fit( )

这与 Polyfit 方法相同，但本质上更通用。 scipy.optimize 模块中的这个强大函数可以通过最小二乘最小化将任何用户定义的函数拟合到数据集。

对于简单的线性回归，只需编写一个线性 mx+c 函数并调用此估计器即可。不用说，它也适用于多元回归。它返回最小二乘度量最小化的函数参数数组以及关联的协方差矩阵。

Method: numpy.linalg.lstsq

这是通过矩阵分解计算线性方程组最小二乘解的基本方法。它来自 numpy 包中方便的线性代数模块。在底层，它通过计算一个最小化欧氏2-norm || b — a x ||²的向量x来求解方程ax = b。

该方程可能是欠定、良好或过度确定的（即，a 的线性独立行的数量可以小于、等于或大于其线性独立列的数量）。如果 a 是平方且满秩，则 x（除舍入误差外）是方程的“精确”解。

您可以用它进行简单或多变量回归，并返回计算的系数和残差。一个小技巧是，在调用此函数之前，您必须将一列 1 附加到 x 数据以计算截距项。事实证明，这是尝试解决线性回归问题的更快方法之一。

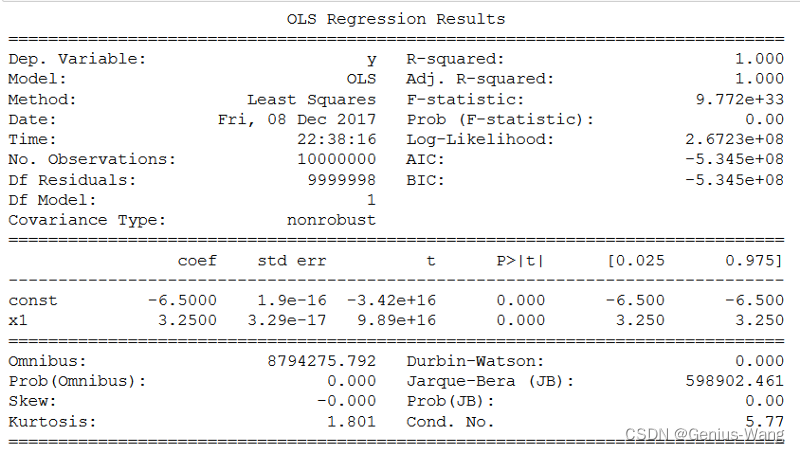
Method: Statsmodels.OLS ( )

Statsmodels 是一个很棒的小型 Python 包，它提供了用于估计许多不同统计模型、以及进行统计测试和统计数据探索的类和函数。每个估算器都有一个广泛的结果统计列表。结果根据现有统计包进行测试，以确保正确性。

对于线性回归，可以使用此包中的 OLS 或普通最小二乘函数，并获得有关估计过程的完整统计信息。

要记住的一个小技巧是，您必须手动向 x 数据添加一个常数来计算截距，否则默认情况下它将仅报告系数。以下是 OLS 模型完整结果摘要的快照。它与 R 或 Julia 等任何函数式统计语言一样丰富。

方法：采用矩阵逆法解析解

对于条件良好的线性回归问题（至少在数据点数量>特征数量的情况下），存在一个简单的封闭式矩阵解决方案来计算保证最小二乘最小化的系数。它由以下给出：

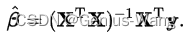
这里讨论了关于这个解决方案的详细推导和讨论。

有两种选择：

(a) 使用简单的乘法矩阵逆。
(b) 首先计算 x 数据的 Moore-Penrose 广义伪逆矩阵，然后与 y 数据进行点积。由于第二个过程涉及奇异值分解（SVD），因此速度较慢，但​​可以很好地处理条件不好的数据集。

Method: sklearn.linear_model.LinearRegression( )

这是大多数机器学习工程师和数据科学家使用的典型方法。当然，对于现实世界的问题，它可能从未被广泛使用，而是被交叉验证和正则化算法（例如 Lasso 回归或 Ridge 回归）所取代。但这些高级功能的本质核心就在于这个模型。

测量这些方法的速度和时间复杂度

作为一名数据科学家，应该始终寻找准确而快速的方法/函数来完成数据建模工作。如果该方法本质上很慢，那么它将为大数据集造成执行瓶颈。

确定可扩展性的一个好方法是运行模型以增加数据集大小，提取所有运行的执行时间并绘制趋势。

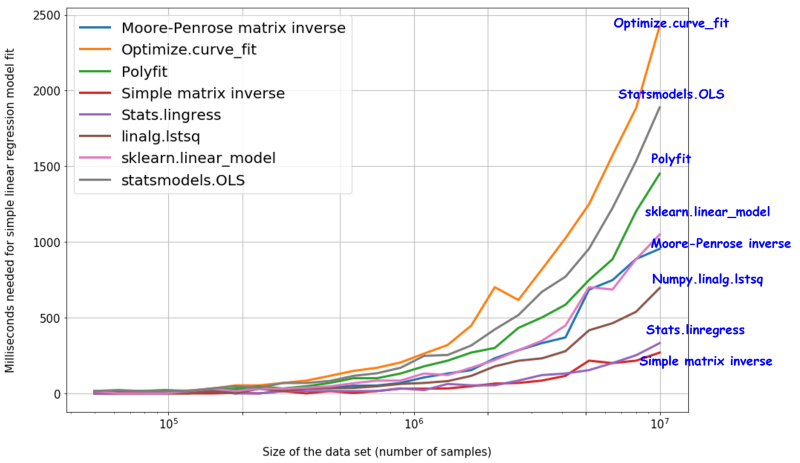
这是相关的样板代码。这是结果。由于其简单性，stats.linregress 和简单矩阵求逆方法速度最快，甚至可以处理多达 1000 万个数据点。

总结

作为一名数据科学家，必须始终探索解决相同分析或建模任务的多种选项，并选择最适合他/她的特定问题的选项。

在本文中，我们讨论了执行简单线性回归的 8 种方法。其中大多数也可以扩展到更广义的多元和多项式回归建模。我们没有列出这些方法的 R² 拟合值，因为它们都非常接近 1。

对于单变量回归，具有数百万个人工生成的数据点，可以很好地估计回归系数。

本文的目的主要是讨论这些方法的相对速度/计算复杂性。我们通过对规模不断增加的合成数据集（最多 1000 万个样本）进行测试，展示了它们各自的计算复杂性度量。令人惊讶的是，与 scikit-learn 广泛使用的线性模型相比，简单的矩阵逆解析解的运行速度相当快。

原文