- 1每周荐书:OpenCV、自然语言、SpringBoot2_springboot2书籍
- 2目标检测算法——YOLOV9——算法详解_yolov9系列算法总结
- 3如何使用 MiniGPT-v2_minigptv2在线使用
- 4下采样是什么_下采样是什么意思
- 5HNU_AI_实验3--分类算法实验
- 6Sqoop测试命令_linux如何测试sqoop是否能够成功连接数据库
- 7快速排序(Java)
- 8鸿蒙开发岗位,面试到底问些啥?_鸿蒙项目面试(1),2024年最新2024历年网易跳动HarmonyOS鸿蒙面试真题解析_hongmeng面试题
- 9Access,Mysql数据库速度测试_access的处理速度
- 10怎么部署个人云服务器?保姆级教程_部署私人服务 什么方式最好
算法之股票最佳时机系列问题(一次搞定6道股票问题)_股票问题算法
赞
踩
简述
本文旨在总结leetcode中遇到的一系列股票问题,分别详细阐述解决方法和各问题之间的区别。
目录
- 1. T121 买卖股票的最佳时机 简单
- 2. T122 买卖股票的最佳时机 II 简单
- 3. T123 买卖股票的最佳时机 III 困难
- 4. T188 买卖股票的最佳时机 IV 困难
- 5. T309 最佳买卖股票时机含冷冻期 中等
- 6. T714 买卖股票的最佳时机含手续费 中等
以上题目均来自leetcode
题目
1. 买卖股票的最佳时机
题目描述
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票一次),设计一个算法来计算你所能获取的最大利润。
注意:你不能在买入股票前卖出股票。
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
算法
这道题由于只能进行一笔交易,因此只要选择最低的买点和最高的卖点,就可以获得最大的收益。
(1) 暴力法
最容易想到的暴力穷举法,从前往后遍历price,对于当前的prices[i],和i之前的所有价格进行比较,记录最大的收益。
代码如下:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
ans = 0
for i in range(1, n):
for j in range(i):
ans = max(ans, prices[i]-prices[j])
return ans
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
该算法的时间复杂度是O(n^2),在leetcode上最后一个测试过不了超时了,于是我们想想更优的算法。
(2) 一次遍历
前面我们提到了,我们的买点必须是当前时刻之前的最低价格,于是我们可以在遍历prices的时候记录下之前的最低股价,如果当前价格低于最低股价,则更新最低股价;如果高于最低股价,则更新收益。
代码如下:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
n = len(prices)
min_price = prices[0]
ans = 0
for i in range(1, n):
if prices[i] < min_price:
min_price = prices[i]
else:
ans = max(ans, prices[i]-min_price)
return ans
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
由于只有一次遍历,因此时间复杂度为O(n),空间复杂度为O(1)。
这道题还可以用单调栈来解答,针对单调栈,我会重新写一篇文章来详细探讨。
2. 买卖股票的最佳时机 II
题目描述
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
算法
这道题和前一道题不同之处在于可以进行多次交易。
(1) 动态规划
class Solution:
def maxProfit(self, prices: List[int]) -> int:
"""
dp[i][j]
j: 0 没有持有 1 持有
"""
n = len(prices)
dp = [[0] * 2 for _ in range(n)]
dp[0][1] = -prices[0]
for i in range(1, n):
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
return dp[-1][0]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
时间空间复杂度都为O(n)。
(2) 峰谷法
对于数组[7, 1, 5, 3, 6, 4],绘制在图上如下:
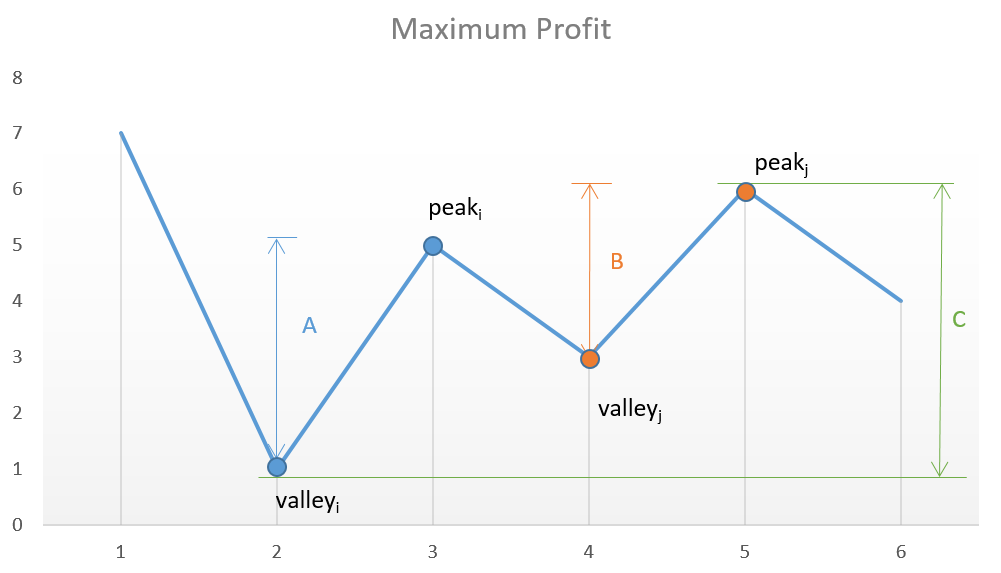
我们想要最大化利润,其实就是在每一个波谷买入,每一个波峰卖出。这就是股市中所谓的“高抛低吸”,如果我们试图跳过一个波峰来获取更大的收益,那么会错过一笔交易,从而导致总利润减少。
代码如下:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
ans = 0
i = 0
while i < len(prices) - 1: # 由于我们比较的是i和i+1,所以只需要遍历到n-2
# 寻找波谷
while i < len(prices) - 1 and prices[i] >= prices[i+1]:
i += 1
valley = prices[i]
# 寻找波峰
while i < len(prices) - 1 and prices[i] <= prices[i+1]:
i += 1
peak = prices[i]
ans += peak - valley
return ans
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
由于只进行一次遍历,因此时间复杂度为O(n)
(3) 简化
在上述解法中,我们考虑波谷买入,到了波峰才卖出。
我们换一种思路,我们虽然在波峰才卖出,但是在股价爬坡时期的每一天,我们都计算一下当前获得了多少收益,将每天获得的收益加起来,就是波峰卖出时这一阶段获得的收益。
如下图所示数组[1, 7, 2, 3, 6, 7, 6, 7],我们在第3天以2元买入,第4天股价3,收益1,总收益1;第5天股价6,收益3,总收益4;第6天股价7,收益1,总收益5。这种每天计算收益的方式和一次性波峰波谷计算的方式7-2=5相等。
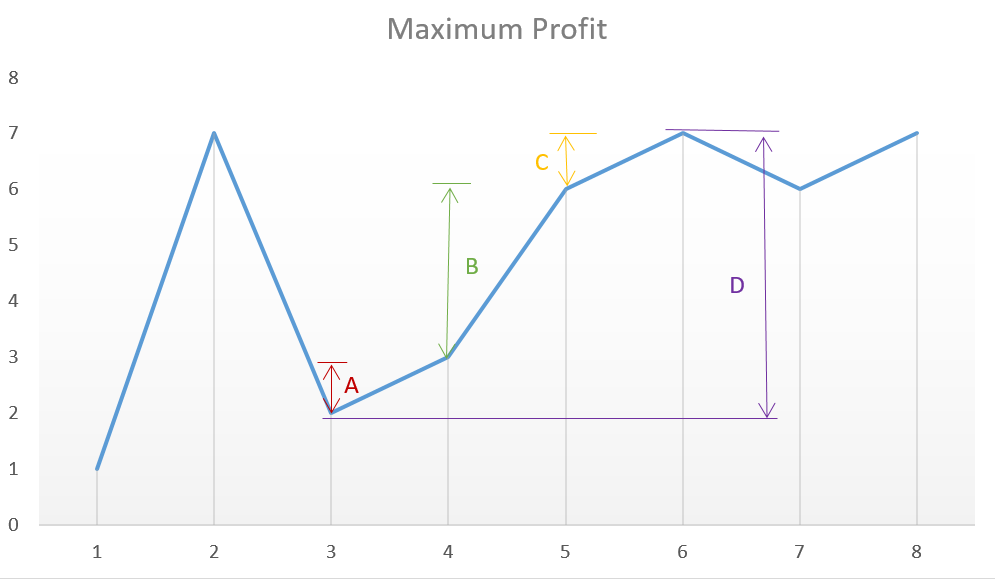
代码如下:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
ans = 0
for i in range(len(prices)-1):
diff = prices[i+1] - prices[i]
if diff > 0:
ans += diff
return ans
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
时间复杂度O(n),空间复杂度O(1)
3. 买卖股票的最佳时机 III
题目描述
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [3,3,5,0,0,3,1,4]
输出: 6
算法
这道题和第一题的不同之处在于最多可以进行两次交易。
刚接触到这道题,要求最多两笔交易,似乎无从下手。我们把问题分解一下,能不能分解成两次交易,并让两次的利润和最大呢?答案是可以的,我们可以在第一题的基础上,再进行一次交易,从而实现最大利润和。这样做的关键是如何确保两次交易不会重合呢?
用一个数组first_trade存储一次交易获得的最大利润,first_trade[i]表示i时刻能获得的最大收益,first_trade[-1](数组最后一个元素)就是第一题的答案。
得到first_trade数组之后,我们再从prices的末尾向前遍历一遍,记录遍历过程中的最大股价max_price,用max_price减去当前i时刻的股价prices[i],再加上前一时刻的最大利润first_trade[i-1],即:max_price-prices[i]+first_trade[i-1],就可以得到当前时刻的两次交易的最大收益。
代码如下:
- python
class Solution: def maxProfit(self, prices: List[int]) -> int: if not prices: return 0 n = len(prices) first_trade = [0] * n min_price = prices[0] # 计算一次交易的最大利润,存入first_trade数组 for i in range(1, n): first_trade[i] = max(first_trade[i-1], prices[i] - min_price) min_price = min(min_price, prices[i]) max_price = prices[-1] res = first_trade[-1] # 计算两次交易的最大利润和 for i in range(n-1, 0, -1): if prices[i] < max_price: res = max(res, max_price - prices[i] + first_trade[i-1]) else: max_price = prices[i] return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- java
public class Solution { public int maxProfit(int[] prices) { int n = prices.length; int[] record = new int[n]; int profit = 0, min = prices[0]; for (int i = 1; i < n; i++) { if (prices[i] < min) { min = prices[i]; } profit = Math.max(profit, prices[i] - min); record[i] = profit; } int max = prices[n - 1], res = record[n - 1]; for (int i = n - 2; i > 0; i--) { if (prices[i] > max) { max = prices[i]; } res = Math.max(res, record[i-1] + max - prices[i]); } return res; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
由于遍历两次,时间复杂度为O(2n)≈O(n),存储数据用到了fist_trade数组,长度为n,因此空间复杂度为O(n)。
4. 买卖股票的最佳时机 IV
题目描述
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [2,4,1], k = 2
输出: 2
算法
这道题目是上一道题目更加泛化的版本,从k=2到k为任意数。
动态规划
对于交易的每一天,涉及到多种状态,包括:第几天、交易几笔、持有的股票数(0或者1),可以用三维动态规划来完成。
我们用一个三维n*k*2的矩阵dp来存储数据,第一维n表示第几天,第二维k表示进行了k笔交易,第二维0或者1表示手里持有的股票数。
对于任意一个数dp[i][j][0],表示第i天进行了j笔交易,手中没有股票时的利润,我们可以得到:
d
p
[
i
]
[
j
]
[
0
]
=
m
a
x
(
d
p
[
i
−
1
]
[
j
]
[
0
]
,
d
p
[
i
−
1
]
[
j
]
[
1
]
+
p
r
i
c
e
s
[
i
]
)
dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j][1] + prices[i])
dp[i][j][0]=max(dp[i−1][j][0],dp[i−1][j][1]+prices[i])
d
p
[
i
]
[
j
]
[
1
]
=
m
a
x
(
d
p
[
i
−
1
]
[
j
]
[
1
]
,
d
p
[
i
−
1
]
[
j
−
1
]
[
0
]
−
p
r
i
c
e
s
[
i
]
)
dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0] - prices[i])
dp[i][j][1]=max(dp[i−1][j][1],dp[i−1][j−1][0]−prices[i])
以上便是状态转移方程。
为了求解动态规划,我们还需要初始状态:
d
p
[
0
]
[
j
]
[
0
]
=
0
dp[0][j][0] = 0
dp[0][j][0]=0
d
p
[
0
]
[
j
]
[
1
]
=
−
p
r
i
c
e
s
[
0
]
dp[0][j][1] = -prices[0]
dp[0][j][1]=−prices[0]
上式表示在第1天的时候,如果手里没有持有股票,则利润为0;如果持有1只股票,则利润为-prices[0]。不要担心利润为负数,因为在卖出股票后会加上price,则就获得了正的利润。
疑问
为什么针对所有的j都需要设置为 d p [ 0 ] [ j ] [ 1 ] = − p r i c e s [ 0 ] dp[0][j][1] = -prices[0] dp[0][j][1]=−prices[0],而不是 d p [ 0 ] [ 1 ] [ 1 ] = − p r i c e s [ 0 ] dp[0][1][1] = -prices[0] dp[0][1][1]=−prices[0]?
因为给定的case,不一定能够完成k次交易,然而最后返回的结果是 d p [ n − 1 ] [ k ] [ 0 ] dp[n-1][k][0] dp[n−1][k][0]。假如只能完成一次交易,那最终的结果是从 d p [ i ] [ k − 1 ] [ 0 ] dp[i][k-1][0] dp[i][k−1][0]开始进行转移的。
另外还有一个注意的地方,我们知道对于长度为length的prices,最多可以进行length//2次交易,leetcode上的测试用例里会出现k非常大的情况,如果不对非常大的k进行处理,那么初始化dp矩阵时会消耗非常大的内存和时间,因此会不通过。
当k>=length//2时,相当于没有了k的限制,就回归到问题二,因此在这种条件下我们可以复用问题二的代码。
代码如下
- python
class Solution: def maxProfit(self, k: int, prices: List[int]) -> int: n = len(prices) if n < 2: return 0 if k > n / 2: return self.maxProfit_with_no_k_limit(prices) dp = [[[0] * 2 for _ in range(k+1)] for _ in range(n)] for i in range(n): for j in range(1, k+1): if i == 0: # 初始状态 dp[i][j][0] = 0 dp[i][j][1] = -prices[0] else: # 状态转移 dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j][1] + prices[i]) dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0] - prices[i]) return dp[n-1][k][0] # 问题二代码,只是换了一个方法名 def maxProfit_with_no_k_limit(self, prices: List[int]) -> int: ans = 0 for i in range(len(prices)-1): diff = prices[i+1] - prices[i] if diff > 0: ans += diff return ans
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- java
public class Solution { public int maxProfit(int k, int[] prices) { int n = prices.length; if (n <= 1) { return 0; } if (k > n / 2) { return getProfitNoKLimit(prices); } int[][][] dp = new int[n][k + 1][2]; // 设置初始状态 for (int j = 1; j <= k; j++) { dp[0][j][1] = -prices[0]; } for (int i = 1; i < n; i++) { for (int j = 1; j <= k; j++) { dp[i][j][0] = Math.max(dp[i-1][j][0], dp[i-1][j][1] + prices[i]); dp[i][j][1] = Math.max(dp[i-1][j][1], dp[i-1][j-1][0] - prices[i]); } } return dp[n-1][k][0]; } private int getProfitNoKLimit(int[] prices) { int profit = 0; for (int i = 1; i < prices.length; i++) { if (prices[i] > prices[i-1]) { profit += (prices[i] - prices[i-1]); } } return profit; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
时空复杂度分析
两层n和k的循环,因此时间复杂度是O(kn)
由于我们使用n*k*2三维矩阵存储数据,空间复杂度为O(2kn)≈O(kn)
5. 最佳买卖股票时机含冷冻期
题目描述
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
示例:
输入: [1,2,3,0,2]
输出: 3
算法
动态规划
我们继续沿用动态规划的思想,相比上一道题,由于不限制交易次数,因此少了一维k。
定义dp[i][0]表示第i天没有持有股票,dp[i][1]表示第i天没有持有1只股票。
由于有1天的冷冻期,因此如果第i天买入股票,需要满足第i-1天和i-2天的股票数都是为0。
这样就满足i-1天是冷冻期了。
因此状态转移方程:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
初始状态:
dp[0][1] = - prices[0]
代码如下:
- python
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
dp = [[0] * 2 for _ in range(n+2)]
for i in range(2, n+2):
if i == 2:
dp[i][1] = - prices[i-2]
else:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i-2])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i-2])
return dp[n+1][0]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
说明:由于当前i状态需要用到i-2时的状态,因此我们把dp数组长度定义为n+2,从2开始遍历,这样方便处理边界情况,而取prices的值的时候第i时刻取prices[i-2].
- java
public class Solution { public int maxProfit(int[] prices) { int n = prices.length; if (n < 2) { return 0; } int[][] dp = new int[n][2]; dp[0][1] = -prices[0]; for (int i = 1; i < n; i++) { dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]); if (i > 1) { dp[i][1] = Math.max(dp[i - 1][1], dp[i - 2][0] - prices[i]); } else { dp[i][1] = Math.max(dp[i - 1][1], -prices[i]); // 因为i=1,就不需要看i-2 } } return dp[n-1][0]; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
时空复杂度分析
一次遍历,因此时间复杂度为O(n)
所用数组长度为n+2,因此空间复杂度为O(n)
6. 买卖股票的最佳时机含手续费
题目描述
给定一个整数数组 prices,其中第 i 个元素代表了第 i 天的股票价格 ;非负整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每次交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
示例 1:
输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
输出: 8
算法
动态规划
继续沿用动态规划的思想,我们在每次状态的股票数由1向0转移的时候在利润中减去fee。
状态转移方程:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i] - fee)
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
初始状态:
dp[0][1] = -prices[0]
代码如下:
class Solution:
def maxProfit(self, prices: List[int], fee: int) -> int:
n = len(prices)
dp = [[0] * 2 for _ in range(n)]
for i in range(n):
if i == 0:
dp[i][1] = -prices[0]
else:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i] - fee)
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
return dp[n-1][0]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
时间复杂度:O(n)
空间复杂度:O(n)
简化动态规划
分析上面的算法我们可以知道,当前状态只和上一个状态有关,因此不必维护一个数组。
我们维护两个变量cash和hold,分别表示不持有股票和持有股票的最大利润。
状态转移为:
cash = max(cash, hold + prices[i] - fee)
hold = max(hold, cash - prices[i])
代码如下:
- python
class Solution:
def maxProfit(self, prices: List[int], fee: int) -> int:
cash, hold = 0, -prices[0]
for i in range(1, len(prices)):
cash = max(cash, hold + prices[i] - fee)
hold = max(hold, cash - prices[i])
return cash
- 1
- 2
- 3
- 4
- 5
- 6
- 7
说明:由于最后肯定要把股票全部卖掉,所以返回cash
- java
class Solution {
public int maxProfit(int[] prices, int fee) {
int n = prices.length;
if (n < 2) {
return 0;
}
int buy = -prices[0] - fee, sell = 0;
for (int i = 1; i < n; i++) {
int tmp = sell;
sell = Math.max(sell, buy + prices[i]);
buy = Math.max(buy, tmp - prices[i] - fee);
}
return sell;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
时间复杂度:O(n)
空间复杂度:O(1)



