vslam论文17：基于UWB测量的高效平面位姿估计（ICRA 2023）_uwb相关毕设

摘要

       状态估计是自主系统的重要组成部分。集成超宽带(UWB)技术已被证明可以纠正长期估计漂移并绕过环路闭合检测的复杂性。然而，很少有机器人工作将超宽带作为一个独立的状态估计解决方案。

       这项工作的主要目的是研究仅使用超宽带距离测量的平面姿态估计。我们证明了一个两步格式的优良性质，即我们可以通过一步的高斯-牛顿迭代使一个一致估计量渐近有效。基于这一结果，我们设计了GN-ULS估计器，与以前的方法相比，它大大减少了计算时间，并提供了仅使用超宽带进行实时状态估计的可能性。

I. 引言

A. 背景

       状态估计是智能移动机器人实现避障、路径规划等任务的基本前提。近年来，人们一直致力于利用车载传感器(如IMU、摄像头和激光雷达)实现高性能和实时状态估计。然而，这些方法面临着诸如长期漂移[1]和在几何退化环境中的低鲁棒性[2]等问题。为了克服上述挑战，我们可以将GPS等外部信息整合到状态估计中[3]。

       超宽带(UWB)是一种对多径效应具有鲁棒性的无线电技术，可以提供精确的TOA或TDOA测量[4]。传统上，超宽带用于定位[5]-[9]，而最近的许多研究[10]-[13]将超宽带集成在一起，实现了gps拒绝环境下的无漂移状态估计，但很少有机器人研究独立使用超宽带进行姿态估计。

       这项工作考虑仅通过使用对称双向TOA测量技术获得的超宽带范围测量来估计机器人的姿态。我们关注的是如图1所示的平面情况，它有许多关键的应用如搜救机器人和室内服务机器人。我们将其称为信号处理界的刚体定位问题(RBL)。

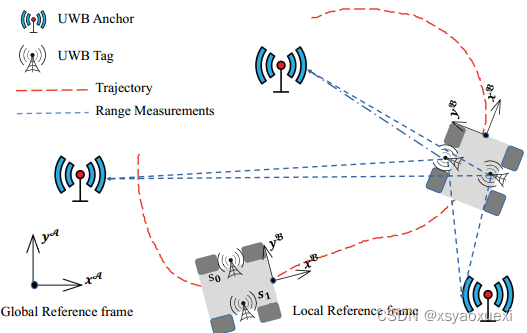
图1: 基于UWB测量的平面位姿估计

       通过文献综述，我们发现姿态估计器的统计效率没有得到很好的研究，并且估计器的计算复杂度需要进一步降低才能实现实时估计。在这项工作中，我们采用两步格式并开发了一个封闭形式的估计量，该估计量在与锚形有关的温和条件下是渐近有效的，并且大大减少了计算时间。我们还进行了模拟和实验，以证明我们的方法的统计和计算效率。

B. 平面刚体定位相关工作

       在高斯噪声假设下，RBL的最大似然(ML)公式是一个受限加权最小二乘(LS)问题（2）。然而，由于(2)的非凸性和非线性，很难获得ML估计。一种常见的做法是将最小二乘方法应用于平方距离测量并制定平方最小二乘(SLS)问题(6)。

       据我们所知，文献首次提出了RBL问题，提出通过将测量的平方投影到单位向量的零空间来修正SLS问题。这种运算消除了二次项，使问题线性化，这一思想被作品[17]和我们的作品所遵循。我们将所得公式(7)命名为投影平方最小二乘(PSLS)。基于PSLS的工作[16]用高斯-牛顿算法求解了一个加权正交Procrustes问题，并从更简单的闭型解问题中得到初值。该工作[16]还导出了单约束Cramer-Rao下界(CRLB)。文献[17]利用旋转矩阵的结构，提出了一个广义信赖域子问题(GTRS)，并对其解进行了细化线性SLS问题。文献[18]采用半定松弛，将SLS表述为半定规划(半定规划)。

该方法通过对ML问题进行一步高斯-牛顿迭代来改进。

       综上所述，平面RBL问题的ML估计很难得到。以前的工作转向SLS问题，并使用不同的技术使问题线性化。然而，早期的研究并没有严格评估所提出的估计器与ML估计器的偏差或它们的统计效率。考虑到人们对可证明的最优状态推理越来越感兴趣，我们认为这些主题值得仔细研究。理论结果也激励了更快的最优估计器的设计。

我们总结了我们的贡献如下:

(1)我们设计了一个仅使用UWB距离测量的封闭形式平面姿态估计器，其计算复杂度为0 (n)，并且随着测量次数n的增加可证明收敛于ML估计器。鉴于实际UWB系统的高采样率，我们的工作可以在应用中发挥有价值的作用。

(2)我们提出了与锚形几何相关的温和条件，在此条件下ML估计量，因此我们的方法是渐近有效的，即估计可以以最小方差收敛到真实姿态。

(3)在室内环境下进行实验，详细阐述数据预处理流程。数据集和代码可以在我们的网站上找到。

II. 平面刚体定位

A. 测距模型

       设A为整体框架，设B为刚体的局部框架。A和B的z轴是对齐的。我们用表示第m个锚点与第i个标签之间的距离测量值，用表示第m个锚点与第i个标签之间的高度差。距离测量模型如下:

 B. 假设 

我们做了以下假设:

假设1:锚和标签高度相同。

       注1:为简单起见，我们假设∆him = 0，对∆him = 0的修改详见附录1。

假设2:rim是均值为零、有限且已知标准差σim > 0的i.d高斯噪声。

假设3:序列a a1,a a2，…的样本分布Fm收敛于某个分布Fµ。

例1:假设a am是分布函数Fµ的独立样本，随着m的增大，Fm收敛于Fµ。

例2:随着重复测距次数T的增加，Fm收敛于Fµ。表示由F引起的度量，当m = 1，…，m时，我们有。

假设4:至少存在三个非共线锚点，且至少有两个标签与局部参照系原点ob非共线。

       注2:平面位姿可观测的充要条件是至少有三个非线性锚点和至少两个标签。附录A给出了一个简单的证明。在特定的约束条件下，所需的传感器可以进一步减少，如在work[21]中。为了简化附录C中引理1的证明，我们在本文中做了一个稍强的假设。

假设5:考虑假设3中的极限测度µ，不存在任何直线L使得µ(L) = 1。

C. 最大似然公式

平面RBL问题的ML估计是以下优化问题的解:

 D. 平方最小二乘公式

ML公式是非线性的，非凸的，难以求解。我们将(1)两边平方，得到:

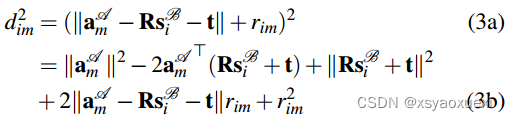
 III. 一种高效的平面位姿估计器

基于以下定理，我们分两步设计平面姿态估计器:

       定理1:假设R和t是R和t的n个一致估计。在ML问题(2)上通过一步高斯-牛顿迭代得到的估计值，随着测量数n的增加，在概率上收敛于ML估计值

 A. 无约束的最小二乘问题

       表示上的投影矩阵为。式(5)的两边同时乘以P，消去二次项，我们得到如下问题[16]:

        引理1:假设4下，设计矩阵H = [H1Γ，H2]为满列秩，由此得到的LS问题的唯一解为:

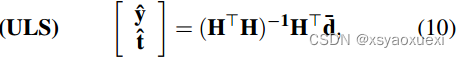
 定理2:ULS估计量是√n一致的，即:

       注意，从(10)中估计的y不受单位长度的约束，因此我们进一步将投影到so(2)上。 

将任意矩阵X∈映射到SO(2)上的矩阵投影π定义为

定理3:由(11)生成的投影估计是√n一致的，即 

B.高斯-牛顿迭代的一步 

       在第一步给出一个√n一致估计的情况下，我们对ML问题(2)实现了一步高斯-牛顿迭代，得到了GN-ULS估计量。利用式(8)，我们可以将问题(2)转化为无约束问题:

 我们总结了算法1中的GN-ULS估计器。

 IV. 统计效率分析

       根据定理1，随着n的增加，GN-ULS估计收敛于ML估计。下面的定理描述了GN-ULS估计器的统计效率。定理4:在假设3-5下，ML估计，因此GN-ULS估计是渐近有效的，即随着测量数n的增加，

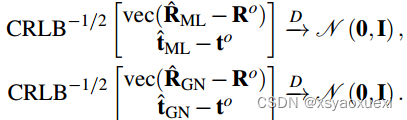
       备注5:该定理建立了所提估计量的最优性，并使我们可以利用CRLB近似估计协方差，这是传感器融合方案中的一个关键问题。虽然我们需要真实姿态来计算CRLB，但我们可以合理地使用作为替代方案。

 V. 仿真与讨论

       我们通过比较均方根误差(RMSE)与下界(即CRLB轨迹的平方根，记为√CRLB)来验证所提出的GNULS估计量的渐近效率。我们与之前的文献[17]和[18]进行比较，分别记为GTRS和GN-SDP。我们还比较了先对标签进行本地化的分治方法。为了实现这个称为DAC的估计器，我们遵循工作进行定位，并解决姿态估计的最小二乘问题。给定一个√MT−一致的位置估计量，这个DAC估计量可以被证明是√n−一致的，详见附录F。

A. 仿真设定

       在我们的模拟中，在全局框架中，有M = 3个锚点部署在[50,0]、[50,50]和[0,50]上。在局部帧中，有N = 2个标签部署在[3,0]和[3,3]处。

真正的姿势是t o = [0,25]， θ o = 60◦。

       我们对每个设置运行L = 1000蒙特卡罗实验，并报告平均结果。我们使用弦距[25]来计算旋转矩阵的RMSE: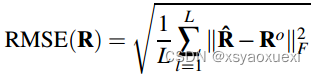

 B. 仿真结果

1)重复测距下的渐近效率:

       增加重复测距的次数T。噪声标准差σmi设为0.05[1,2,3,4,5,6]。如图2a所示，ULS估计器和DAC估计器是√n−一致的，但不是渐近有效的。GTRS估计器在大样本下偏离下界，主要原因是估计在SLS问题(6)上得到了改进，而在ML问题(2)上没有得到改进。GNULS和DAC估计器的效率明显更高复杂度为0 (n)，如图2b所示。构建GN-ULS和GN-SDP估计器的优化问题同样需要O(n)的计算，但解决这些问题占据了计算成本的大头。

图2:重复测距时的性能。(a)不同姿态估计量的RMSE及随重复测距次数T增加的下界。(b)不同姿态估计器随T增加的平均计算时间。

2)多锚点下的渐近效率:

       我们在模拟平面上均匀地部署新的锚点。标准差σim设置为0.1。如图3a所示，GTRS估计量偏离下界。当我们部署10000个锚点时，MATLAB CVX工具箱将SDP问题报告为不可行的。在非常小的噪声下，图3b也出现了同样的失稳问题。

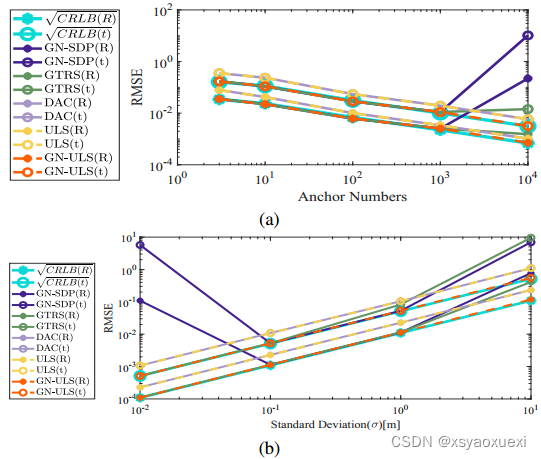
图3:多个锚点及不同噪音水平下的表现。(a)不同姿态估计量的RMSE及锚点个数增加时的下界。

(b)不同位姿估计量的RMSE及随标准差增大的下界。

3)大噪声下的渐近效率:

       我们将标准差σim从0.01调整到10，设T = 1000。如图3b所示，GTRS和GN-SDP在大鼻子下偏离下界，这是因为它们在(3b)中忽略了r²m，并使用噪声测量来计算协方差矩阵。

C. 讨论

       仿真结果表明，GN-ULS达到了理论下界，在稳定性和精度上都优于计算更复杂的估计器。由定理1可以保证，经过高斯-牛顿一步改进的DAC估计器可以达到与GN-ULS相当的性能。但DAC估计器似乎对动态实验中的异常值更敏感，如第六节所示。

VI. 实验

A. 系统概述

       图4为总体积为10m × 6m × 4m的实验系统及环境。该系统由运动捕捉系统(OptiTrack: X22)、超宽带(NoopLoop: LinkTrack)、Ackerman台车平台和嵌入式处理器(NVIDIA: TX2)组成。我们使用碳纤维立方体框架，而不是直接使用手推车作为刚体，以避免阻塞超宽带信号。三个超宽带标签固定在立方体上，其高度与环境中部署的八个锚点大致相同。

 图4:实验设置

B. 数据收集

我们把动作捕捉帧称为全局帧。

       UWB测距频率为100Hz，运动捕捉系统提供120Hz的姿态地面真实度，声称精度为±0.15毫米和±0.5度2。在实验过程中，NVIDIA-TX2通过其串口解包UWB数据，并通过TCP采集运动捕捉系统数据。在动态数据集中，我们使用TX2和执行插值，使运动捕捉测量值与超宽带测量值对齐。

C.UWB校准

UWB测距测量实际建模为:

       其中f(d o)是距离相关偏差，e是零均值高斯噪声。我们将小车静止一段时间，并使用样本方差来估计e的标准差。更苛刻的任务是校准f(d o)，我们假设f(d o)是d o的线性函数[26]。我们控制小车在环境中移动，收集标定数据集，并使用最小二乘法拟合f(d o)。考虑到室内复杂的通信环境，我们在校准前进行了异常值抑制。与[6]、[13]中的方法类似，如果将瞬间t的距离测量作为离群值拒绝

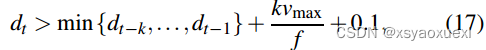
 D.静态数据集和姿态估计结果

       我们将小车放置在7个不同的位置，并以大约60°的间隔从0°到300°改变方向。我们总共收集了42个静态数据集，每个数据集持续大约100秒。我们计算所有数据集的均方根误差，并比较平均结果。我们选择两个标签和三个锚，并使用厘米和度作为图5的单位。结果表明，所有方法都达到了与地面真值系统相似的精度。

 图5:重复测距下的静态实验

E.动态数据集和姿态估计结果

       我们控制小车以不同的速度(0.49m/s, 0.23m/s和0.11m/s)移动，并收集快速，中速和慢速数据集。当出现异常值时，我们实现插值以提供实时估计。在动态情况下使用重复测量是不合理的。相反，我们采用所有三个标签和八个锚。

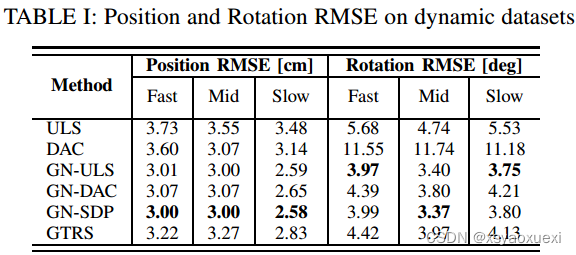
       图6显示了快速数据集上的结果，其中GN-ULS使用8个锚点和3个标签之间的24个范围测量实现了平均RMSE为3.97度和3.01厘米。表1总结了三个数据集的总体结果，其中GN-DAC表示基于DAC估计器的高斯-牛顿迭代的一步。

 F. 讨论

       假设噪声的标准偏差在一厘米量级，所有比较的方法在实验中都达到了相似的精度。然而，GN-ULS和GNDAC估计器显著减少了计算时间。我们将这种优势归因于定理1提供的洞察力。我们还注意到，DAC估计器对异常值的鲁棒性不如ULS估计器估计器在动态数据集上的性能不如在静态数据集上。主要原因是复杂的室内环境，在不同的位置和方向上，由于墙壁的阻碍和信号反射，距离相关偏置f(d)会发生变化。