Trie树（详解+例题）

1、介绍Trie树

Trie树，即字典树，又称单词查找树或键树，是一种树形结构，每个节点保存一个字符，一条路径表示一个字符串。
   它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较。

Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

2、应用及基本性质

• 要么存储小写字母/大写字母

• 要么存储数字

• 要么存储0或1

• 不会出现混着存的情况（比如：既存大写字母又存小写字母还存数字这种）

1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符。

2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。

3. 每个节点的所有子节点包含的字符都不相同。

3、实现

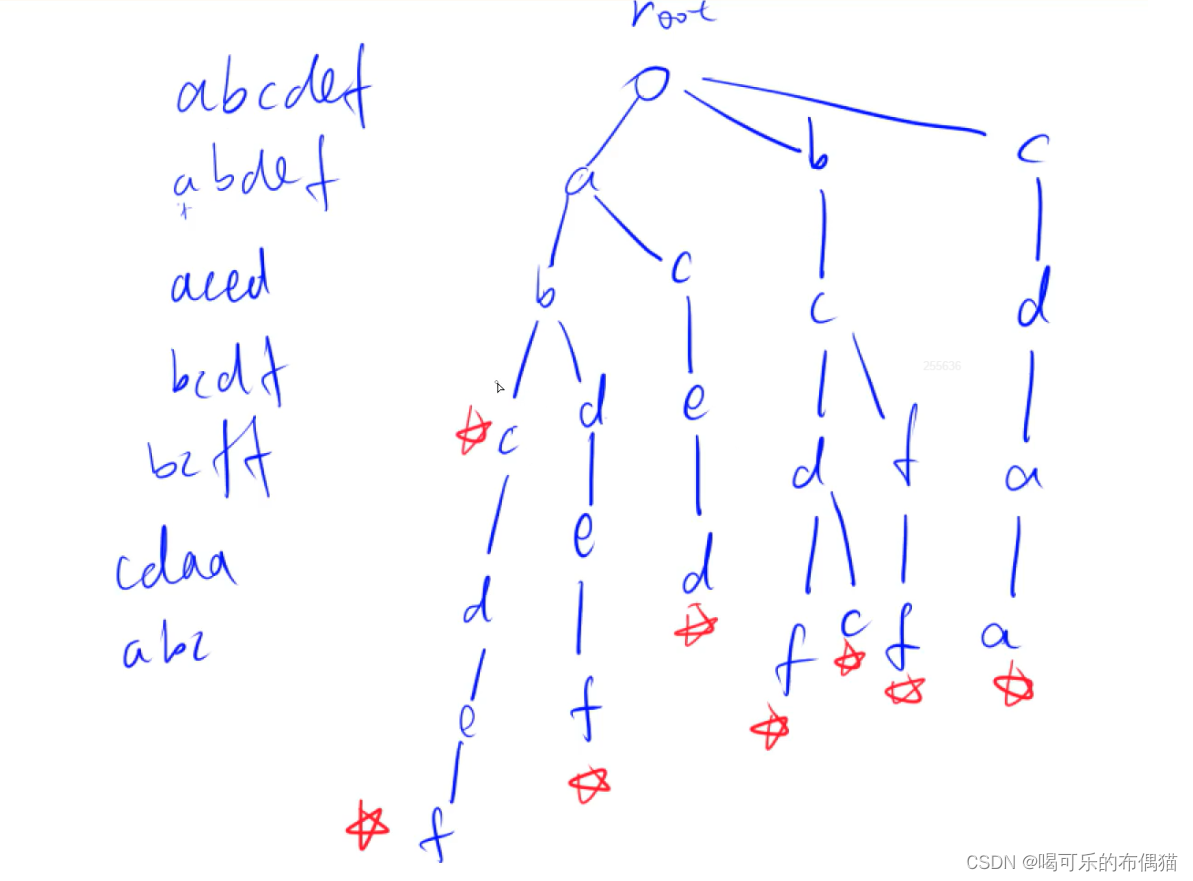
• 根据上述例子：过程如下(以abcdef，abdef，abc为例子)其他同理

• 首先创建根节点root，刚开始根节点不存在a，所以创建a节点

• 接着往下走，在a节点下插入字符b，节点a下不存在子节点b，创建节点b。

• 继续走，在b节点下插入字符c，节点b下不存在子节点c，创建节点c。

• 接着上述过程（假设创建到最后一个），我们创建到了f节点，此字符串结束，在末尾做一个标记，插入字符串abcdef完成

• ---

• 再插入字符串abdef

• 首先插入a节点，发现root下有子节点a，所以不用创建，继续。

• 插入字符b节点，发现a下有子节点b，所以不用创建，继续。

• 插入字符d节点，发现b下没有子节点d，所以创建d子节点，继续。

• 插入字符e节点，发现d节点下没有子节点e，所以创建子节点e，继续。

• 插入字符f节点，发现e节点下没有子节点f，所以创建子节点f，继续。

• 插入结束，在字符串结尾做一个标记，表示完成插入字符串

• ---

• 插入abc

• 首先插入a节点，发现root下有a节点，所以不用创建，继续。

• 再插入b节点，发现a节点下的子节点也有b，所以不用创建，继续。

• 再插入c同样，发现b节点下的子节点有c，所以不用创建，完成 插入，做一个标记。

---

3.1、代码模板

int idx; //各个节点的位置，编号
int son[N][26]; //trie树
int cnt[N];//标记以某个编号结尾的单词的个数
//插入
void insert(string s)
{
    int p = 0; //刚开始指向根部节点（root）
    for(int i=0;i<s.size();i++)
    {
        //将字母映射成数字（a->0,b->1,c->2）依次类推z->25;
        int u = s[i] - 'a';
        //如果当前没有此节点，创建这个节点，分配位置（编号）
        if(!son[p][u]) son[p][u] = ++idx; //新节点的编号是idx+1
        p = son[p][u];
    }
    cnt[p]++;
}
//查找单词操作
int query(string s)
{
    int p = 0; //指向根节点
    for(int i=0;i<s.size();i++)
    {
        //将当前字符转换成数字（a->0, b->1,...）
        int u = s[i] - 'a';
        //如果走不通了，即树中没有保存当前字符
        //则说明树中不存在该字符串
        if(!son[p][u]) return 0;
        p = son[p][u];//指向下一个节点
    }
    //循环结束的时候，p 等于字符串 s 的尾字符所对应的 idx
    // cnt[p] 就是字符串 s 出现的次数
    return cnt[p];
}

---

4、例题835. Trie字符串统计 - AcWing题库

 

---

AC代码：

#include<iostream>
#include<cstring>
 
using namespace std;
 
const int N = 1e5;
int idx;
int son[N][26];
int cnt[N];
 
//插入
void insert(string s)
{
    int p = 0;//指针指向
    for(int i=0;i<s.size();i++)
    {
        int u = s[i] - 'a'; //映射
        //如果不存在该节点，创建一下
        //新节点编号idx+1
        if(!son[p][u]) son[p][u] = ++idx;
        p = son[p][u];//指向下一个节点
    }
    cnt[p]++;
}
 
//查找
int query(string s)
{
    int p = 0;
    for(int i=0;i<s.size();i++)
    {
        int u = s[i] - 'a';
        if(!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}
 
int main()
{
    int n;
    scanf("%d", &n);
    while(n --)
    {
        string op,str;
        cin >> op >> str;
        if(op == "I")
        {
            insert(str);
        }
        else if(op == "Q")
        {
            int res = query(str);
            cout << res << endl;
        }
    }
    return 0;
}