筛选质数的三种方法方法_质数筛选法

---

筛选质数的方法

质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

（1）朴素筛法(时间复杂度O(n))

将比自己小的数字并且大于1的数枚举出来，看看能不能除余，这个是我们最除学筛质数的方法，比较的好理解，我们直接上代码：

#include<bits/stdc++.h>
using namespace std;

bool cheak(int x)
{
    if(x<=1) return false;
    if(x==2) return true;
    for(int i = 2;i < x;i ++ )
    {
        if(x%i==0) return false;
    }
    return true;
}
int main()
{
    int n;
    cin >> n;
    while(n--)
    {
        int x;
        cin >> x;
        if(cheak(x)) cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

朴素筛法的优化：（时间复杂度优化到O(sqrt(n)）

实际上，对于任何一个数n，我们如果有两个数a，b（a，b>=2 && a,b<n)有ab==c，我们只需要将i枚举到a，也就是 i<n/b,

但是对于b来说一定比i大，所以我们只需要枚举到i<n/i.

bool cheak(int x)
{
    if(x<=1) return false;
    if(x==2) return true;
    for(int i = 2;i <= x/i;i ++ )
    {
        if(x%i==0) return false;
    }
    return true;
}
1
2
3
4
5
6
7
8
9
10

---

(2)埃式筛（时间复杂度O（nloglongn））

注意：这里是判断从1到n每一个数是不是质数的时间复杂度，所以平均每一个时间复杂度应该是O(longn)

我们先用一个数组prime[]来储存每一个质数，用bool st[]来储存一个数是不是质数

**时间复杂度的分析：**没有打错，就是nloglogn,我们将每一个数的倍数全部标记为非质数（true）

/*
--------------------------
对于1到n的数：
2的倍数有2/n个
3的倍数有3/n个
...
n的倍数有n/n个
--------------------------
我们只需要全部加起来就是他的时间复杂度：
2/n+3/n+4/n+...+n/n=nlogn   (数学上的调和级数)
但是我们知道：1---n有n/logn个质数
那么结果是（n/logn）*（logn）=n
but-->实际上不是O（n）的时间复杂度，是O（nloglongn）
*/


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

具体的时间复杂度分析可以参考：通俗易懂的埃氏筛时间复杂度分析

下面给出板子：

const int N = 1e6+10;
int prime[N];
bool st[N];

//埃式筛
void get_primes(int n)
{
    int cnt=0;
    for(int i = 2;i <= n;i ++ )
    {
        if(!vis[i])
        {
            primes[cnt++]=i;
            for(int j = i*2;j <= n;j += i)
            vis[j]=true;
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

---

（3）线性筛（时间复杂度是真真正正的o(n)）

我们先来看代码，再来分析原理：

//线性筛
void get_primes(int n)
{
    int cnt = 0;
    for(int i = 2;i <= n;i ++ )
    {
        if(!vis[i]) primes[cnt++]=i;    
        for(int j = 0;primes[j] <= n/i;j ++ )
        {
            vis[primes[j]*i] = true;
            if(i%primes[j]==0) break;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

时间复杂度的分析：

为什么说时间复杂度是真真正正的O(n)呢？

是因为每一个数只被筛选了一次：

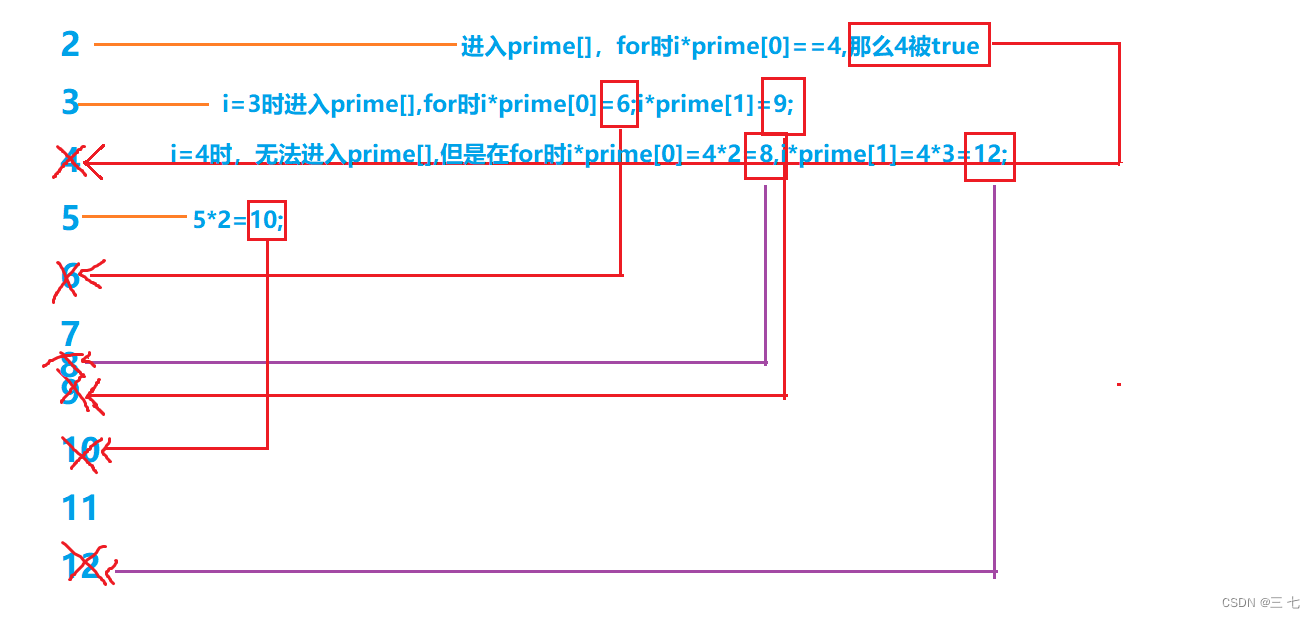
当然，严禁的证明也要给出来：

每一个数都可以写成质因子的乘积：

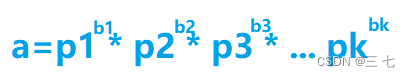
然后每一个数在他的前一个质因子里面会提前被筛（像上面的10被5*2筛去），也就是说一个数会被pi的数里面被筛一次

比如数字56，他的质因子为—>2 * 2 * 2 * 7,而不会表现为4 * 2 * 7或者4*14的形式，应该是28 * 2的形式

我们来看一下他的筛选过程：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e8+10;
int primes[N];
bool vis[N];
//线性筛
void get_primes(int n)
{
    int cnt = 0;
    for(int i = 2;i <= n;i ++ ){
        if(!vis[i]) primes[cnt++]=i;
        cout<<"第"<<i<<"次筛掉的数为："<<endl ;
        for(int j = 0;primes[j] <= n/i;j ++ ){
        	cout<< primes[j]*i <<" "<<"被"<<i<<"和"<<primes[j]<<"筛去"<<endl;
            vis[primes[j]*i] = true;
            if(i%primes[j]==0) break;
        }
        cout<<endl;
    }
    cout<<cnt<<endl;
}
int main()
{
    int n;
    cin >> n;
    get_primes(n);
    return 0; 
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

运行结果：

学是昨天学的，码是今天码的