Python 实现巴特沃斯滤波器_python butterworth滤波

1 巴特沃斯滤波设计步骤

①归一化处理。即令$\lambda =\omega /{\omega }_p$
②计算阶数，截止频率和通带频率比；
${\omega }_s$是阻带截止频率，${\omega }_p$是通带截止频率,${\delta }_s$是阻带应达到的最小衰减
${\lambda }_s={\omega }_s/{\omega }_p$
$N=\frac{\log \sqrt{(10^{({\delta }_s/10)}-1)}}{log{\lambda }_s}$
③构造归一化系统函数H§,其极点为$p_k=e^{(j(2k+N-1)\pi /2N)},k=1,2,3\dots K$,则有：
$$H(p)=\frac{1}{((p-p_1)(p-p_2)\dots .(p-p_N))}$$
④得到滤波器系统函数。
$$H(s)=H(p){|}_{(p=s⁄{\lambda }_s{\omega }_p)}$$

2 实例

3 python代码实现

由于笔算IIR滤波器参数较为复杂，本代码采用scipy中的butter滤波器直接计算出相应的参数，python实现IIR滤波算法较为简单，在该代码中被略去，有需要者，私聊博主。
感兴趣的读者可以对比计算得到的滤波器参数和教程中计算得到的参数，会发现其值与教材中计算的相差无几。

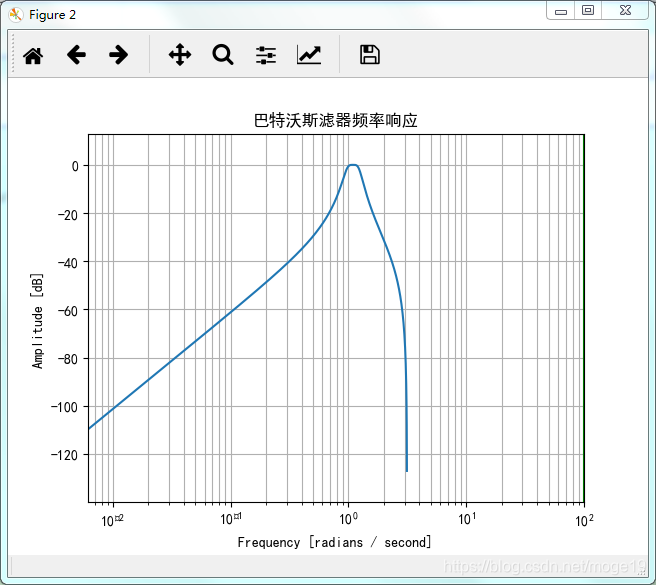
import numpy as np
import math
from sympy import *
from scipy import signal
import scipy 
import matplotlib
import matplotlib.pyplot as plt
from scipy.fftpack import fft,ifft
plt.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] =False

#设计一巴特沃斯带通滤波器
#通带下限频率150Hz
#通带上限频率200Hz
#下阻带下限频率100Hz
#上阻带下限频率250Hz
#通带衰减不大于3dB
#阻带衰减不小于18dB
#采样间隔T = 0.001s

fp_l = 150
fp_h = 200

fs_l = 100
fs_h = 250
T    = 0.001
fs   = int(1/T)

wp_l = 2*np.pi*fp_l * T
wp_h = 2*np.pi*fp_h * T
ws_l = 2*np.pi*fs_l * T
ws_h = 2*np.pi*fs_h * T

Wp_l = np.tan(wp_l/2)
Wp_h = np.tan(wp_h/2)
Ws_l = np.tan(ws_l/2)
Ws_h = np.tan(ws_h/2)

#计算中心频率
W_o = Wp_l*Wp_h
#计算通带带宽
W_BW = Wp_h-Wp_l

#对频率指标归一化
H_sl = Ws_l/W_BW
H_sh = Ws_h/W_BW

H_pl = Wp_l/W_BW
H_ph = Wp_h/W_BW

H_o  = H_pl*H_ph

#进行频率变换
L_p  = (H_ph**2 - H_o)/H_ph
L_sl = (H_sl**2 - H_o)/H_sl
L_sh = (H_sh**2 - H_o)/H_sh

if(abs(L_sh)<abs(L_sl)):
    L_s = L_sh
else:
    L_s = L_sl
#print(L_s)
#设计模拟低通滤波器
G_p = 3
G_s = 18
#确定滤波器阶数
N = math.log(np.sqrt(10**(G_s/10)-1),10)/math.log(L_s,10)
print(N)
#取大于N的数作为滤波阶数
#if(int(N)>N):
#    N=int(N)/2
#else:
#    N = (int(N)+1)/2
if(int(N)<N):
    N=int(N)+1
print(N)
fl = fp_l
fh = fp_h
Wn = [fl*2/fs,fh*2/fs]
x=np.linspace(0,1,fs)
#设置需要采样的信号
signal_array = np.sin(2*np.pi*500*x)
for i in range(10):
    if 100*i != 500:
        signal_array+=np.sin(2*np.pi*100*x*i)#+np.sin(2*np.pi*175*x)+np.sin(2*np.pi*350*x)+np.sin(2*np.pi*500*x)

noise_size = len(signal_array)
noise_array =  np.random.normal(0, 2, noise_size)
mu = 0
sigma = 0.12
import random
noise_array = random.gauss(mu,sigma)

adc_value=[]
test = []    
for i in range(noise_size):
    adc_value.append(random.gauss(mu,sigma))
    test.append(1)
#signal_array= np.array(adc_value) + np.array(test)
signal_size = len(signal_array)
K = np.arange(signal_size)
T1 = signal_size/fs
frequency_array = K/T1/10
#计算源信号的FFT
signal_fft=fft(signal_array)                     #快速傅里叶变换
signal_fft_abs=abs(fft(signal_array))                # 取模
signal_fft_abs_norm=abs(fft(signal_array))/((len(signal_array)/2))           #归一化处理
signal_fft_abs_norm_half= signal_fft_abs_norm[range(int(len(signal_array)/2))]  #由于对称性，只取一半区间
signal_fft_abs_size =np.arange(len(signal_array))        # 频率
IIR_filter=filter()

#计算巴特沃夫滤波器参数
b_weight,a_weight = scipy.signal.butter(N, Wn, btype='bandpass')
#利用计算得到的滤器参数进行滤波
IIR_Output =  IIR_filter.IIR_F(signal_array,a_weight,b_weight)
IIR_Output_Size = len(IIR_Output)

plt.figure(1)
plt.subplot(221)
plt.title('原始信号')  # 定义标题
plt.plot(signal_array[0:1000],'g') 
plt.subplot(222)
plt.title('滤波后的信号')  # 定义标题
#
#t=np.sin(2*np.pi*500*x)
#plt.plot(t[0:1000],'g') 
#plt.plot(signal_array[0:1000],'g') 
plt.plot(IIR_Output[0:1000],'b') 
plt.show()

IIR_Output = np.array(IIR_Output)
IIR_Output_fft=fft(IIR_Output)                     #快速傅里叶变换
IIR_Output_fft_abs=abs(fft(IIR_Output))                # 取模
IIR_Output_fft_abs_norm=abs(fft(IIR_Output))/((len(IIR_Output)/2))           #归一化处理
IIR_Output_fft_abs_half = IIR_Output_fft_abs_norm[range(int(len(IIR_Output)/2))]  #由于对称性，只取一半区间
IIR_Output_fft_abs_size = np.arange(len(IIR_Output_fft_abs_norm))        # 频率
plt.subplot(223)
plt.title('原始信号FFT')  # 定义标题
plt.plot(signal_fft_abs_size[0:1000],signal_fft_abs_norm[0:1000],'g') #显示原始信号的FFT模值
plt.subplot(224)
plt.title('滤波后的信号FFT')  # 定义标题
plt.plot(signal_fft_abs_size[0:1000],IIR_Output_fft_abs_norm[0:1000],'r',label='FFT') 
#plt.legend('滤波后信号FFT')
plt.show()
plt.figure(2)

w, h = signal.freqz(b_weight, a_weight)
plt.semilogx(w, 20 * np.log10(abs(h)),markersize = 15)
plt.title('巴特沃斯滤器频率响应')
plt.xlabel('Frequency [radians / second]')
plt.ylabel('Amplitude [dB]')
plt.margins(0, 0.1)
plt.grid(which='both', axis='both')
plt.axvline(100, color='green') # cutoff frequency
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155

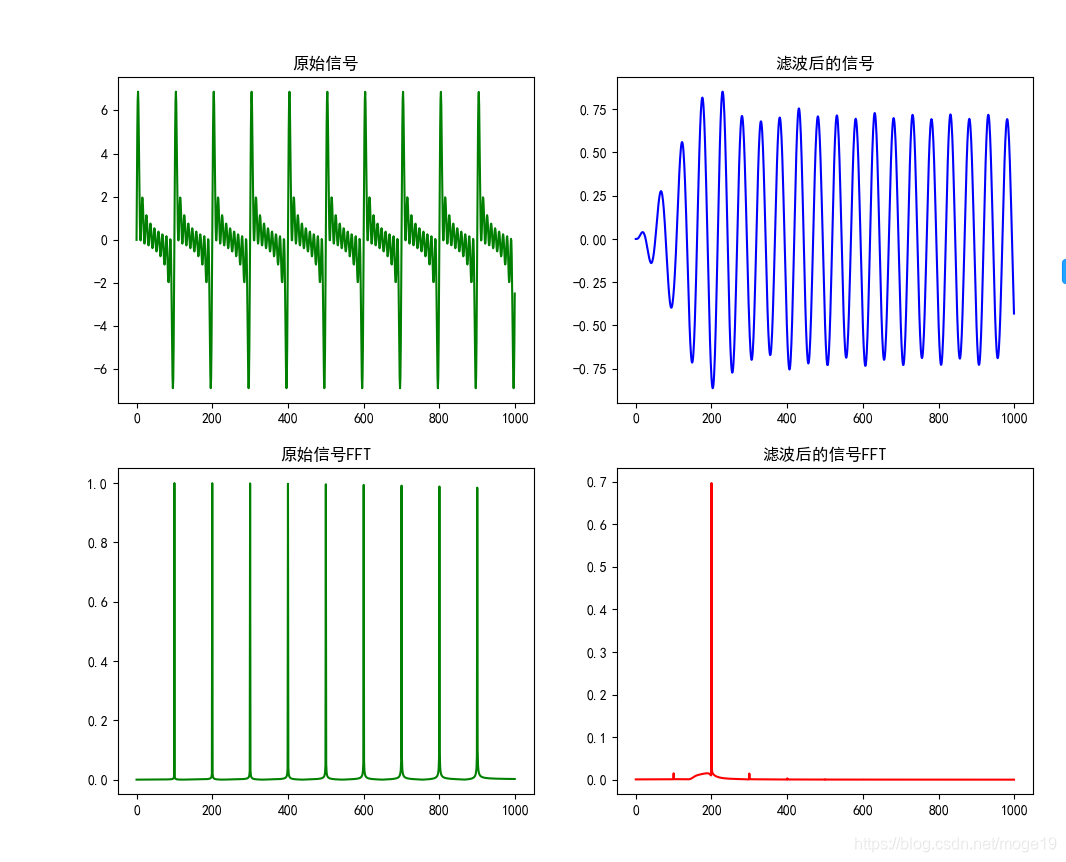
4 运行结果

通过对比下图，可见滤波后的频谱图显示无关频道的信号得到有效衰减，但是滤波后的信号，仍然没有得到较好的信号信息，这里可以采用零相移滤波器来实现可得到更好的滤波效果。


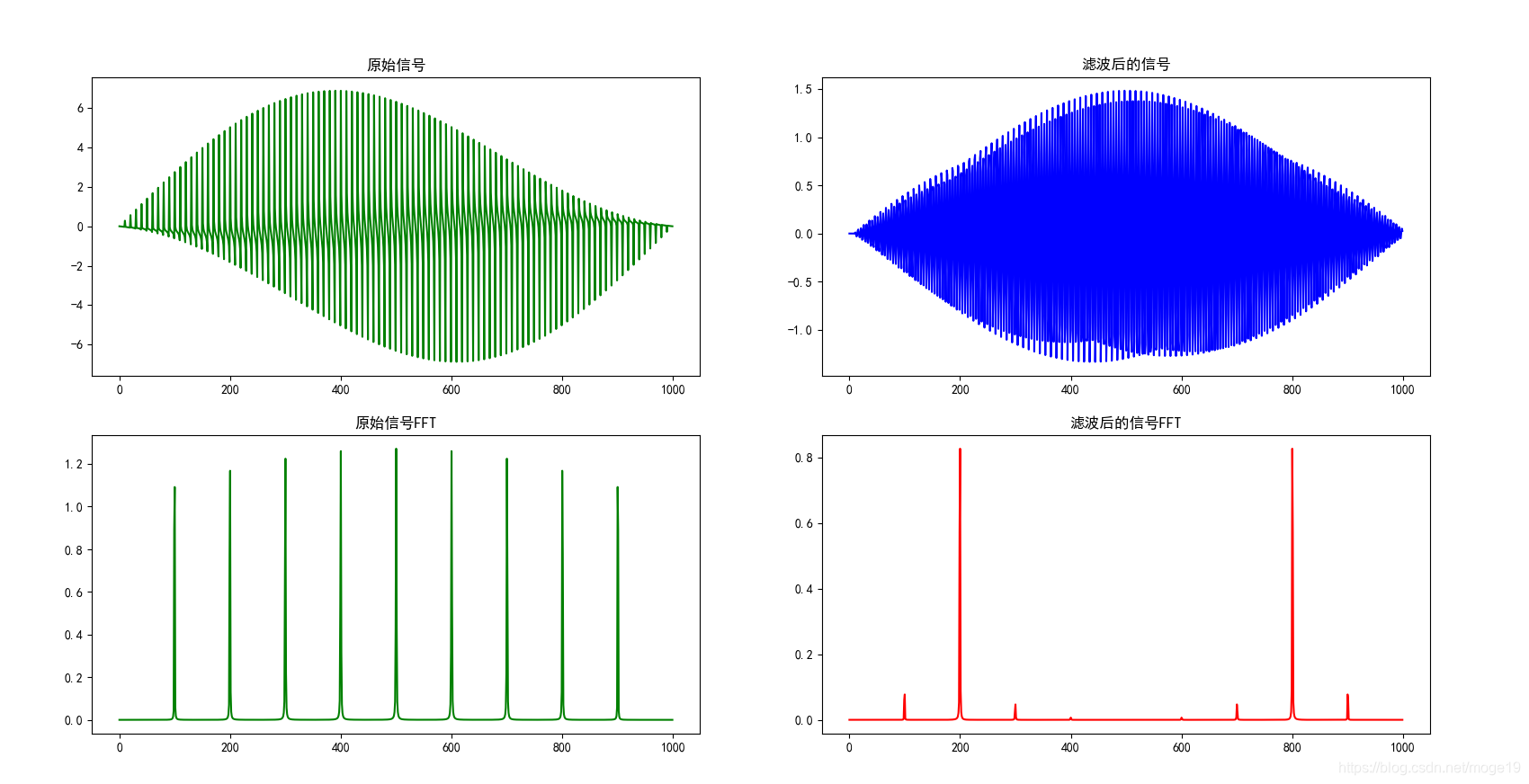
可见滤波效果并不是特别好，若提高采样频率，将T=0.0001,得到如下结果：