生成式对抗网络GAN研究进展（二）——原始GAN_collapse problem

【前言】
    本文首先介绍生成式模型，然后着重梳理生成式模型（Generative Models）中生成对抗网络（Generative Adversarial Network）的研究与发展。作者按照GAN主干论文、GAN应用性论文、GAN相关论文分类整理了45篇近两年的论文，着重梳理了主干论文之间的联系与区别，揭示生成式对抗网络的研究脉络。
涉及的论文有：
[1] Goodfellow Ian, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[C]//Advances in Neural Information Processing Systems. 2014: 2672-2680.
[2] Mirza M, Osindero S. Conditional Generative Adversarial Nets[J]. Computer Science, 2014:2672-2680.
[3] Denton E L, Chintala S, Fergus R. Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks[C]//Advances in neural information processing systems. 2015: 1486-1494.
[4] Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks[J]. arXiv preprint arXiv:1511.06434, 2015.
[5] Im D J, Kim C D, Jiang H, et al. Generating images with recurrent adversarial networks[J]. arXiv preprint arXiv:1602.05110, 2016.
[6] Larsen A B L, Sønderby S K, Winther O. Autoencoding beyond pixels using a learned similarity metric[J]. arXiv preprint arXiv:1512.09300, 2015.
[7] Wang X, Gupta A. Generative Image Modeling using Style and Structure Adversarial Networks[J]. arXiv preprint arXiv:1603.05631, 2016.
[8] Chen X, Duan Y, Houthooft R, et al. InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets[J]. arXiv preprint arXiv:1606.03657, 2016.
[9] Kurakin A, Goodfellow I, Bengio S. Adversarial examples in the physical world[J]. arXiv preprint arXiv:1607.02533, 2016.
[10] Odena A. Semi-Supervised Learning with Generative Adversarial Networks[J]. arXiv preprint arXiv:1606.01583, 2016.
[11] Springenberg J T. Unsupervised and Semi-supervised Learning with Categorical Generative Adversarial Networks[J]. arXiv preprint arXiv:1511.06390, 2015.

2. 生成式对抗网络，Generative Adversarial Networks

2.1 GAN的思想与训练方法

    GAN[Goodfellow Ian，GAN]启发自博弈论中的二人零和博弈（two-player game），由[Goodfellow et al, NIPS 2014]开创性地提出。在二人零和博弈中，两位博弈方的利益之和为零或一个常数，即一方有所得，另一方必有所失。GAN模型中的两位博弈方分别由生成式模型（generative model）和判别式模型（discriminative model）充当。生成模型G捕捉样本数据的分布，判别模型是一个二分类器，估计一个样本来自于训练数据（而非生成数据）的概率。G和D一般都是非线性映射函数，例如多层感知机、卷积神经网络等。如图2-1所示，左图是一个判别式模型，当输入训练数据x时，期待输出高概率（接近1）；右图下半部分是生成模型，输入是一些服从某一简单分布（例如高斯分布）的随机噪声z，输出是与训练图像相同尺寸的生成图像。向判别模型D输入生成样本，对于D来说期望输出低概率（判断为生成样本），对于生成模型G来说要尽量欺骗D，使判别模型输出高概率（误判为真实样本），从而形成竞争与对抗。
                

    GAN模型没有损失函数，优化过程是一个“二元极小极大博弈（minimax two-player game）”问题:
                
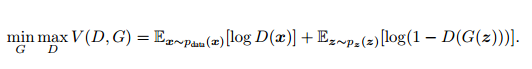
    这是关于判别网络D和生成网络G的价值函数（Value Function），训练网络D使得最大概率地分对训练样本的标签（最大化log D(x)），训练网络G最小化log(1 – D(G(z)))，即最大化D的损失。训练过程中固定一方，更新另一个网络的参数，交替迭代，使得对方的错误最大化，最终，G 能估测出样本数据的分布。生成模型G隐式地定义了一个概率分布Pg，我们希望Pg 收敛到数据真实分布Pdata。论文证明了这个极小化极大博弈当且仅当Pg = Pdata时存在最优解，即达到纳什均衡，此时生成模型G恢复了训练数据的分布，判别模型D的准确率等于50%。
                
                                                      图2-2 生成式对抗网络算法流程

2.2 GAN的优势与缺陷

    与其他生成式模型相比较，生成式对抗网络有以下四个优势【OpenAI Ian Goodfellow的Quora问答】：

• 根据实际的结果，它们看上去可以比其它模型产生了更好的样本（图像更锐利、清晰）。
• 生成对抗式网络框架能训练任何一种生成器网络（理论上-实践中，用 REINFORCE 来训练带有离散输出的生成网络非常困难）。大部分其他的框架需要该生成器网络有一些特定的函数形式，比如输出层是高斯的。重要的是所有其他的框架需要生成器网络遍布非零质量（non-zero mass）。生成对抗式网络能学习可以仅在与数据接近的细流形（thin manifold）上生成点。
• 不需要设计遵循任何种类的因式分解的模型，任何生成器网络和任何鉴别器都会有用。
• 无需利用马尔科夫链反复采样，无需在学习过程中进行推断（Inference），回避了近似计算棘手的概率的难题。

    与PixelRNN相比，生成一个样本的运行时间更小。GAN 每次能产生一个样本，而 PixelRNN 需要一次产生一个像素来生成样本。
    与VAE 相比，它没有变化的下限。如果鉴别器网络能完美适合，那么这个生成器网络会完美地恢复训练分布。换句话说，各种对抗式生成网络会渐进一致（asymptotically consistent），而 VAE 有一定偏置。
与深度玻尔兹曼机相比，既没有一个变化的下限，也没有棘手的分区函数。它的样本可以一次性生成，而不是通过反复应用马尔可夫链运算器（Markov chain operator）。
与 GSN 相比，它的样本可以一次生成，而不是通过反复应用马尔可夫链运算器。
与NICE 和 Real NVE 相比，在 latent code 的大小上没有限制。

GAN目前存在的主要问题：

• 解决不收敛（non-convergence）的问题。
      目前面临的基本问题是：所有的理论都认为 GAN 应该在纳什均衡（Nash equilibrium）上有卓越的表现，但梯度下降只有在凸函数的情况下才能保证实现纳什均衡。当博弈双方都由神经网络表示时，在没有实际达到均衡的情况下，让它们永远保持对自己策略的调整是可能的【OpenAI Ian Goodfellow的Quora】。
• 难以训练：崩溃问题（collapse problem）
      GAN模型被定义为极小极大问题，没有损失函数，在训练过程中很难区分是否正在取得进展。GAN的学习过程可能发生崩溃问题（collapse problem），生成器开始退化，总是生成同样的样本点，无法继续学习。当生成模型崩溃时，判别模型也会对相似的样本点指向相似的方向，训练无法继续。【Improved Techniques for Training GANs】
• 无需预先建模，模型过于自由不可控。
      与其他生成式模型相比，GAN这种竞争的方式不再要求一个假设的数据分布，即不需要formulate p(x)，而是使用一种分布直接进行采样sampling，从而真正达到理论上可以完全逼近真实数据，这也是GAN最大的优势。然而，这种不需要预先建模的方法缺点是太过自由了，对于较大的图片，较多的 pixel的情形，基于简单 GAN 的方式就不太可控了。在GAN[Goodfellow Ian, Pouget-Abadie J] 中，每次学习参数的更新过程，被设为D更新k回，G才更新1回，也是出于类似的考虑。

Reference

[1] Goodfellow Ian, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[C]//Advances in Neural Information Processing Systems. 2014: 2672-2680.
[2] 深度 | OpenAI Ian Goodfellow的Quora问答：高歌猛进的机器学习人生. 作者：Ian Goodfellow. 机器之心编译
[3] Barone A V M. Towards cross-lingual distributed representations without parallel text trained with adversarial autoencoders[J]. arXiv preprint arXiv:1608.02996, 2016.