Cpp五条

这个屌丝很懒，什么也没留下！

热门标签

（Java实习生）每日10道面试题打卡——Java简单集合篇_java实习生集合面试题大全

作者：Cpp五条 | 2024-03-12 23:55:37

踩

java实习生集合面试题大全

临近秋招，备战暑期实习，祝大家每天进步亿点点！
本篇总结的是Java集合知识相关的面试题，后续会每日更新~

在这里插入图片描述

1、请问如何使ArrayList保证线程安全？

答案如下：

// 方式一：
// synchronizedList底层相当于把集合的set add remove方法加上synchronized锁
List<Object> list = Collections.synchronizedList(new ArrayList<>());

// 方式二：
// 使用线程安全的CopyOnWriteArrayList,其底层也是对增删改方法进行加锁：final ReentrantLock lock = this.lock;

// 方式三：
// 自己写一个包装类，继承ArrayList 根据业务，对add set remove方法进行加锁控制
1
2
3
4
5
6
7
8
9

2、说一说Vector 和 ArrayList 的区别？

二者初始容量均为 0，即在调用空参构造函数实例化时，二者容量为 0，并在第一次加入元素数据时附上初始容量值 10。
Vector 扩容时，如果未指定扩容递增值capacityIncrement，或该值不大于 0 时，每次扩容为原来的 2 倍，否则扩容量为capacityIncrement的值。
ArrayList 扩容时，每次扩容为原来的 1.5 倍。
Vector是线程安全集合，通过对remove、add等方法加上synchronized关键字来实现。ArrayList 是非线程安全集合。

参考文章：JDK集合源码之ArrayList解析(附带面试题举例)、JDK集合源码之Vector解析

3、请问CopyOnWriteArrayList添加新元素是否需要扩容？具体是如何做的？

CopyOnWriteArrayList 底层并非动态扩容数组，不能动态扩容，其线程安全是通过加可重入锁 ReentrantLock 来保证的。
当向 CopyOnWriteArrayList 添加元素时，线程获取锁的执行权后，add 方法中会新建一个容量为（旧数组容量+1）的数组，将旧数组数据拷贝到该数组中，并将新加入的数据放入新数组尾部。

代码如下：

public boolean add(E e) {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        Object[] elements = getArray();
        int len = elements.length;
        Object[] newElements = Arrays.copyOf(elements, len + 1);
        newElements[len] = e;
        setArray(newElements);
        return true;
    } finally {
        lock.unlock();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

CopyOnWriteArrayList 适用于，读多写少的情况下（读写分离）！因为每次调用修改数组结构的方法都需要重新新建数组，性能低！

文章参考：JDK集合源码之CopyOnWriteArrayList解析

4、HashMap 与 HashTable 的区别？

HashMap：

HashMap：底层是基于数组+链表 + 红黑树，非线程安全的，默认容量是16、允许有空的健和值。
初始size为16，扩容：newsize = oldsize << 1，size一定为2的n次幂。
当Map中元素总数超过Entry数组的75%，触发扩容操作，为了减少链表长度，元素分配更均匀计算index方法：index = hash & (tab.length – 1)。
扩容针对整个Map，每次扩容时，原来数组中的元素依次重新计算存放位置，并重新插入。

HashTable：

HashTable：底层数组+链表实现，无论key还是value都不能为null，线程安全，实现线程安全的方式是在修改数据时锁(synchroized)住整个HashTable，效率低，ConcurrentHashMap做了相关优化。
初始size为11，扩容：(tab.length << 1) + 1。
计算index的方法：index = (hash & 0x7FFFFFFF) % tab.length。

二者区别：

HashMap不是线程安全的，HashTable是线程安全的(使用 synchronized 修饰)。
HashMap允许将null作为一个entry的key或者value，而Hashtable不允许。

HashMap 的 hash 值重新计算过(如下面的代码)，Hashtable 直接使用 hashCode。

// HashMap中重新计算hash值的算法
static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
1
2
3
4
5

Hashtable继承自Dictionary类，而HashMap是Map 接口的一个实现类。

HashMap与HashTable 求桶位index的寻址算法：

HashMap：index = hash & (tab.length – 1)
HashTable：index = (hash & 0x7FFFFFFF) % tab.length

二者求桶位index的公式都是为了使每次计算得到的桶位index更分散，这样可以降低哈希冲突。

HashTable中：

0x7FFFFFFF 是0111 1111 1111 1111 1111 1111 1111 1111：除符号位外的所有 1。
(hash & 0x7FFFFFFF)得到的结果将产生正整数。
(hash & 0x7FFFFFFF) % tab.length 计算得到的index结果始终为正整数，且确保index的值在 tab.length 范围内！
HashTable 的数组长度采用奇数导致的hash冲突会比较少，采用偶数会导致的冲突会增多！所以初始容量为 11，扩容为newsize = olesize << 1+1（即 2n + 1 倍），保证每次扩容结果均为奇数。

HashMap中：

初始容量为 16，当有效数据数量达到数组容量的 0.75 倍时，触发扩容。
桶位计算公式：index = hash & (tab.length – 1)，计算桶位index时，容量一定要为 2 的 n 次幂（即偶数），这样是为了减少 hash 冲突，扩容：newsize = oldsize << 1（即 2n 倍），得到的结果也是偶数。
此外桶中的链表长度大于 8 时且数组长度达到 64，链表进行树化，小于 6 时进行反树化。
JDK1.8前HashMap中的链表采用的是头插法，优点是：效率高于尾插法，因为不需要遍历一次链表再进行数据插入。
JDK1.8后使用尾插法，之所以采用尾插法是因为要去判段链表的长度是否大于了 8，这种情况要考虑树化。
HashMap解决哈希冲突的方法采用的是：链表法。
HashMap是先插入数据再判断是否需要库容！

文章参考：JDK集合源码之HashMap解析(上)、JDK集合源码之HashMap解析(下)、JDK集合源码之HashTable解析

5、HashMap和TreeMap的区别？

HashMap 上面介绍过了，直接看TreeMap。
TreeMap 底层是基于平衡二叉树(红黑树)，可以自定义排序规则，要实现 Comparator 接口，能便捷的实现内部元素的各种排序 TreeMap(Comparetor c)，但是性能比 HashMap 差。

6、Set和Map的关系

二者核心都是不保存重复的元素，存储一组唯一的对象。
Set 的每一种实现都是对应 Map里面的一种封装。
例如HashSet 底层对应的就是封装了HashMap，TreeSet底层就是封装了TreeMap。

7、HashMap底层为什么选择红黑树而不用其他树，比如二叉查找树，为什么不一开始就使用红黑树，而是链表长度到达8且数组容量大于64的时候才树化？

二叉查找树在特殊情况下也会变成一条线性结构，和原先的长链表存在一样的深度遍历问题，查找性能慢，例如：
使用红黑树主要是为了提升查找数据的速度，红黑树是平衡二叉树的一种，插入新数据（新数据初始是红色结点插入）后会通过左旋，右旋，变色等操作来保持平衡，解决单链表查询深度的问题。
之所以一开始不用红黑树是因为，当链表数据量少的时候，遍历线性链表比遍历红黑树消耗的资源少 (因为少量数据，红黑树本身自选、变色保持平衡也是需要消耗资源的)，所以前期使用线性表。
而之所以以 8 为树化门槛，是因为经过大量测试，8 这个值是最合适的。理想情况下，使用随机的哈希码，节点分布在 hash 桶中的频率遵循泊松分布，按照泊松分布的公式计算，链表中节点个数为 8 时的概率为 0.00000006，这个概率足够低了，并且到 8 个节点时，红黑树的性能优势也会开始展现出来，因此 8 是一个较合理的数字。

既然提到了红黑树，也必然会问红黑树的5个性质：

红黑树的性质
性质1：每个节点要么是黑色，要么是红色。
性质2：根节点是黑色。
性质3：每个叶子节点（NIL）是黑色。
性质4：每个红色节点的两个子节点一定都是黑色。不能有两个红色节点相连。
性质5：任意一节点到每个叶子节点的路径都包含数量相同的黑结点。俗称：黑高！

红黑树实例图:

在这里插入图片描述

红黑树并不是一个完美平衡二叉查找树，从图上可以看到，根结点P的左子树显然比右子树高，

但左子树和右子树的黑结点的层数是相等的，也就是说，任意一个结点到到每个叶子结点的路径都包含数量相同的黑结点(性质5)。

所以我们叫红黑树这种平衡为黑色完美平衡。

那么当某个桶位发生 hash 冲突时，不直接使用红黑树，而是先使用链表呢？

首先，我们要知道，链表不是数组，它的存储地址并不是连续的，当检索数据时，需要通过指针逐一 next ，直到找到目标数据。
如果桶中 hash 冲突次数较少，那么遍历链表耗费的时间并不多。但是，一旦 hash 冲突次数比较多，导致桶位中形成的链表长度很长，那么遍历一次长链表花费的时间就需要很多！
而如果将长链表树化成一颗红黑树，红黑树是一种特殊的二叉树，二叉树是可以对半查找的，理想情况下可以直接将查询耗时折半！
之所以一开始不直接使用红黑树，因为毕竟树结构占用的存储空间肯定是要比链表大很多的，因此当链表长度较短时，没必要树化！

总之，链表和红黑树的取舍完全是出于对时间效率和空间大小的一种权衡把~

参考文章：HashMap底层红黑树实现(自己实现一个简单的红黑树)

8、为什么 HashMap 容量必须是 2 的 N 次幂？如果输入值不是 2 的幂比如 10 会怎么样?

问题一：为什么 HashMap 容量必须是 2 的 N 次幂？

核心目的是为了使插入的结点均匀分布，减少 hash 冲突。

HashMap 构造方法可以指定集合的初始化容量大小，如：

// 构造一个带指定初始容量和默认负载因子（0.75)的空 HashMap。
HashMap(int initialCapacity)
1
2

当向 HashMap 中添加一个元素的时候，需要根据 key 的 hash 值，去确定其在数组中的具体桶位(寻址算法)。HashMap 为了存取高效，减少碰撞，就是要==尽量把数据分配均匀，每个链表长度大致相同==，这个实现的关键就在把数据存到哪个链表中的算法。

这个算法实际就是取模运算：hash % tab.length，而计算机中直接求余运算效率不如位移运算。所以源码中做了优化，使用 hash & (tab.length- 1)来寻找桶位。而实际上 hash % length 等于 hash & ( length - 1) 的前提是 length 必须为 2 的 n 次幂。

例如，数组长度 tab.length = 8 的时候，3 & (8 - 1) = 3，2 & (8 - 1) = 2，桶的位置是(数组索引) 3 和 2，不同位置上，不发生 hash 碰撞。

再来看一个数组长度(桶位数)不是 2 的 n 次幂的情况：

从上图可以看出，当数组长度为 9 (非 2 的 n 次幂)的时候，不同的哈希值 hash， hash & (length - 1)所得到的数组下标相等(很容易出现哈希碰撞)。

那么我们来总结一下 HashMap 数组容量使用 2 的 n 次幂的原因：

① 当根据 key 的 hash 值寻址计算确定桶位下标 index 时，如果HashMap 的数组长度 tab.length 是 2 的 n 次幂数，那么就可以保证新插入数组中的数据均匀分布，每个桶位都有可能分配到数据，而如果数组长度不是 2 的 n 次幂数，那么就可能导致一些桶位上永远不会被插入到数据，反而有些桶位频繁发生 hash 冲突，导致数组空间浪费，冲hash 突概率增加。
② 一般我们人的逻辑寻找数组桶位下标 index ，往往会采用取模运算的方式来确定 index，即 index = hash % length，然而计算机进行取模预算的效率远不如位运算，因此需要被改进成 hash & (length - 1)的方式寻址。本质上，两种方式计算得到的结果是相同的，即：hash & (length - 1) = hash % length。

因此，HashMap 数组容量使用 2 的 n 次幂的原因，就是为了使新插入的数据在寻址算法确定桶位下标时，尽量保证新数据能均匀的分布在每个桶位上，尽量降低某个桶位上频繁发生 hash 冲突的概率。毕竟某个桶位中的 hash 冲突次数越多，桶内的链表长度越长，这样导致数据检索的时候效率大大降低 (因为数组线性查询肯定要比链表快很多)。

问题二：如果创建HashMap对象时，输入的数组长度length是10，而不是2的n次幂会怎么样呢？

例如：

HashMap<String, Integer> hashMap = new HashMap(10);
1

这种情况下，HashMap双参构造函数会通过 tableSizeFor(initialCapacity)方法，得到一个最接近length且大于length的 2 的 n 次幂数(比如最接近 10 且大于 10 的 2 的 n 次幂数是 16 )

大于等于该容量的最小的 2 的 N 次方数的计算方法如下：

static final int tableSizeFor(int cap) {
    int n = cap - 1;
    n |= n >>> 1;
    n |= n >>> 2;
    n |= n >>> 4;
    n |= n >>> 8;
    n |= n >>> 16;
    return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
1
2
3
4
5
6
7
8
9

这个方法tableSizeFor(initialCapacity);就是用于获得大于等于 initialCapacity 的最小的 2 的 n 次幂数。

这里设计到位运算，由于是面试题，就不再一步步讲解如何运算递推了，直接附上一个案例图，详细地推请参考下面的源码分析文章：

文章参考：JDK集合源码分析——HashMap(上)

9、HashMap计算 key 的 hash 值，是怎么设计的？为什么要将 hashCode 的高16位参与运算？

HashMap中重新计算 hash 值的方法如下：

static final int hash(Object key) {
    int h;
    // 如果key为null，则hash值为0,
    // 否则调用key的hashCode()方法计算出key的哈希值然后赋值给h,
    // 然后与 h无符号右移16位后的二进制数进行按位异或 得到最终的hash值,
    // 这样做是为了使计算出的hash更分散,
    // 为什么要更分散呢？因为越分散，某个桶的链表长度就越短，之后生成的红黑树越少，检索效率越高！
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
1
2
3
4
5
6
7
8
9

如上代码所示：将 key 的 hashCode 的高 16 位和 hashCode 低 16 位进行异或（XOR）运算，最终得到新的 hash 值。

该方法分析如下：

key.hashCode()；返回散列值也就是 hashcode，假设随便生成的一个值。
^（按位异或运算）运算规则：相同的二进制数位上，数字相同，结果为 0，不同为 1。
h >>> 16 将 h 的值进行无符号右移 16 位。

问题：为什么要这样操作呢？

我们知道，HashMap 新插入的数据需要经过寻址算法 index = hash & (tab.length - 1)来确定桶位下标。tab.length就是数组长度，我们这里设其为 n。

如果当 n 即数组长度很小，假设是 n = 16 的话，那么 n - 1 是 15 ，其二进制数为 1111 ，这样的值和 hashCode 直接做按位与操作，实际上只使用了哈希值的后 4 位。如果当哈希值的高位变化很大，低位变化很小，这样就很容易造成哈希冲突了，所以这里把高低位都利用起来，从而解决了这个问题。

我们来看一个分析图：

由上图，可以知道如果只使用 key.hashCode()方法计算得到的 hash 值，那么当 hash 值高位变化较大，而低位变化较小时，通过寻址算法 hash & (tab.length - 1) 得到的桶位下标 index 就更容易出现 hash 冲突了！

10、说一说你对hash算法的理解？以及什么是hash 冲突？

hash 的基本概念就是把任意长度的输入，通过 hash 算法之后，映射成固定长度的输出。
在程序中可能会碰到两个 value 值经过 hash 算法计算之后，算出了同样的 hash 值，这种情况就叫做 hash 冲突。

最后，再给大家推荐一个更硬核的HashMap分析点：为什么负载因子要设置为 0.75 ?

参考文章：华为面试官：为什么HashMap的加载因子是0.75？

补充题：说一说 resize 扩容时，旧数组元素向新数组中迁移的方式？

HashMap 进行扩容时，会伴随着一次重新 hash 分配，并且会遍历旧数组中所有的元素，并将其迁移到扩容后的新数组中。旧数组中的数据迁移有三种情况，下面分别来分析一下：

情况一、当前桶位中没有发生 hash 冲突，只有一个元素：

这种情况下，HashMap 使用的 rehash 方式非常巧妙，因为每次扩容都是翻倍，与原来计算的 (n - 1) & hash 的结果相比，只是多了一个 bit 位，所以结点要么就在原来的位置，要么就被分配到 “原位置 + 旧容量” 这个位置。

例如我们从 16 扩展为 32 时，具体的变化如下所示：

由于元素在重新计算 hash 之后，数组长度 n 变为原来的 2 倍，那么 n - 1 的标记范围在高位多 1bit(红色标记)，因此新的 index 就会发生这样的变化。

说明：

上图中 5 是假设计算出来的原来的索引。这样就验证了上述所描述的：扩容之后所以结点要么就在原来的位置，要么就被分配到 “原位置 + 旧容量” 这个位置。

因此，我们在扩充 HashMap 的时候，不需要重新计算 hash，只需要看看原来的 hash 值新增的那个 bit 是 1 还是 0 就可以了，是 0 的话索引没变，是 1 的话索引变成 “原位置 + 旧容量” 。可以看看下图为 16 扩充为 32 的 resize 示意图：

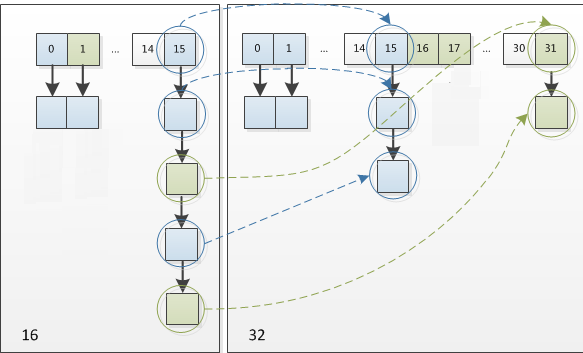
正是因为这样巧妙的 rehash 方式，既省去了重新计算 hash 值的时间，而且同时，由于新增的 1bit 是 0 还是 1 可以认为是随机的，在 resize 的扩容过程中保证了 rehash 之后每个桶上的结点数一定小于等于原来桶上的结点数，保证了 rehash 之后不会出现更严重的 hash 冲突，均匀的把之前的冲突的结点分散到新的桶中了。

情况二、当前桶位中发生了 hash 冲突，并且形成链表，但不是红黑树：

这时候，将桶中的链表拆分成 高位链 和 低位链 两个链表依次放入扩容后的新数组中。文字描述不如直接上代码：

	// 说明：hashMap本次扩容之前，table不为null
    if (oldTab != null) {
        // 把每个bucket桶的数据都移动到新的散列表中
        // 遍历旧的哈希表的每个桶，重新计算桶里元素的新位置
        for (int j = 0; j < oldCap; ++j) {
            // 当前node节点
            Node<K,V> e;
            // 说明：此时的当前桶位中有数据，但是数据具体是 
            // 1.单个数据 、 2.还是链表 、 3.还是红黑树 并不能确定
            if ((e = oldTab[j]) != null) {
                // 原来的数据赋值为null 便于GC回收
                oldTab[j] = null;
                // 第一种情况：判断数组是否有下一个引用(是否是单个数据)
                if (e.next == null)
                    // 没有下一个引用，说明不是链表，
                    // 当前桶上只有单个数据的键值对，
                    // 可以将数据直接放入新的散列表中
                    // e.hash & (newCap - 1) 寻址公式得到的索引结果有两种：
                    // 1.和原来旧散列表中的索引位置相同，
                    // 2.原来旧散列表中的索引位置i + 旧容量oldCap
                    newTab[e.hash & (newCap - 1)] = e;
                // 第二种情况：桶位已经形成红黑树
                else if (e instanceof TreeNode)
                    // 说明是红黑树来处理冲突的，则调用相关方法把树分开
                    // 红黑树这块，我会单独写一篇博客给大家详细分析一下
                    // 红黑树相关可以先跳过
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                // 第三种情况：桶位已经形成链表
                else { // 采用链表处理冲突
                    // 低位链表：
                    // 扩容之后数组的下标位置，与当前数组的下标位置一致 时使用
                    Node<K,V> loHead = null, loTail = null;
                    // 高位链表：扩容之后数组的下标位置等于
                    // 当前数组下标位置 + 扩容之前数组的长度oldCap 时使用
                    Node<K,V> hiHead = null, hiTail = null;
                    Node<K,V> next;
                    
                    // 通过上述讲解的原理来计算结点的新位置
                    do {
                        // 原索引
                        next = e.next;
                     	// 这里来判断如果等于true 
                        // e这个结点在resize之后不需要移动位置
                        // 举例：
                        // 假如hash1     -> ...... 0 1111
                        // 假如oldCap=16 -> ...... 1 0000
                        // e.hash & oldCap 结果为0，则
                        // 扩容之后数组的下标位置j，与当前数组的下标位置一致
                        // 使用低位链表
                        if ((e.hash & oldCap) == 0) {
                            if (loTail == null)
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        }
                        // 举例：
                        // 假如hash2     -> ...... 1 1111
                        // 假如oldCap=16 -> ...... 1 0000
                        // e.hash & oldCap 结果不为0，则
                        // 扩容之后数组的下标位置为：
                        // 当前数组下标位置j + 扩容之前数组的长度oldCap
                        // 使用高位链表
                        else {
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                    
                    // 将低位链表放到bucket桶里
                    if (loTail != null) {
                        loTail.next = null;
                        // 索引位置=当前数组下标位置j
                        newTab[j] = loHead;
                    }
                    // 将高位链表放到bucket里
                    if (hiTail != null) {
                        hiTail.next = null;
                        // 索引位置=当前数组下标位置j + 扩容之前数组的长度oldCap
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88