2023第十四届蓝桥杯JavaA组真题 试题D:棋盘_2023蓝桥杯java竞赛a组

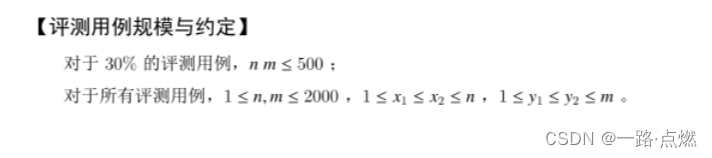
 试题D如果用暴力思路是O(n^3)的时间复杂度，只能过30%的测试点。

将x1,y1,x2,y2范围内的棋子颜色取反，可以考虑用差分操作实现O(1)的时间复杂度，暴力是O(n^2)的时间复杂度。

由于棋子只有两种颜色，且初始均为白色。因此，我们可以定义一个二维前缀和数组

pre[i][j]表示i,j格上的棋子颜色改变的次数。如果为偶数次，则最终颜色未发生改变，仍为白色；如果为奇数次，则最终颜色发生改变，变为黑色。

代码如下：

import java.util.*;
public class Main{
    public static void main(String[] args) {
        Scanner in=new Scanner(System.in);
        int n=in.nextInt();
        int m=in.nextInt();
        int[][] dif=new int[n][n];
        int[][] pre=new int[n][n];
        while(m-->0){
            //注意输入下标为1~n,数组下标为0~n-1,所以要-1
            int x1=in.nextInt()-1;
            int y1=in.nextInt()-1;
            int x2=in.nextInt()-1;
            int y2=in.nextInt()-1;
            
            dif[x1][y1]++;
            if(x2+1<n) dif[x2+1][y1]--;
            if(y2+1<n) dif[x1][y2+1]--;
            if(x2+1<n&&y2+1<n)  dif[x2+1][y2+1]++;
        }
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                int sum1=0,sum2=0,sum3=0;
                if(i-1>=0)  sum1=pre[i-1][j];
                if(j-1>=0)  sum2=pre[i][j-1];
                if(i-1>=0&&j-1>=0)  sum3=pre[i-1][j-1];
                pre[i][j]=sum1+sum2-sum3+dif[i][j];
                
                if((pre[i][j]%2)==0){
                    System.out.print(0);
                }else{
                    System.out.print(1);
                }
            }
            System.out.println();
        }
 
    }
}

 每次修改操作的时间复杂度为O(1)

最终的时间复杂度为O(n^2)