- 1谈谈程序员面试之刷题
- 2深度解析MBTI:了解其发展历史与演变过程(包含开源免费的API接口)
- 3自定义表单元素组件内容变化触发ElForm重新校验
- 4阿里巴巴一面 :十道经典面试题解析_阿里面试题
- 5聊天机器人是人工智能吗?探索人机交互的未来
- 6Stable Diffusion 秋叶整合包v4.7 :解压即用,快速入门AI绘画_stable diffusion秋叶整合包
- 7FPGA认识-什么是FPGA(1)_fpga是什么
- 8美赛、国赛数模竞赛最后一层遮羞布——查重问题_美赛被判dq会公示嘛
- 9想进BAT的 iOS程序员,看完这个你还觉得Offer难拿吗?_非程序员进bat难吗
- 10霸榜GitHub Top 500的中国开源项目
复杂网络建模(一)
赞
踩
度、平均度以及度分布
节点的度就是该节点的邻边数量。平均度就是所有节点度的平均值。度分布描述了节点度的分布情况,通常用直方图来表示。
连通性
无向网络中如果任意一对节点i和节点j之间至少存在一条路径,则网络是连通的,若不存在则是不连通的。
集聚系数
集聚系数用以捕获给定节点邻居节点之间的连接程度。对于一个度为ki的节点i,
局部聚集系数被定为
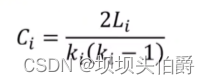
如下图所示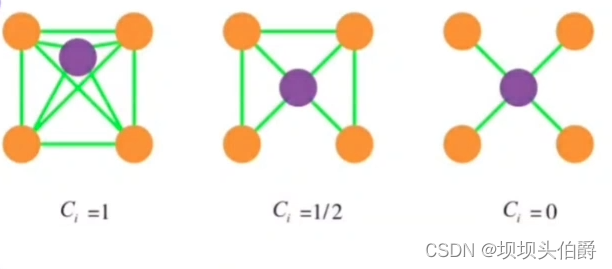
整个网络的集聚程度可以由平均集聚系数所表征,它代表了所有节点的局部集聚系数的平均值
全局集聚系数

度分布
大多数实际网络中的节点的度满足一定的概率分布的。定义p(k)为网络中度为k的节点在整个网络中所占的比例。
规则网络:由于每一个节点具有相同的度,所以其度分布集中在一个单一尖峰上,是一种Delta分布。
完全随机网络:度分布具有泊松分布的形式,每条边出现概率是相等的,大多数节点的度是基本相同的,并接近于网络平均度(k),远离峰值(k),度分布则按指数形式急剧下降。把这类网络称为均匀网络。
累积度分布
可以使用累积度分布函数来描述度分布情况,它与度分布的关系为
P
k
=
∑
x
=
k
∞
P
(
x
)
P_k=\sum_{x=k}^{\infty }P(x)
Pk=x=k∑∞P(x)
它表示度不小于k节点的概率分布。
网络的直径和平均距离
网络中的两节点Vi和Vj之间经历边数最少的一条简单路径(经历的边各不相同),称为测地线。测地线的边数dij称为两节点Vi和Vj之间的距离(或者叫测地线距离)。
1/dij称为节点Vi和Vj之间的效率,记为εij。通常用效率来度量节点之间的信息传递速度。
网络的直径D定义为所有距离dij中最大值
平均距离(特征路径长度)
平均距离L定义为所有节点对之间距离的平均值, 它描述了网络中节点间的平均分离程度。
很多实际网络虽然节点数巨大,但是平均距离却小的惊人,这就是所谓的小世界效应。
度—度相关性
1.基于最近邻平均度值的度-度相关性
度-度相关性描述了网络中度大的节点和度小的节点之间的关系。若度大的节点倾向于和度大的节点连接,则网络是度-度正相关,反之则是度-度负相关。
节点Vi的最近邻平均度值的定义为:
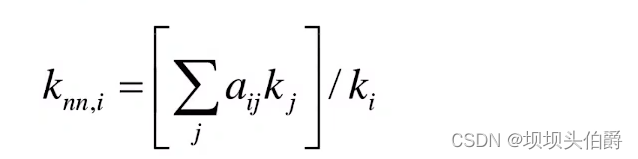
其中ki表示节点Vi的度值,aij为邻接矩阵元素
所有度值为k的节点的最近邻平均度值的平均值为knn(k)定义为
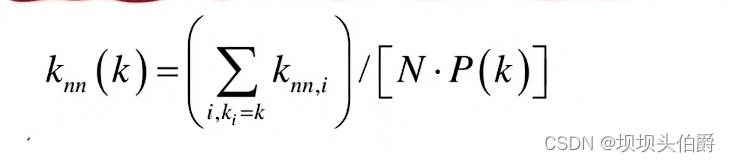
式子中N为节点总数,P(k)为度分布函数
如果knn(k)随着k的上升而上升,则说明度值大的节点倾向于和度值大的节点连接,网络具有正相关特性,称之为同配网络;反之网络具有负相关特性,称之为异配网络。
2.基于Pearson相关系数的度-度相关性
Newman利用边两端节点的度的Pearson相关系数r来描述网络的度-度相关性,定义如下: