基于博弈树的开源五子棋AI教程[3 极大极小搜索]_博弈树五子棋

引子

极大极小搜索是博弈树搜索中最常用的算法，广泛应用于各类零和游戏中，例如象棋，围棋等棋类游戏。算法思想也是合乎人类的思考逻辑的：博弈双方轮流决策，并且认为双方都是理性的，都希望自己的利益最大化或者对手利益最小化。
在介绍算法前，了解博弈树的基本知识是必要的。博弈树的节点代表状态，在五子棋中就代表一个盘面；博弈树的边代表决策，对于五子棋就是落子的位置。博弈树搜索算法就是通过特定的顺序从根节点遍历整个博弈树来找到最佳的决策路径，这一路径在后文被称为PV路径（主要变例路径，Principal Variation）。

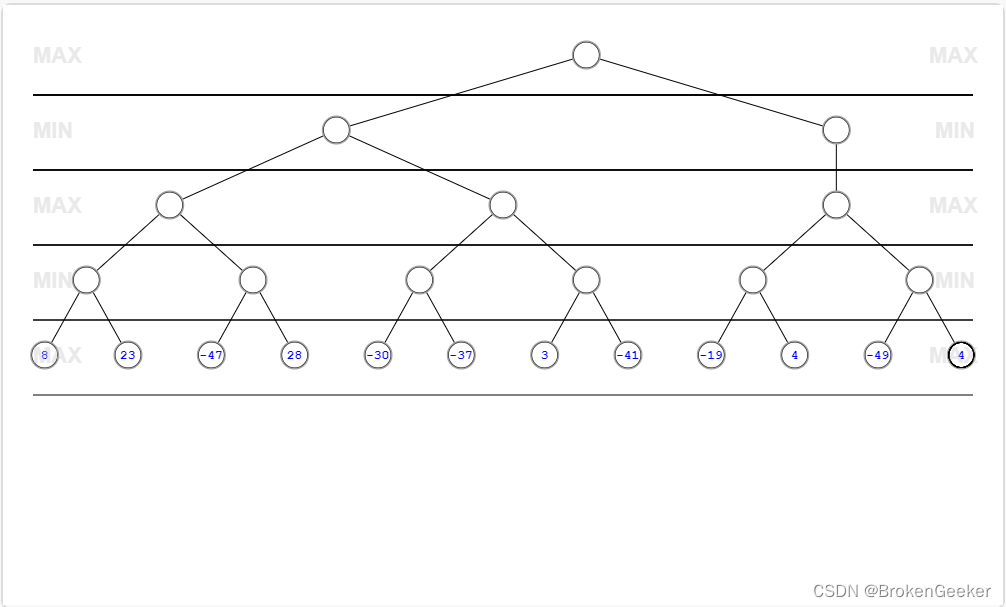
极大极小搜索原理

极大极小搜索双方轮流决策，尽可能的使得己方得分最大化。其将博弈双方命名为Max层和Min层，Max层最大化自己得分，Min层最小化对方得分，然后通过树的深度优先遍历获取PV路径。这里给出wiki中文给出的伪代码。

function  minimax(node, depth, maximizingPlayer) is
    if depth = 0 or node is a terminal node then
        return the heuristic value of node
    if maximizingPlayer then
        value := −∞
        for each child of node do
            value := max(value, minimax(child, depth − 1, FALSE))
        return value
    else (* minimizing player *)
        value := +∞
        for each child of node do
            value := min(value, minimax(child, depth − 1, TRUE))
        return value
1
2
3
4
5
6
7
8
9
10
11
12
13

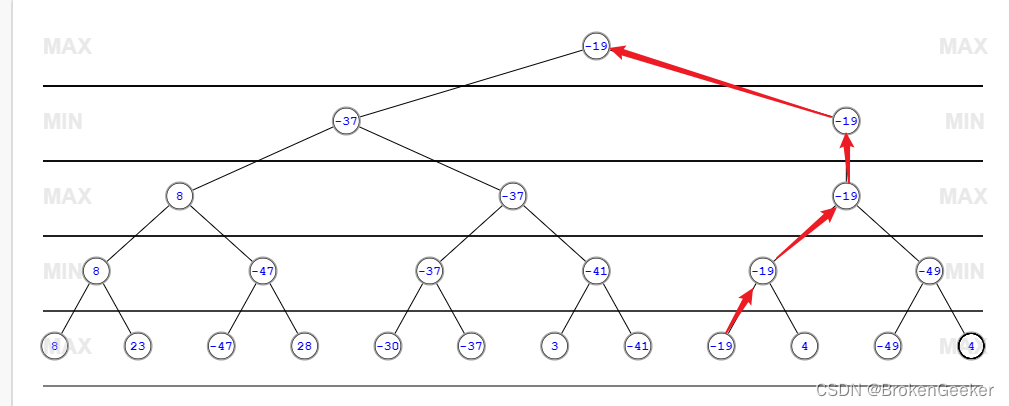
alpha-beta剪枝

五子棋虽然复杂度比不上围棋，在我看到一些文章中指出五子棋的分支因子为35，意味着每个盘面平均有35个合理着法。对于指数膨胀的博弈树，深度加深后，叶子节点的数量是恐怖的，想完整遍历完整个树几乎是不可能完成的事，剪枝算法应运而生。

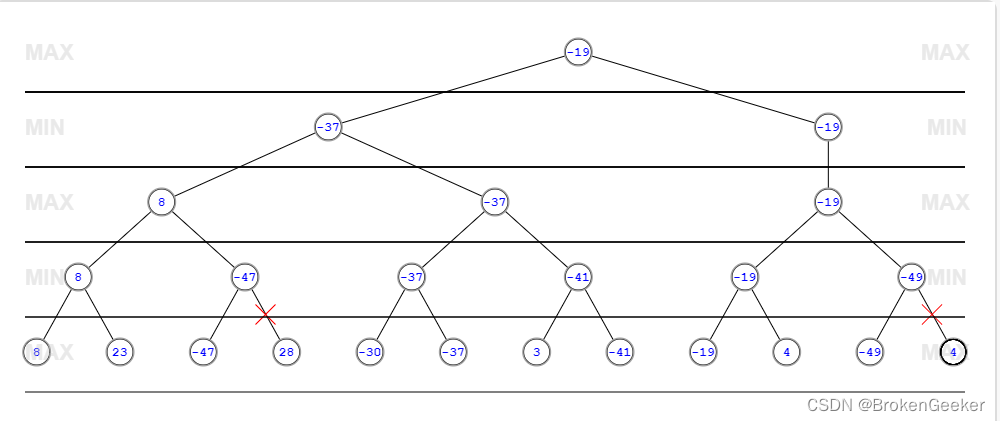
alpha-beta剪枝(AB剪枝)是常见的优化方法，算法可以在保证最终的搜索结果不变的情况下尽可能的减少搜索节点。对于每一个节点都有一个alpha值和beta值来记录从根节点搜索到当前节点获取到的搜索信息，alpha值保存了当前max层玩家最好的走法，beta值记录了max层最坏的走法。当发现最好的走法的得分比最坏走法得分还高是（alpha>=beta）这个节点就应当被裁剪。
这种说法看着比较难以理解，下面给出四个AB剪枝例子来加深概念。

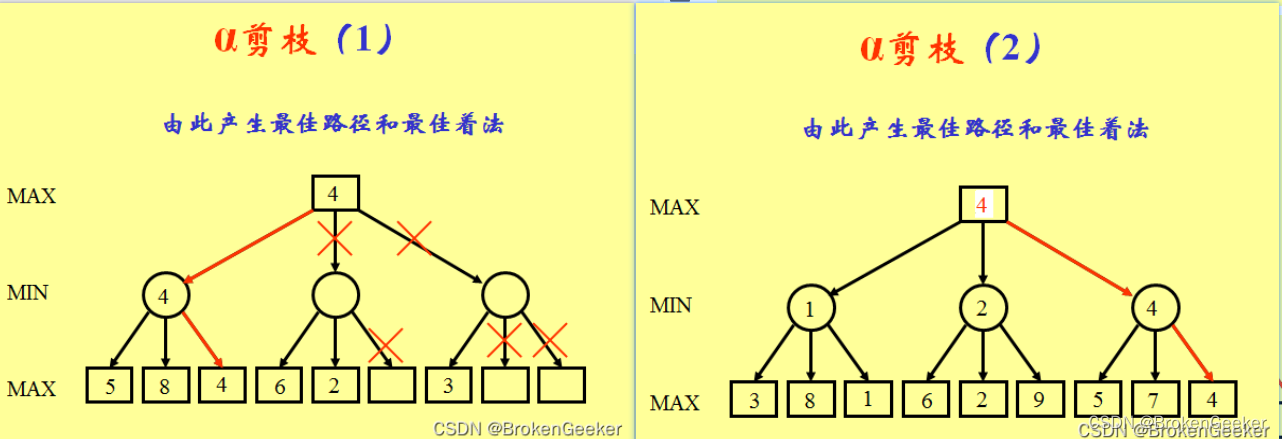
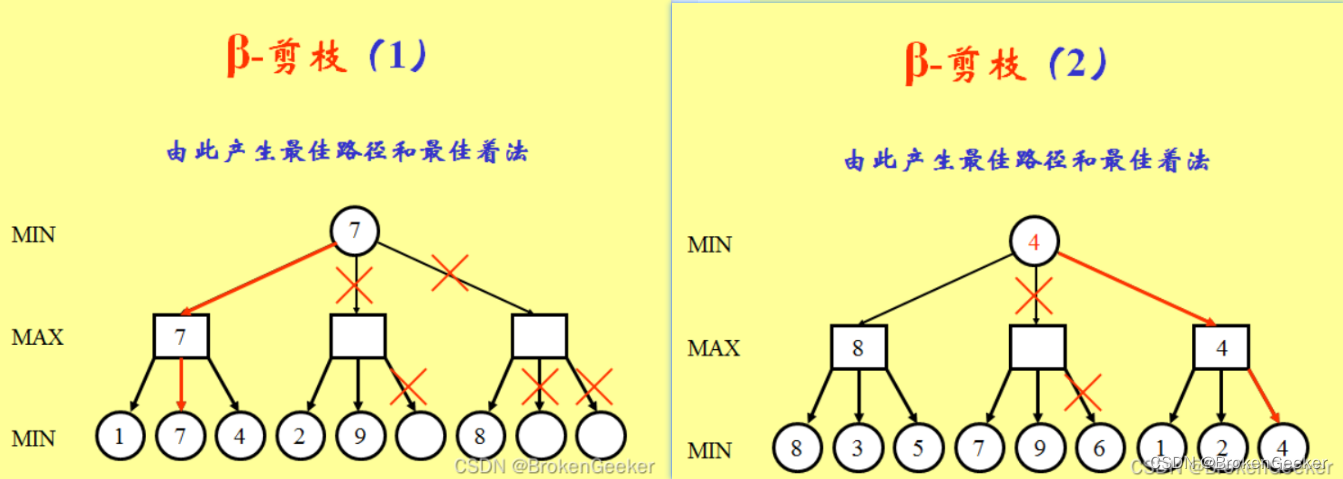
函数 alphaBeta(node, depth, α, β, maximizingPlayer):
    如果 depth = 0 或 node 是一个终端节点:
        返回 node 的评估值

    如果 maximizingPlayer:
        最大值初始化为 -∞
        对于每个子节点 child of node:
            最大值 = max(最大值, alphaBeta(child, depth - 1, α, β, False))
            α = max(α, 最大值)
            如果 β ≤ α:
                跳出循环（剪枝）
        返回 最大值

    否则:
        最小值初始化为 +∞
        对于每个子节点 child of node:
            最小值 = min(最小值, alphaBeta(child, depth - 1, α, β, True))
            β = min(β, 最小值)
            如果 β ≤ α:
                跳出循环（剪枝）
        返回 最小值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

AB剪枝的搜索效率高度依赖子节点顺序，PV路径将更有利于剪枝发生。后面将在启发式搜索中详细介绍节点排序技术。

负极大搜索

极大极小的搜索中需要区分Max，Min玩家，为了代码简约提出了负极大搜索算法。算法认为对于任何一个节点，一个玩家的得分和另一玩家的损失是一样的。

函数 negaMax(node, depth, α, β):
    如果 depth = 0 或 node 是一个终端节点:
        返回 node 的评估值

    最大值初始化为 -∞
    对于每个子节点 child of node:
        分数 = -negaMax(child, depth - 1, -β, -α)
        最大值 = max(最大值, 分数)
        α = max(α, 分数)
        如果 α ≥ β:
            跳出循环（剪枝）
    返回 最大值

1
2
3
4
5
6
7
8
9
10
11
12
13

值得注意的一点，极大极小搜索和负极大搜索的评分函数是不一样。极大极小搜索中，无论是max层最大化自己得分，还是min层最小化对方得分，其评分的视角始终是最大层玩家。然而在负极大搜索中，max层和min层的概念已然不复存在，无论哪一方在进行决策时关注点都是最大化己方得分，因此其评分视角是当前层玩家，而不是最大层玩家。
选择负极大搜索的意义不仅在于代码简约，逻辑清晰，还有最重要的一点是置换表。极大极小搜索中，在交换双方玩家，或者将博弈树中某一中间节点作为根节点（玩家身份发生变化max玩家变成min玩家）时，我们需要考虑很多问题，置换表中的分数是不是合理的？评分视角是不是我们希望的？置换标记位是不是合理的？评分的上界是不是依旧可靠？是不是应该变成下界？但是在负极大搜索中我们就无需考虑，因为无论是分数还是标记位视角都是当前层玩家。由于我们在评分过程中，不同视角不是完全对称，其分数并不是严格相等的，置换表在玩家角色变化时并不是严格安全的，可能会造成不稳定的现象，但是这种变化在我看来时完全可以接受的。

//fail-soft negMax Alpha-Beta pruning search
int GameAI::NABSearch(int depth, int alpha, int beta, bool maximizingPlayer, quint8 searchSpaceType)
{
    int score;
    int evalPlayer = globalParam::AIPlayer;
    MPlayerType searchPlayer = maximizingPlayer ? evalPlayer : UtilReservePlayer(evalPlayer);

    if(zobristSearchHash.getNABTranspositionTable(score, depth, alpha, beta)) {
        return score;
    }

    //  或 游戏结束
    // ??或 分数过大过小
    score = evaluateBoard(evalPlayer);//负极大搜索中评估必须searchPlayer
    if(!maximizingPlayer) score *= -1;

    if (qAbs(score) > globalParam::utilGameSetting.MaxScore || checkSearchBoardWiner() != PLAYER_NONE){
        //保存置换表
        return score;
    }
    // 达到搜索深度
    if (depth == 0){
        //保存置换表
        //VCF
        QList<MPoint> vcf, vcfpath;
        if(VCXSearch(globalParam::utilGameSetting.MaxVctSearchDepth, maximizingPlayer, VCT_SEARCH, vcf, vcfpath)){
            qDebug() << "NABsearch : find vct";
            if(maximizingPlayer) return globalParam::utilGameSetting.MaxScore;
            else return -globalParam::utilGameSetting.MaxScore;
        }
        return score;
    }

    // 着法生成
    QVector<MPoint> searchPoints;
    getSortedSearchSpace(searchPoints, evalPlayer, searchPlayer, searchSpaceType);

    int scoreBest = -INT_MAX;
    int hashf = hashfUperBound;
    MPoint moveBest(InvalidMPoint);
    quint16 savedSearchBoardPatternDirection[boardSize][boardSize];

    for (const auto &curPoint : searchPoints) {
        if (!searchBoardHasPiece(curPoint)) {
            setSearchBoard(curPoint, searchPlayer, savedSearchBoardPatternDirection);// searchPlayer落子
            score = -NABSearch(depth - 1, -beta, -alpha, !maximizingPlayer,searchSpaceType);
            setSearchBoard(curPoint, PLAYER_NONE, savedSearchBoardPatternDirection);// 撤销落子

            if (score > scoreBest) {
                scoreBest = score;
                moveBest = curPoint;
                if (score >= beta) {
                    hashf = hashfLowerBound;
                    appendSearchKillerTable(curPoint, depth, hashf);
                    aiCalInfo.cutTreeTimesCurrentTurn ++;
                    break; // Alpha-Beta 剪枝
                }
                if (score > alpha) {
                    alpha = score;
                    hashf = hashfExact;
                }
            }
        }
    }
    //更新历史表
    appendSearchHistoryTable(moveBest, depth, hashf);
    // 更新置换表
    zobristSearchHash.appendNABTranspositionTable(depth, scoreBest, hashf, moveBest, UtilReservePlayer(searchPlayer));

    return scoreBest;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

尾记

最后本来想讨论下AB剪枝中fail-soft和fail-hard的区别的，限于篇幅就以参考文档的方式放在后面。其次是没有展开AB值的更新以及为什么要剪枝的实际含义，展开说容易绕晕，没有几个合适的例子理解的快。
理解AB剪枝搜索是博弈树搜索的基石，后面利用置换表，杀手表以及多线程加速搜索有这重要的作用。
关于fail-hard和fail-soft的讨论
MTD+置换表
wiki AB剪枝
Minmax 搜索动画