基于Matlab的图像去噪算法仿真

基于Matlab的图像去噪算法仿真

在信息化的社会里，图像在信息传播中所起的作用越来越大。所以，消除在图像采集和传输过程中而产生的噪声，保证图像受污染度最小，成了数字图像处理领域里的重要部分。

本文主要研究分析邻域平均法、中值滤波法、维纳滤波法及模糊小波变换法的图像去噪算法。首先介绍图像处理应用时的常用函数及其用法；其次详细阐述了四种去噪算法原理及特点；最后运用Matlab软件对一张含噪图片（含高斯噪声或椒盐噪声）进行仿真去噪，通过分析仿真结果得出：

一．均值滤波是典型的线性滤波，对高斯噪声抑制是比较好的；

二．中值滤波是常用的非线性滤波方法，对椒盐噪声特别有效；

三．维纳滤波对高斯噪声有明显的抑制作用；

四．对小波系数进行阈值处理可以在小波变换域中去除低幅值的噪声和不期望的信号。

本论文主要是从两方面展开，首先是图像去噪算法：简要说明了图像噪声的概念及分类，详细阐述了邻域平均法、中值滤波法、维纳滤波法及模糊小波变换法的去噪原理及特点。

其次是基于Matlab的图像去噪算法仿真：根据邻域平均法、中值滤波法、维纳滤波法及模糊小波变换法原理分析，运用Matlab仿真软件编写代码，对一张含噪图片（含高斯噪声或椒盐噪声）进行仿真去噪，并对结果分析讨论，比较几种方法的优缺点。

本论文仿真时选取一张彩色图片“2010-03-09-2.bmp”，并在图片中加入两种噪声：高斯噪声和椒盐噪声。所谓高斯噪声是指它的概率密度函数服从高斯分布的一类噪声。椒盐噪声是由图像传感器、传输信道、解码处理等产生的黑白相间的亮暗点噪声，属于非平稳噪声。本章利用Matlab软件对含噪图像的去噪算法进行仿真，将应用邻域平均法、中值滤波法、维纳滤波法和模糊小波变换法对含有高斯噪声和椒盐噪声图像的去噪效果进行比较，从而得到相应结论。

邻域平均法的仿真

本节选用邻域平均法对含有高斯噪声和椒盐噪声的图片进行去噪，并用Matlab软件仿真。

（1）给图像加入均值为0，方差为0.02的高斯噪声，选择3×3模板去噪

Matlab部分代码：

j=imnoise(x,'gaussian',0,0.02);

h=ones(3,3);

h=h/9;

k=conv2(j,h);

仿真结果如图4-1所示。

图1-1 邻域平均法对高斯噪声去噪的仿真结果

（2）给图像加入噪声密度为0.02的椒盐噪声，选择3×3模板去噪

Matlab部分代码：

j=imnoise(x,'salt & pepper',0.02);

h=ones(3 3);

h=h/9;

k=conv2(j,h);

仿真结果如图1-2所示。

图1-2 邻域平均法对椒盐噪声去噪的仿真结果

从仿真结果可以看出：邻域平均法实现起来很方便，适用于消除图像中的颗粒噪声，但需要指出这种方法既平滑了图像信号，同时使图像的细节部分变得模糊。由以上处理后的图像可以看到：邻域平均法消弱了图像的边缘，使图像变得有些模糊。如图1-1所示，均值滤波对高斯噪声的抑制是比较好的，但对椒盐噪声的抑制作用不好，如图1-2所示，椒盐噪声仍然存在，只不过被削弱了而已。为了改善均值滤波细节对比度不好、区域边界模糊的缺陷，常用门限法来抑制椒盐噪声和保护细小纹理，用加权法来改善图像的边界模糊，用选择平均的自适应技术来保持图像的边界。

中值滤波的仿真

本节选用中值滤波法对含有高斯噪声和椒盐噪声的图像进行去噪，并用Matlab软件仿真。

（1）给图像加入均值为0，方差为0.02的高斯噪声，分别选择3×3模板、5×5模板和7×7模板进行去噪

Matlab部分代码：

j=imnoise(I,'gaussian',0,0.02);

x=j(:,:,1);

subplot(221);

imshow(x);

title('高斯噪声图片');

k1=medfilt2(x,[3 3]);

k2=medfilt2(x,[5 5]);

k3=medfilt2(x,[7 7]);

仿真结果如图1-3所示。

图1-3 中值滤波法对高斯噪声去噪的仿真结果

（2）给图像加入噪声密度为0.02的椒盐噪声，分别选择3×3模板、5×5模板和7×7模板进行去噪

Matlab部分代码：

i=imread('2.bmp');

j=imnoise(I,'salt & pepper',0.02);

x=j(:,:,1);

subplot(221);

imshow(x);

title('椒盐噪声图片');

k1=medfilt2(x,[3 3]);

k2=medfilt2(x,[5 5]);

k3=medfilt2(x,[7 7]);

仿真结果如图1-4所示。

图1-4 中值滤波法对椒盐噪声去噪的仿真结果

从仿真结果可以看出：对图像加入椒盐噪声后，应用中值滤波，如图1-4所示，噪声的斑点几乎全部被滤去，它对滤除图像的椒盐噪声非常有效。而对于高斯噪声来说，如图1-3所示，虽然也有一些去噪效果，但效果不佳。由此可知，中值滤波法运算简单，易于实现，而且能较好地保护边界，但有时会失掉图像中的细线和小块区域。并且采用窗口的大小对滤波效果影响很大，窗口越大，图像去噪效果越好，但代价是模糊的程度越大。

维纳滤波的仿真

选用维纳滤波法对含有高斯噪声和椒盐噪声的图像进行去噪，并用Matlab软件仿真。

（1）给图像加入均值为0，方差为0.02的高斯噪声，选择3×3模板去噪

Matlab部分代码：

i=imread('2.bmp');

j=imnoise(I,'gaussian',0,0.02);

x=j(:,:,1);

k=wiener2(x);

仿真结果如图1-5所示。

图1-5 维纳滤波法对高斯噪声去噪的仿真结果

（2）给图像加入噪声密度为0.02的椒盐噪声，选择3×3模板去噪

Matlab部分代码：

j=imnoise(I,'salt & pepper',0.02);

x=j(:,:,1);

k=wiener2(x);

仿真结果如图1-6所示。

图1-6 维纳滤波法对椒盐噪声去噪的仿真结果

从仿真结果可以看出：维纳滤波对高斯白噪声的图像滤波与邻域平均法比较， 滤波效果好，它比线性滤波器具有更好的选择性，可以更好地保存图像的边缘和高频细节信息。虽然，维纳滤波在大多数情况下都可以获得满意的结果，尤其对含有高斯噪声的图像。另外维纳滤波对于椒盐噪声去除效果却不尽人意，几乎没有效果。它不能用于噪声为非平稳的随机过程的情况，对于向量情况应用不方便。因此，维纳滤波在实际问题中应用不多。

基于模糊小波变换法的仿真

选用模糊小波变换法对含有高斯噪声和椒盐噪声的图像进行去噪，并用Matlab软件仿真。

（1）给图像加入均值为0，方差为0.02的高斯噪声，用小波函数coif2对图象进行2层分解，选择3×3模板去噪

Matlab部分代码：

function y=zishiying(x)

x11=medfilt2(x,[3 3]);

x12=double(x11);

[a,b]=size(x12);

[c,s]=wavedec2(x12,3,'coif2');

n=[1,2,3];

p4=0.02*(sqrt(2*log(a*b)));

size(detcoef2('h',c,s,1));

size(detcoef2('v',c,s,1));

size(detcoef2('d',c,s,1));

p1(1)=detcoef2('h',c,s,1);

p2(1)=detcoef2('v',c,s,1);

p3(1)=detcoef2('d',c,s,1);

p1(2)=detcoef2('h',c,s,2);

p2(2)=detcoef2('v',c,s,2);

p3(2)=detcoef2('d',c,,s,2);

for i=1:1:2

p1(i)=1/((p1(i)-p4)^2+1);

if p1(i)>=p4

p1(i)=sign(p1(i))*(abs(p1(i))-p1(i)*p4);

else

p1(i)=0;

end

if p2(i)>=p4

p2(i)=sign(p2(i))*(abs(p2(i))-p2(i)*p4);

else

p2(i)=0;

end

if p3(i)>=p4

p3(i)=sign(p3(i))*(abs(p3(i))-p3(i)*p4);

else

p3(i)=0;

end

end

仿真结果如图1-7所示。

图1-7 模糊小波变换法对高斯噪声去噪的仿真结果

（2）给图像加入噪声密度为0.02的椒盐噪声，选择3×3模板去噪

仿真结果如图1-8所示。

图1-8 模糊小波变换法对椒盐噪声去噪的仿真结果

从仿真结果可以看出：为验证本文算法的滤波效果，对加入不同噪声的图像进行了滤波测试。从视觉来看，自适应模糊小波变换算法在保持细节和去噪两方面效果最好。在平滑高斯噪声和有脉冲噪声的图像去噪效果都很显著。本算法相对于其它几种算法其效果都有明显的改进，既能够很好地消除噪声，又能够较好地保持图像边缘细节，而且算法简单，易于实现。目前使用比较广泛。

几种去噪方法的比较分析

均值滤波是典型的线性滤波算法，其采用的主要方法为邻域平均法。即对待处理的当前像索点

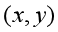
，选择一个模板，该模板由其近邻M个像素组成，求模板中所有像素的均值，再把该均值赋予当前像素的算术平均值

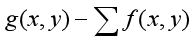
，作为邻域平均处理后的灰度。该方法运算简单，对高斯噪声具有良好的去噪能力。均值滤波可归结为矩形窗加权的有限冲激响应线性滤波器。因此，均值滤波相当于低通滤波器。这种低通性能在平滑噪声的同时，必定也会模糊信号的细节和边缘，即在消除噪声的同时也会对图像的高频细节成分造成破坏和损失，使图像模糊，由以上处理后的图像可以看到：邻域平均法消弱了图像的边缘，使图像变得有些模糊。均值滤波时高斯噪声抑制是比较好的，但对椒盐噪声的抑制作用不好，椒盐噪声仍然存在，只不过被削弱了而已，如仿真结果图1-2所示。为了改善均值滤波细节对比度不好、区域边界模糊的缺陷，常用门限法来抑制椒盐噪声和保护细小纹理，用加权法来改善图像的边界模糊，用选择平均的自适应技术来保持图像的边界。

中值滤波是常用的非线性滤波方法，也是图像处理技术中最常用的预处理技术。它可以克服线性滤波器给图像带来的模糊，在有效清除颗粒噪声的同时，又能保持良好的边缘特性，从而获得较满意的滤波效果，特别适合于去除图像的椒盐噪声，如仿真结果图1-4所示。当窗口在图像中上下左右进行移动后，利用中值滤波算法可以很好地对图像进行平滑处理。由以上图像可以看到：中值滤波法较好地保留了图像的边缘，使其轮廓比较清晰。中值滤波对椒盐噪声特别有效，取得了很好的效果，而对高斯噪声效果不佳。对一些复杂的图像，可以使用复合型中值滤波，如：中值滤波线性组合、高阶中值滤波组合、加权中值滤波以及迭代中值滤波等来改善单纯中值滤波的一些不足，从而达到更好的滤波效果。

维纳滤波是一种对退化图像进行恢复处理的一种常用算法，也是最早也最为人们熟知的线性图像复原方法。其设计思想是使输人信号乘响应后的输出，与期望输出的均方误差为最小。从图1-5中可以看到维纳滤波对高斯噪声有明显的抑制作用，相对与均值滤波和中值滤波，维纳滤波对这两种噪声的抑制效果更好，缺点就是容易失去图像的边缘信息。又正如图1-6所示，维纳滤波对椒盐噪声几乎没有抑制作用。

小波阈值去噪方法是研究最广泛的方法。这种非线性滤波方法之所以特别有效， 就是由于小波变换具有一种“ 集中”的能力， 它可以使一个信号的能量在小波变换域集中在少数系数上， 因此这些系数的幅值必然大于在小波变换域内能量分散于大量小波系数上的信号或噪声的幅值。这就意味着对小波系数进行阈值处理可以在小波变换域中去除低幅值的噪声和不期望的信号， 然后运用小波逆变换， 得到去噪后的重建图像。如图1-7、1-8所示，使用小波变换都得到了较好的消噪效果。

上述滤波方法虽都有一定的降噪效果，但都有其局限性。事实上，不管滤波器具有什么样的频率响应，均不可能做到噪声完全滤掉，使信号波形不失真。但我们可以不断地改进滤波的技术，如实际应用中常用一些改进型的滤波方法如小波导向、多级门限检测来提高去噪的效果从而最大可能地恢复出原始图像。

参考文献：

[1] CAITT,SILVERMANBW．Incorporating information on Neighbouring Coefficients into wavelet estimation [J]．The Indian Journal of Statistics，2011，63(2)：127-148．

[2] 杨群生，陈敏等．基于模糊技术的随机噪声消除算法[J]．华南理工大学学报，2010，28(8)：82-87．

[3] L.K.Shark and C.Yu.Denoising by optimal fuzzy thresholding in wavelet domain [J]．IEEE Electronics letters，2010，36(6)：581-582．

[4] S.Mallat，Sifen Zhong，Characterization of signals from multiscale edges[J]．IEEE Trans on PAMI，2002，PAMI-14(7)：710-732．

[5] Keesok J.Han and Ahmed H.Tewfik.Hybnd Wavelet Transform Fllter for Image Recovery[J]．IEEETrans．Image Processing，2010，l540-544．

[6] H.K .Kwan .Fuzzy filters for noise image filtering [J]．IEEE．2013，161-164．

[7] 杨晋生，蔡靖等.一种具有鲁棒性的基于小波变换的滤波方法[J].电子与信息学报，2012，24（3）：413-417．

[8] 张磊，潘泉，张洪才等.小波域滤波阈值参数的选取[J].电子学报，2011，29（3）：400-402．