建堆的时间复杂度和堆排序_建堆时间复杂度

建堆的时间复杂度

下面都以建大堆演示

向下调整建堆

void Adjustdown(HPDataType* a, int size,int parent)
{
	int child = parent * 2 + 1;
	while (child < size)
	{
		if (child+1<size&&a[child + 1] >a[child])
		{
			child++;
		}
		if (a[parent] <a[child])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

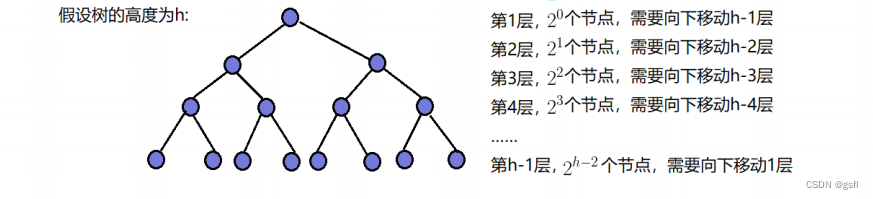
我们根据求堆的节点总数（利用等比数列求和公式）可以知道堆节点总数N和堆高度h之间的关系：N=2^h-1。再根据图片规律求出移动节点的步数：

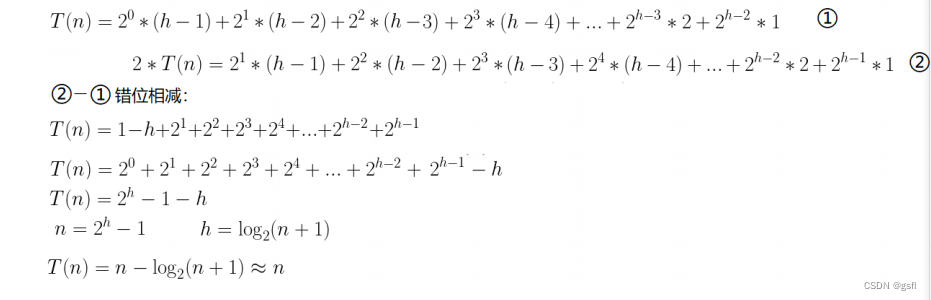
因此，利用向下调整建堆的的时间复杂度为O（N）。

向上调整建堆

void Adjustup(HPDataType*a,int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[parent] < a[child])
		{
			Swap(&a[parent], &a[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

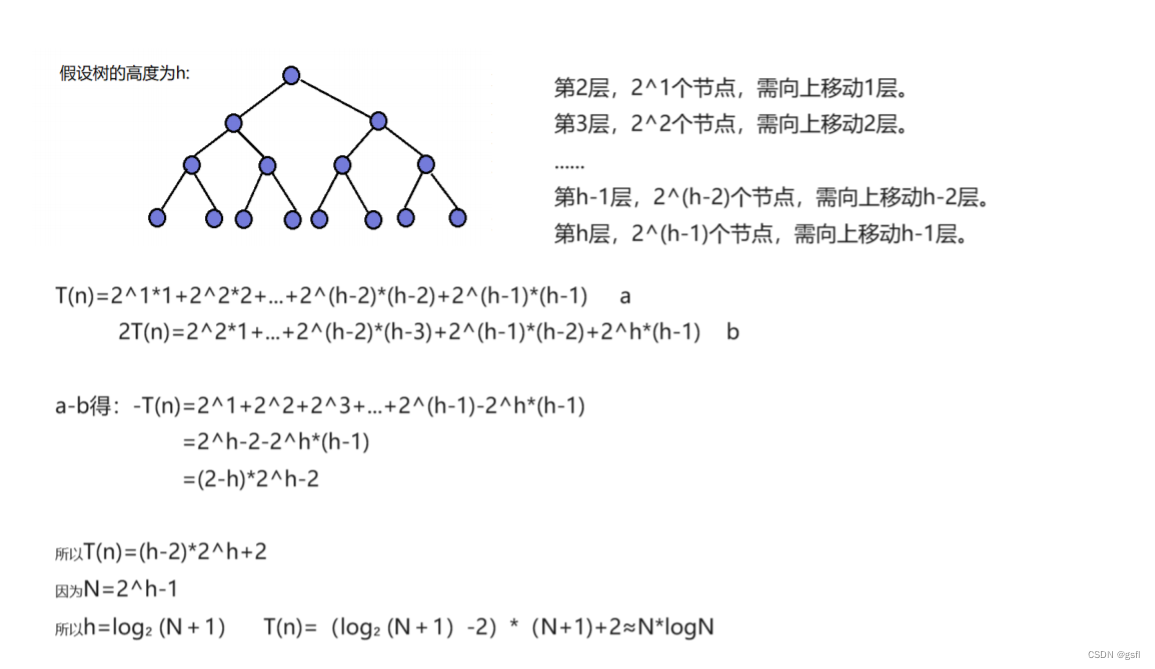
对比两种建堆的时间复杂度我们能看出向下调整建堆要优于向上调整建堆，接下来我实现堆排序。

堆排序

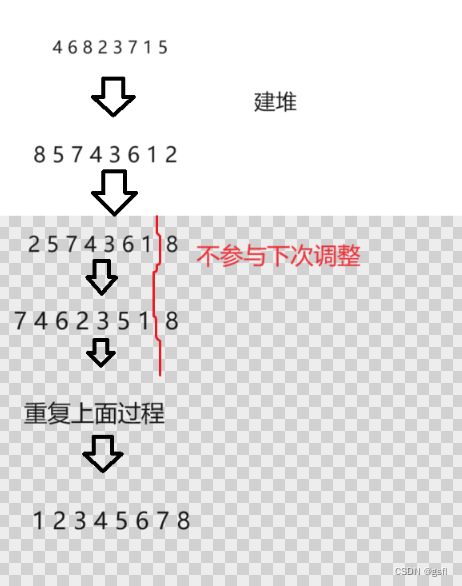
排序可以分为升序排序和降序排序，实现堆排序前，我们先要思考，升序和降序哪种适合大堆，哪种适合小堆？假如我们现在要实现升序排序，我们可以先用小堆理一遍思路，小堆结构是堆顶元素最小，如果我们直接把堆顶拿出来，那么下面父子兄弟节点的关系全乱了，最差的情况需要把每个节点都向上调整一遍，时间复杂度太高。如果选择大堆，我们只需把每次堆顶的元素和堆中最后一个元素交换，然后让新的堆顶向下调整，（每次交换完后最后的元素不参与后续的向下调整）就能得到一个升序的数组。

void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void Heapsort(int *a,int n)
{
	for (int i = 1; i < n; i++)
	{
		Adjustup(a, i);
	}
	int end = n - 1;
	while (end>0)
	{
		Swap(&a[0], &a[end]);
		Adjustdown(a, end, 0);
		--end;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

先建一个大堆，然后不断将堆顶和堆尾元素交换，再让新堆顶向下调整得到次大的数

实现

int main()
{
	int a[] = { 4,6,8,2,3,7,1,5 };
	Heapsort(a, sizeof(a) / sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11