热门标签
热门文章
- 1HDFS常用命令_hdfs get命令
- 2【C语言/数据结构】栈:从概念到两种存储结构的实现
- 3基于springboot+vue的汽车租赁管理系统,附源码+数据库+论文+PPT,适合课程设计、毕业设计_车辆租赁管理系统数据库
- 4Android OpenCV实现人脸检测(一)完成人脸检测功能_android opencv做小区门禁人脸识别
- 5.NET开源、功能强大、跨平台的图表库
- 6Linux 进程间通信——消息队列_linux消息队列
- 7PDF控件Spire.PDF for .NET【安全】演示:使用文本或/和图像对 PDF 进行数字签名
- 8C++ ─── 匿名对象+变量的创建顺序
- 9前端实现录音
- 10求第k大数_求第k大数的时间复杂度nlogn
当前位置: article > 正文
Pytorch:自适应激活函数(Adaptive activation functions),让网络更容易收敛
作者:Gausst松鼠会 | 2024-05-17 07:16:33
赞
踩
自适应激活函数
最近看了一篇文章,里面介绍了自适应的激活函数,它可以使得网路收敛速度更快。
文章:《Adaptive activation functions accelerate convergence in deep and physics-informed neural networks》
激活函数是深度学习中至关重要的部分,我们在做深度学习的时候通常会利用激活函数增加网络的非线性能力,使其能够拟合更复杂的情况,比较熟悉的有ReLU,Tanh,Sigmoid等等,但是这些激活函数在某些情况下并不是最合适的,甚至会出现梯度消失或者梯度爆炸的情况,于是作者提出了自适应的激活函数,来加速网路收敛并且提高稳定性。
简而言之,就是在激活函数里加入了可训练的参数,让普通激活函数的斜率或者角度发生改变,使其更加符合网络参数。
这里我们用Sigmoid举个例子,图来源文章
Sigmoid: 
自适应Sigmoid: 
其中a就是可以改变激活函数slope的超参数,是可以通过网络动态训练的。
下图是不同a下sigmoid函数的形态:

我利用之前写的全连接网络的例子进行测试,把ELU激活函数改为自适应的:
完整代码请参考我之前的文章:Pytorch:手把手教你搭建简单的全连接网络_pytorch 全连接网络_无知的吱屋的博客-CSDN博客
- class DNN(nn.Module):
- def __init__(self,AAF = False):
- super().__init__()
- layers = [1,20,1] #网络每一层的神经元个数,[1,10,1]说明只有一个隐含层,输入的变量是一个,也对应一个输出。如果是两个变量对应一个输出,那就是[2,10,1]
- self.layer1 = nn.Linear(layers[0],layers[1]) #用torh.nn.Linear构建线性层,本质上相当于构建了一个维度为[layers[0],layers[1]]的矩阵,这里面所有的元素都是权重
- self.layer2 = nn.Linear(layers[1],layers[2])
- self.elu = nn.ELU() #非线性的激活函数。如果只有线性层,那么相当于输出只是输入做了了线性变换的结果,对于线性回归没有问题。但是非线性回归我们需要加入激活函数使输出的结果具有非线性的特征
- #可训练的自适应激活函数slope
- if AAF:
- self.a = nn.Parameter(torch.FloatTensor([0.1]))
- else:
- self.a = 1
- def forward(self,d):#d就是整个网络的输入
- d1 = self.layer1(d)
- d1 = self.elu(10*self.a*d1)#每一个线性层之后都需要加入一个激活函数使其非线性化。
- d2 = self.layer2(d1)#但是在网络的最后一层可以不用激活函数,因为有些激活函数会使得输出结果限定在一定的值域里。
- return d2

其中 self.a 就是我们对原始网络加入自适应的因子
d1 = self.elu(10*self.a*d1)
在这样的基础之上再去进行测试发现收敛能力确实提升了很多,并且收敛更好了。
下图是训练曲线,上面没有利用自适应激活函数,下面利用了自适应激活函数。

![]()
可以明显看到,使用了自适应激活函数之后,网络收敛速度加快了很多,并且能够收敛到更低的水平。
最后是回归的结果,同样的,上边是没有利用自适应激活函数,下边是利用率自适应激活函数的结果。利用自适应激活函数之后,我们很明显地能够看出拟合得更好了
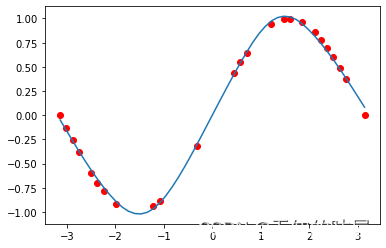

总结:自适应激活函数可以加快收敛,并且使网络收敛更好。
详细的内容可以去看原文章《Adaptive activation functions accelerate convergence in deep and physics-informed neural networks》
实验室网址:CIG | zhixiang
Github网址:ProgrammerZXG (Zhixiang Guo) · GitHub
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/Gausst松鼠会/article/detail/582528
推荐阅读
相关标签


