【MATLAB应用】去噪算法_matlab图像去噪方法

01.引言

图像的产生是电子和光学相互作用的结果，而图像中的噪声则是由于成像过程中的颗粒性质而客观存在的。不同类型的噪声从不同的视角产生，各自具有特点。因此，有效地去除图像中的噪声以获得更高质量的图像具有实际意义。目前存在多种图像去噪方法，包括基于空间域、变换域、偏微分方程模型和形态学等方法。通常，图像去噪的一般过程包括以下步骤：

1. 确定噪声模型：首先根据实际图像的情况，确定噪声的数学模型，这有助于理解和建模噪声的特性。
2. 估计参数：估计噪声模型中的必要参数，这些参数将在后续步骤中用于选择合适的去噪方法。
3. 选择去噪方法：根据噪声类型选择适当的去噪方法。常见的方法包括基于空间域的方法、基于变换域的方 法、基于偏微分方程模型的方法以及基于形态学的方法。
4. 衡量评价：最后，评估图像去噪的效果。这可以通过比较去噪后的图像与原始图像之间的差异来实现。

基于常见的噪声类型，本章将重点研究基于变换域的小波分析方法进行图像去噪。小波变换具有在时频域上提供有效表示的优势，因此在图像去噪中得到了广泛应用。通过在小波域对图像进行分析和处理，可以更好地保留图像的结构信息并去除噪声。

02.模拟噪声的生成

    01.引言
图像的产生是电子和光学相互作用的结果，而图像中的噪声则是由于成像过程中的颗粒性质而客观存在的。不同类型的噪声从不同的视角产生，各自具有特点。因此，有效地去除图像中的噪声以获得更高质量的图像具有实际意义。目前存在多种图像去噪方法，包括基于空间域、变换域、偏微分方程模型和形态学等方法。通常，图像去噪的一般过程包括以下步骤：
 
确定噪声模型：首先根据实际图像的情况，确定噪声的数学模型，这有助于理解和建模噪声的特性。
估计参数：估计噪声模型中的必要参数，这些参数将在后续步骤中用于选择合适的去噪方法。
选择去噪方法：根据噪声类型选择适当的去噪方法。常见的方法包括基于空间域的方法、基于变换域的方   法、基于偏微分方程模型的方法以及基于形态学的方法。
衡量评价：最后，评估图像去噪的效果。这可以通过比较去噪后的图像与原始图像之间的差异来实现。
基于常见的噪声类型，本章将重点研究基于变换域的小波分析方法进行图像去噪。小波变换具有在时频域上提供有效表示的优势，因此在图像去噪中得到了广泛应用。通过在小波域对图像进行分析和处理，可以更好地保留图像的结构信息并去除噪声。
 
02.模拟噪声的生成
clc;clear;close all;
% 在原始图像中加入Gaussian白噪声，椒盐噪声和乘性噪声。图像来源为参考文献[11]
f=imread('Fig4-1(a)original_pattern.tif');
m=64/255;
var = 400/255^2;
g_gauss=imnoise(f,'gaussian',m,var);
d = 0.05;%d表示噪声强度
g_salt = imnoise(f,'salt & pepper',d);
v = 0.06; 
g_speckle = imnoise(f,'speckle', v);
% 显示加噪图像
figure
subplot(2,2,1), imshow(f),title('原始图像');
subplot(2,2,2), imshow(g_gauss), title('Guassian 噪声图像');
subplot(2,2,3), imshow(g_salt), title('椒盐噪声图像');
subplot(2,2,4), imshow(g_speckle), title(' speckle 噪声图像');
%图像存储
% imwrite(g_gauss,'Fig4-1(b)Nguass.jpg','jpg');
% imwrite(g_salt,'Fig4-1(c)Nsalt.jpg','jpg');
% imwrite(g_speckle,'Fig4-1(d)Nspeckle.jpg','jpg');
%显示直方图
figure(2)
subplot(2,2,1), imhist(f),title('原始图像的灰度直方图');
subplot(2,2,2), imhist(g_gauss),title('Guassian 噪声图像的直方图');
subplot(2,2,3), imhist(g_salt),title('椒盐噪声图像的直方图');
subplot(2,2,4), imhist(g_speckle),title('speckle噪声图像的直方图');
 
 
03.基于小波的去噪方法
1.基于模极大值去噪算法效果图
 
2.基于小波阈值去噪算法效果图（软硬阈值）
 
3.相关性去噪效果
 

03.基于小波的去噪方法

1.基于模极大值去噪算法效果图

2.基于小波阈值去噪算法效果图（软硬阈值）

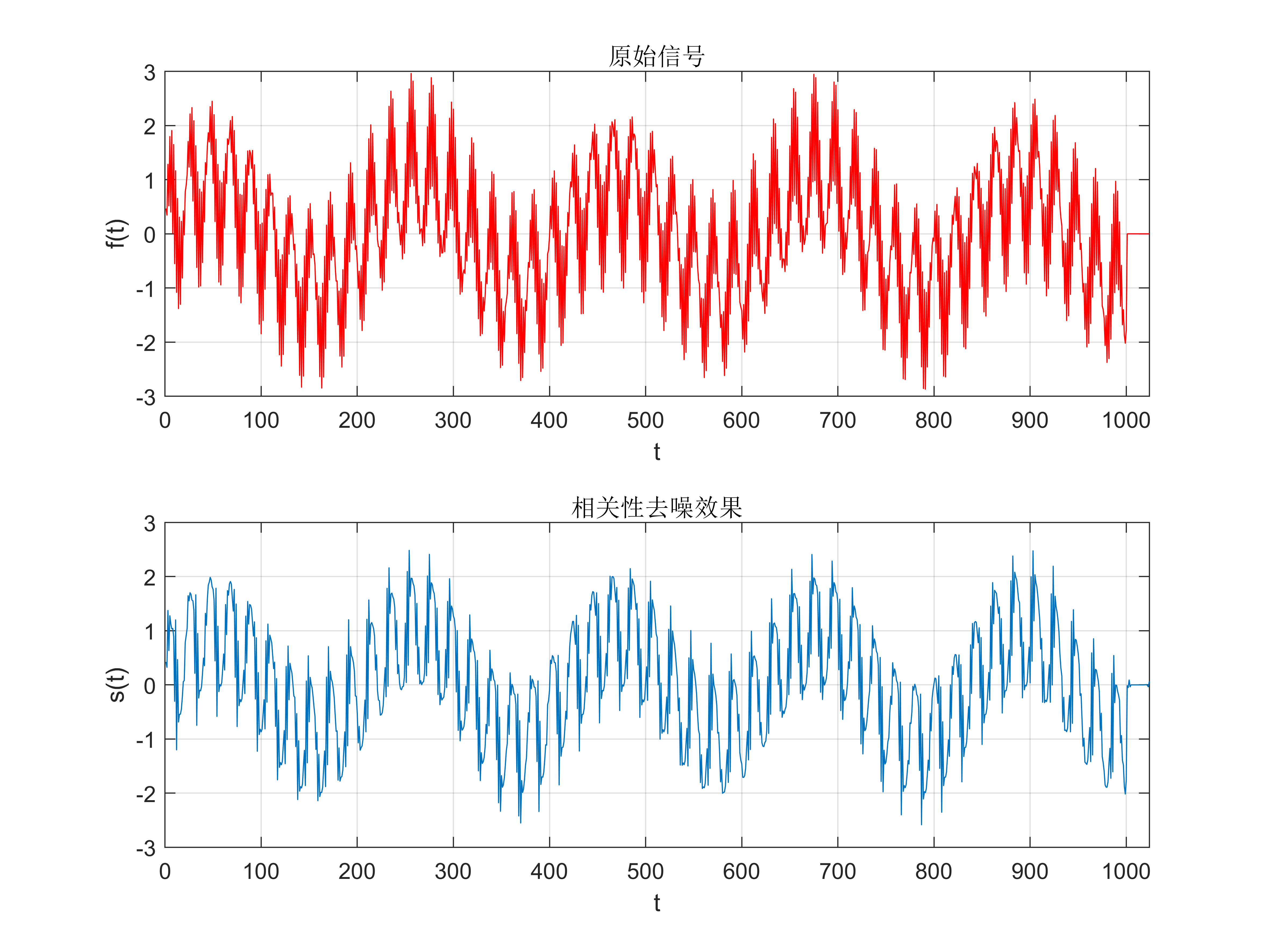
3.相关性去噪效果

获取代码请关注MATLAB科研小白的个人公众号（即文章下方二维码），并回复MATLAB应用

本公众号致力于解决找代码难，写代码怵。各位有什么急需的代码，欢迎后台留言~不定时更新科研技巧类推文，可以一起探讨科研，写作，文献，代码等诸多学术问题，我们一起进步。