【读书笔记-＞统计学】02-01 各种“平均数”-均值、中位数和众数概念简介_均值符号

各种“平均数”

在这之前，请大家先要知道这里的“平均数”可不指代平常的概念，在统计学中，平均数可以帮我们把握一批数据的总体情况。

均值

均值，就是我们日常生活中经常用到的平均数，只需要将所有数字加起来除以数字个数即可。

如果用字母（抽象化）来表示均值：

$$\mu =\frac{\sum x}{n}$$

其中$\mu$是均值的专用符号，读作“缪”。$\Sigma$为求和符号，读作“西格玛”。x为每个数字，n为数字的个数。

对于有频数的情况，比如计算平均年龄，19岁的1个，20岁的3个，21岁的1个。

$\mu =\frac{\sum fx}{\sum f}=\frac{1\ast 19+3\ast 20+1\ast 21}{5}=20$

$f$表示某个数字的频数。首先每个数字乘以其频数，然后将全部乘积相加，之后除以频数之和。

异常值

给出一个情境：如果有一个中年人想要进入一个由中年人组成的健身班，按照均值的计算，有3个班，平均年龄分别是17、25和38。如果选择第3个班级，看起来是合理的，但遗憾的是，它其实是这样的一个班级。

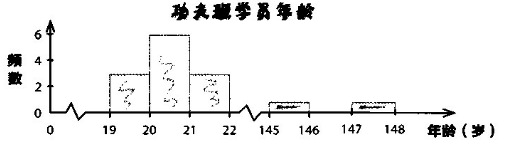
有两个祖师爷，分别是145岁和147岁，这会导致计算出来的均值在38岁，但实际上大部分人在20岁左右。

我们称最右边的值为异常值，因为大部分的学员年龄都在20岁左右，因为异常值的存在，导致平均值整体右偏到38岁，实际上根本没有人38岁。祖师爷的存在使得均值被抬高了。这种情况也叫数据偏斜了。

异常值：与其他数据格格不入的极高或极低的数值

偏斜数据：当异常值将数据向左或者向右“拉”时即产生偏斜数据

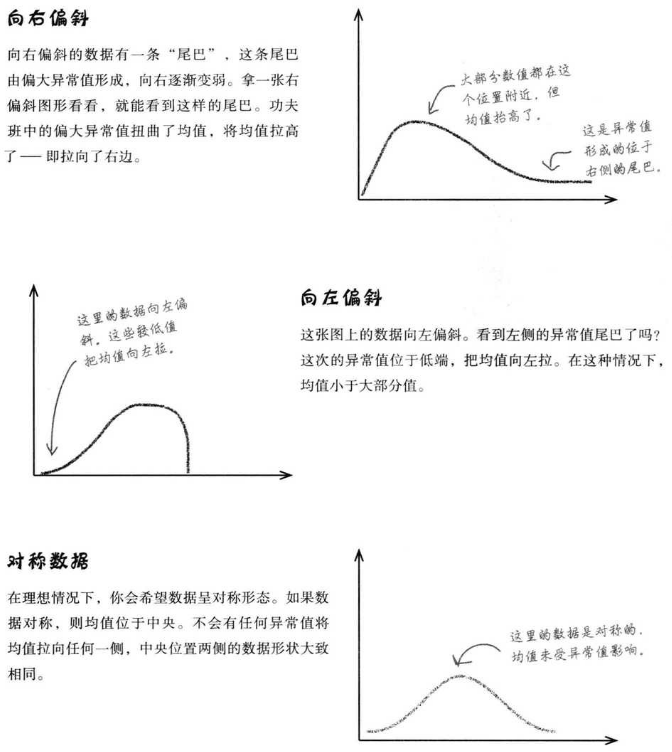
我们再看看这三张数据分布图，当异常值存在于右侧，平均值会被拉高；当异常值存在于左侧，平均值会被拉低；当数据呈对称心态，均值会位于中央。

中位数

当偏斜数据和异常值使均值产生误导时，我们可以采用其他方式表示典型值，比如中位数。中位数，通俗来说就是数字中位于最中间的数。

比如19 19 20 20 20 21 21 100 102的中位数是20。

下面给出求中位数的通俗办法：

• 把数字从小到大排列
• 如果有奇数个数字，n个数，中间数的位置为(n+1)/2
• 如果有偶数个数字，n个数，中间数的位置为(n+1)/2的两侧，将两个数字相加除以2，就是中位数了

在上面的案例中，中位数比均值更合适。均值有一个缺点就是：它可能会给出一个不存在于数据集中区的数值。不过不能完全否定均值，均值的优势通常远胜于中位数，均值对于抽样数据来说更稳定。

众数

再给出一个情境：有一位青年人想要参加游泳班，恰好有一个均值和中位数都为17岁的班级。但是事与愿违，这个班级的年龄分布情况是这样的：（这里的频数图1-2表示1岁是因为在现实生活中，1岁多 统称 为1岁）

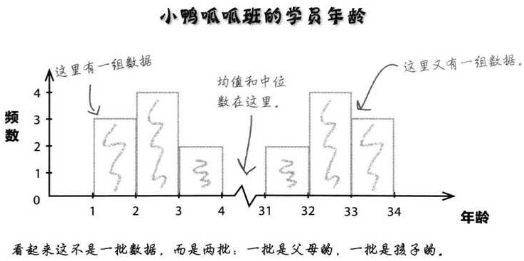
1 1 1 2 2 2 2 3 3 | 31 31 32 32 32 32 33 33 33

可以算出来，这个班级的年龄均值和中位数都是17。又或者我们多加一个孩子（例如3岁）/家长（例如31岁），中位数的年龄就会偏向为孩子（例如3岁）/家长（例如31岁）。

这个时候均值和中位数都失灵了。这时候需要众数出场。

众数，是一批数字中最常见的数值，即频数最大的值。众数可以不止一个。并且如果数据看上去体现了多种趋势或多批数据，那么我们可以为每一批数据给出一个众数。如果一批数据有两个众数，则我们说这种数据是双峰数据。

在上面的情景中，有孩子和家长两批数据，不存在某一个能完全代表整个班级的年龄，相反，我们可以看出每一批年龄的众数。在孩子组，2岁频率最高，在家长组，32岁频率最高，它们就是众数。

而且，众数还有另外一个功能。那就是它能用于类别数据。事实上，众数是唯一能用于类别数据的平均数。

当众数很多时，比如2个1、3个2、3个3、3个4，这时候众数就比较没用了。

求众数三步法：

1. 把数据中的不同类别或数值全部找出来
2. 写出每个数值或类别的频数
3. 挑出具有最高频数的一个或几个数值，得出众数

总结

以下是书上的总结：

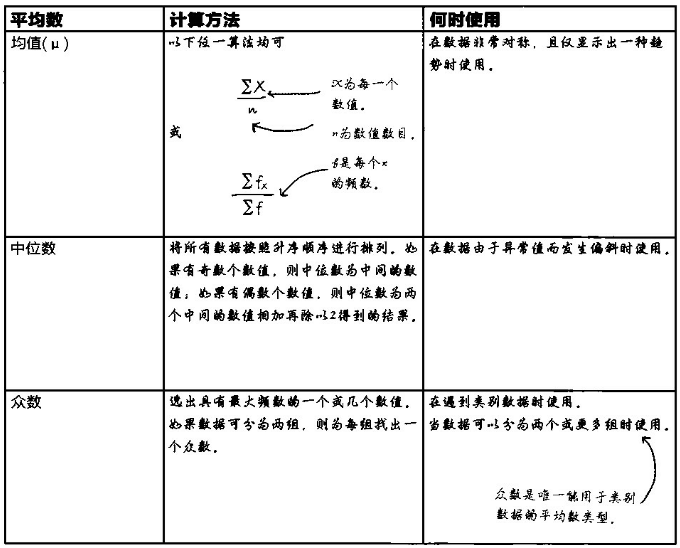
书上还有一个脑筋急转弯的题目，大家可以先不看答案思考一下再看看自己想的对不对：

开头的小故事

本地一家公司的员工由于感到自己拿到的薪水不公道，出现了不满情绪。大部分员工周薪为500美元，少数经理高一些，而首席执行官每周搞回家49000美元。

• 工人说平均薪水是每周2500美元，自己只有500美元，要求加薪
• 经理说平均薪水是每周1万美元，自己只有4000美元，也要求加薪
• 首席执行官说平均薪水就是每周500美元，我没有亏待谁，快回去干活吧

看看其中的“平均数”：

• 工人用的是中位数，这使得首席执行官的薪水造成的影响达到最低程度（可能是自己和经理比较工资觉得不满，或者是首席执行官只有仅仅几个人，工人使用中位数使得自己更有可能加薪【比均值低】）。
• 经理们用了均值，首席执行官的高薪令数据向右偏斜，均值因此显得虚高。
• 而首席执行官用了众数，大部分工人薪水就这么高。

实际上，每个人群都在使用最有利于自己意愿的平均数。统计量能够提供信息，但也能造成误导。在这个例子中，最适合的平均数是中位数，因为数据中存在异常值。