[因果推断] 什么是因果推断(一)_因果推理

一 什么是因果推断?

因果推理（Causal Inference）：Inferring the enfects of any treatment/policy/intervention/etc.
因果推理就是推断一个事物对另一个事物的影响。

关于因果关系，在《牛津哲学词典》的定义是，“当一个事件的出现导致、产生或决定了另一个事件的出现，这两个事件之间的关系就被称为因果关系。例如，外面正在下雨，不带雨具出门会被淋湿衣服。下雨和淋湿衣服之间就是因果关系， 下雨是原因，淋湿衣服是结果。

因果推断是统计学和数据科学的核心问题之一，在一种现象已经发生的情况下，推出因果关系结论的过程，就是因果推断。它在生物医学、经济管理和社会科学中有都有广泛应用，可以揭示变量之间的因果关系，发现现象背后的深层原因，比如：吸烟是否致癌？社会招聘是否存在性别歧视？也可以估计定量的因果效应，分析当原因改变时结果变量的响应，以帮助人们更科学的做决策干预，比如：教育水平如何影响一个人未来的收入？比如一种药物会使得病人生存期延长多少？等等。

因果推断也被认为是人工智能领域的一次范式革命，是近年来该领域的研究热点之一。未来，能否让AI像人一样思考？强人工智能是否能实现？为AI模型赋予因果关系思维似乎成了解答这些问题的必要因素和必经之路。

因果推断对科学来说是至关重要的，因为我们经常想提出因果要求，而不仅仅是关联性要求。例如，如果我们要在一种疾病的治疗方法中进行选择，我们希望选择能使大多数人得到治愈的治疗方法，同时又不会造成太多的不良副作用。如果我们想让一个强化学习算法获得最大的回报，我们希望它采取的行动能使它获得最大的回报。如果我们研究社交媒体对心理健康的影响，我们就会试图了解造成某一心理健康结果的主要原因是什么，并按照可归因于每个原因的结果的百分比排列这些原因。

因果推断对于严格的决策至关重要。 例如，假设我们正在考虑实施几种不同的政策来减少温室气体排放，但由于预算限制，我们必须只选择一种。 如果我们想最大限度地发挥作用，我们应该进行因果分析，以确定哪种政策将导致最大的减排。 再举一个例子，假设我们正在考虑采取几项干预措施来减少全球贫困。 我们想知道哪些政策将最大程度地减少贫困。

二 为什么研究因果推断?

当前的机器学习主要利用数据中的统计相关性进行建模。相关性的主要来源有：因果（causation）、混淆（confounding）、样本选择偏差（selection bias），三类分别对应以下三种结构：

 其中，只有由因果（causation）产生的相关，即因果关系，是一种稳定的机制，不随环境变化而变化；也只有这种稳定的结构是可解释的。例如，无论是在哪个国家，夏天时候天气变热（原因：T ），会导致冰淇淋的数量（结果：Y ）上升。

混淆（confounding）是指存在一个变量X ，该变量构成了T 和Y 的共同原因，如果忽略了X 的影响，那么T 和Y 之间存在假性相关关系：即T 并非产生Y 的直接原因。

样本选择偏差（selection bias）也会产生相关性。当两个相互独立的变量T 和Y 产生了一个共同结果变量S ，引入S 则为T 和Y 之间打开了一条通路，从而误以为T 和Y 之间存在关联关系。例如，有些非常勤奋的人去参加了就业培训，同时因为他们的勤奋得到了非常好的工作，此时，如果只考虑这部分勤奋的人群，那么在样本选择偏差的背景下，会产生参加就业培训帮助人们得到了更好的工作；而现实的情况可能是就业培训对找工作并没有什么帮助。

相关性 不等于 因果关系

"相关性 （Correlation）"经常被口语化地用作统计依赖性（statistical dependence）的同义词，然而，"关联 "在理论上只是对linear statistical dependence的一种衡量。在以后，我们将统一使用关联（association）一词来表示statistical dependence。

对于任何给定数量的关联，并不是 "所有的关联都是因果关系 "或 "没有任何关联是因果关系"。有可能存在大量的关联，而其中只有一部分是因果关系。"关联不等于因果 "只是意味着关联的数量和因果的数量可以是不同的。

例子一

如果我们在夏天时候发现游泳溺水的人数增加，如果忽略了气温的影响，仅凭冰淇淋销量与溺水人数呈现出来的正向相关关系，则可能得出吃冰淇淋会导致游泳溺水的错误结论。

例子二

假设我们有穿鞋睡觉和醒来后头痛的数据。结果发现，在大多数情况下，如果有人穿鞋睡觉，醒来后会头痛。而在大多数情况下，如果不穿鞋睡觉，醒来后不头痛。如果不考虑因果，人们把这样有关联的数据解释为“穿鞋睡觉会导致人们醒来头痛”，尤其是当他们在寻找一个理由来证明不穿鞋睡觉是合理的。

事实上，它们都是由一个共同的原因引起的：前一天晚上喝酒（喝醉了大概率才会穿鞋睡觉）。如图所示，这种变量被称为 "混杂因子（confounder） "或 "潜伏变量（lurking variable）"。我们将由confounder引起的关联称为confounding association，其实是一个虚假的关联 。

观察到的total association可以由混杂关联confounding association（图中红色箭头）和因果关联causal association（图中蓝色箭头）组成。可能的情况是，穿鞋睡觉确实对醒来后的头痛有一丢丢的因果关系。那么，总的关联将不只是混杂关联，也不只是因果关联，它将是两者的混合。例如，在图中，因果关系沿着从穿鞋睡觉到头痛醒来的蓝色箭头流动。而混杂关联则沿着从穿鞋睡觉到喝酒再到头痛的红色路径流动。

大量研究表明：过于依赖统计相关的建模方式，存在着严重的理论缺陷：缺乏因果关系考虑，仅从数据中学习到的相关性可能是错误的。首先，利用相关性学习的模型，泛化能力和稳定性差，极易受到场景变化或数据中异常值的影响；再者，过度依赖数据拟合的机器学习模型就像是一个黑盒子，缺乏可解释性。

随着人工智能的应用从互联网领域向工业、医疗、金融等领域的拓展，人工智能技术的优化方向也逐渐开始从「性能驱动」转向「风险敏感」。在这样的背景下，缺乏稳定性和可解释性极大地限制了AI模型的落地。在机器学习模型中加入因果机制，似乎已经成为弥补机器学习理论缺陷，进一步发展人工智能技术的必经道路。因果关系的稳定性和可解释性，强大到可以让人们有足够的信心去做科学且安全的决策，进而提高效率、降低成本、防止损失。

工业界和学术界存在大量使用因果推断改进人工智能模型的研究和应用案例。例如，在传统的网络营销中，为了研究网页上【了解更多】按钮还是【获取方案】按钮更促进转化，我们需要进行严格的控制实验，通过A/B测试去测量各个元素的转化效果。这种方法往往受到很多现实因素的限制，且成本昂贵。然而，我们可以通过在现有数据上使用因果推断来实现该目标。

三  什么意味着因果？

既然关联不意味着因果，那什么才意味着因果呢？

引入一个概念：potential outcomes（潜在结果）。看一个例子:

我现在头痛，我有一种药。如果我吃了药，头痛好了，那我就会得出结论，这种药对头痛有效。但如果我没吃药我的头痛也好了，我可能会认为，这种药对头痛无效。针对我吃药或是不吃药的情况，我的头痛好或是不好就是潜在结果。

 如上图，Yi​(1)代表吃药的潜在结果，Yi​(0)代表不吃药的潜在结果，那么吃药的因果效应就是潜在因果之间的差异。

但是现在有一个问题是，如果我吃了药，我可以观察到吃药的潜在结果 Yi​(1)，但我没法观察到不吃药的潜在结果 Yi​(0)，所以我没法计算因果效应。同样的，我不吃药的情况，没办法得到 Yi​(1)，也无法计算因果效应。

 

 原因是关联不意味着因果。我头痛是吃药的原因，所以会存在混杂关系，上式最右边的式子实际上是混淆关系和因果关系的混合。

为了去除混杂关系，可以做随机对照试验。对于一批人，为每个人随机地决定吃药或不吃药，观察他们的潜在结果。这样得到的潜在结果就不会有任何混杂因素的干扰，因为吃药或不吃药都是随机的。
 

四 怎么进行因果推断研究?

当前有关因果推断的研究主要包括两个方向：一是因果发现（Causal Discovery），二是因果效应的估计（Causal Effect Estimation）。因果发现旨在从纷繁的数据中，挖掘出变量之间的因果关系，其本质是要找到用于描述变量间因果关系的图网络结构。因果效应估计主要研究原因变量对结果变量的影响程度，其本质是建立因果模型并输出对增量的预测值。

以电商平台中对商品进行动态调价的应用为例。平台上商品价格往往不是一成不变的，需要随产品生命周期和市场需求波动等动态变化，准确的定价往往对于完成销售及盈利目标等具有关键意义。

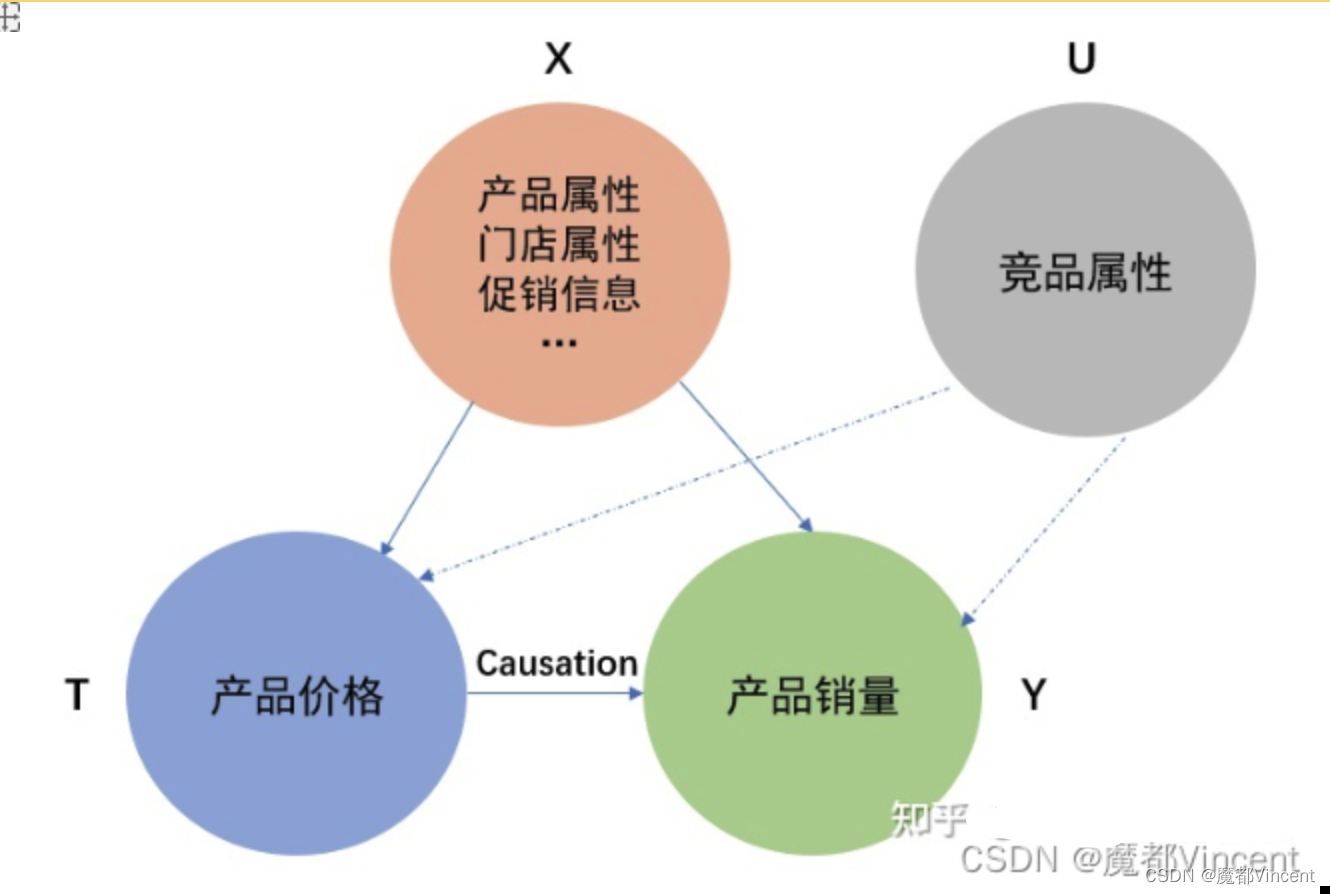
 基于因果发现方法，可以从大量产品属性、店铺属性、促销日、商品价格、商品销量数据中挖掘出它们内在的因果关系。通过构建一张完备的因果图，定性地刻画不同变量之间的作用关系，从数据中挖掘出的本质规律，会帮助提供合理的定价决策方向。

为了进一步研究商品价格与销量之间的关系，我们以因果图为指导，使用因果效应估计方法，定量地确定出每家店铺中每一种商品的价格对销量的影响程度，用于制定精准的价格调整策略。

在现实生活中，人们通过行为干预（Intervention）认知因果。以冰淇淋的销量为例，虽然我们不能直接干预天气变化，但是我们可以通过选择在干旱地区，即那些即使在夏天也无人游泳的区域，比较冬天和夏天冰淇淋的销量，得出冰淇淋的销量会随着气温上升而增加的结论；同样，我们可以选择比较干旱地区和湿润地区的冰淇淋销量，得知冰淇淋销量的增加与溺水人数并无因果关系。这样的行为干预，直接表现为控制实验（Controlled Experiment）。严格的控制实验，已经成为了研究因果关系的经典方法。然而，因果革命还带来了另一个重要成果，即允许我们在不实际实施控制实验的情况下，仅仅从观测数据中进行因果发现，并对因果效应进行估计。

观察研究中的因果

随机对照实验是得到因果关系的一种方法，但这种实验有时候会受到道德约束而不可行，有时候甚至不可能做这样的实验。因此观察研究是很重要的。在观察研究中，为了得到因果关系，需要调整或控制干扰因子。

 用W表示混杂因素，则在存在混杂关系的时候：

 通过对上式中的W进行边缘化（marginalize），就可以实现随机化T从而得到没有混杂因素的因果关系：

边缘概率（又称先验概率）是某个事件发生的概率。边缘概率是这样得到的：在联合概率中，把最终结果中那些不需要的事件通过合并成它们的全概率，而消去它们（对离散随机变量用求和得全概率，对连续随机变量用积分得全概率），这称为边缘化（marginalization）。

COVID-27的例子，可以用上面的公式计算因果效应了。下面只考虑Condition是Treatment的原因的情况。

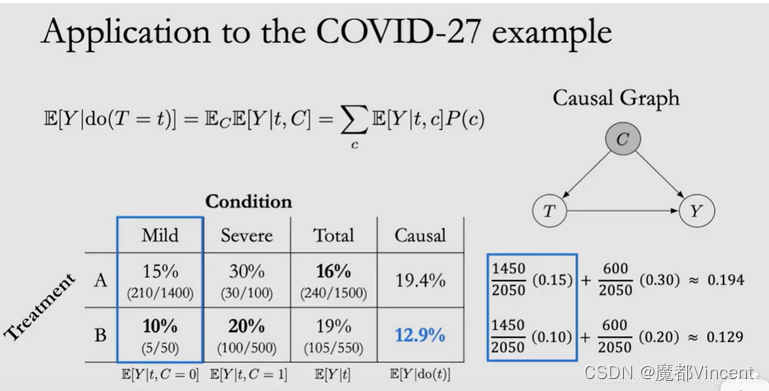
 由于这里的干扰因子W是C，而且是有两个取值的离散变量，因此可以将公式写为：

用这种计算方式，同种Conditon下A和B的权重相同，因此计算过程是公平的，不存在混淆因素的，计算结果可以看作因果关系的结果。

五 相关概念

Statistical vs. Causal 即使有无限量的数据，我们有时也无法计算一些因果量。 相比之下，许多统计数据都是关于解决有限样本中的不确定性。 当给定无限数据时，没有不确定性。 然而，关联是一个统计概念，并不是因果关系。 即使拥有无限数据，在因果推断方面还有更多工作要做。

Identification（识别） vs. Estimation（估计） 识别因果关系是因果推理的特有内容。即使我们有无限的数据，这也是一个有待解决的问题。然而，因果推理也与传统的统计学和机器学习有着共同的估计。

Interventional （干预）vs. Observational（观察）如果我们能够进行干预/实验，因果关系的识别就相对容易。这是因为我们可以实际采取我们想测量因果关系的行动，并简单地测量我们采取该行动后的因果关系。然而，如果只有观察性数据，识别因果关系比较困难，因为会有前面提到的confounder的存在。

因果推理学习笔记（一）_一千克欣喜的博客-CSDN博客

因果推断入门(1): 为什么需要因果推断 - 知乎 (zhihu.com)
灵魂三问：因果推断 - 知乎 (zhihu.com)