devbox
Gausst松鼠会
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

数据结构---设计---图论---有向无环图及其应用---【拓扑排序】_图论图序列实例

作者：Gausst松鼠会 | 2024-03-17 21:56:19

赞

踩

图论图序列实例

了解拓补排序前，我们先回顾离散数学中关于偏序和全序的定义：
若集合X上的关系R是自反的、反对称的和传递的，则称R是集合X上的偏序关系。
设R是集合X上的偏序(Partial Order)，如果对每个x，yEX必有xRy或yRx，则称R是集合X上的全序关系。
· 直观地看，偏序指集合中仅有部分成员之间可比较，而全序指集合中全体成员之间均可比较。

那么什么是拓扑排序(Topological Sort)?我们说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

我们知道，用顶点表示活动，用弧表示活动间的优先关系的有向图称作顶点表示活动的网，英文即Activity On Vertex Network ，简称AOV-网。
在这个网中，从顶点i到顶点j有一条有向路径，则i是j的前驱；j是i的后继。若<i,j>是网中的一条弧，那么i是j的直接前驱；j是i的直接后继。 可参考（b）来理解这句话。

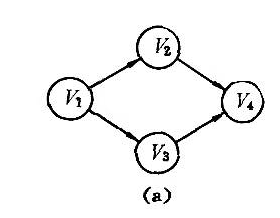
在这里插入图片描述
在这里插入图片描述

（a）表示偏序，(b)表示全序。若在(a)的有向图上人为地加一个表示v₂≤v₃。的弧（符号“≤”表示v₂领先于v₃)，则(a)表示的亦为全序，且这个全序称为拓扑有序(Topological Order)，而由偏序定义得到拓扑有序的操作便是拓扑排序。

AOV-网特点:
1.AOV-网中的弧表示活动之间存在的某种制约关系。
2.AOV-网中不能出现回路。

  • 典型AOV-网例题

对程序的数据流图来说，首先要判定所给定的AOV-网中是否存在环。检测方法就是对有向图构造其顶点的拓补有序序列，若网中所有的顶点都在他的拓扑有序序列中，则该AOV-网中必定不存在环，那么这样设计出来的流程图，工程可以正常进行。

先看简单的：

  • 某a专业学生必学课程AOV-网

在这里插入图片描述
基本思想：
（1）从AOV网中选择一个没有前驱的顶点并且输出;
（2）从AOV网中删去该顶点，并且删去所有以该顶点)为尾的弧;
（3）重复上述两步，直到全部顶点都被输出，或AOV-网中不存在没有前驱的顶点。
·拓扑排序后，有向图有如下两个拓扑有序序列：

拓扑序列：C1 , C2 , C3 , C4 , C5 , C6
拓扑序列：C1 , C2 , C3 , C4 , C5 , C6 ,C7

  • 设计数据结构：
    （1）.图的存储（利用邻接表存储，在顶点表中增加一个入度域in）
    在这里插入图片描述
    （2）.栈M（存储所有无前驱的顶点。也可以用队列。）
    步骤：扫描顶点表，将堆栈初始化。将入度为0的顶点B,E压入堆栈。
    弹出堆栈，取出栈顶元素E;根据顶点E的firstEdge遍历所有的边，将其所指向的各个顶点的入度值-1。
    在处理时，如果发现某个顶点的入度值为0，则压入堆栈。

  • 核心代码：

拓扑排序算法—伪代码

1.栈M初始化;累加器count初始化;
2.扫描顶点表，将没有前驱的顶点压栈;
3.当栈M非空时循环
3.1 Vj=退出栈顶元素;输出Vj;累加器加1;
3.2将顶点Vj的各个邻接点的入度减1;
3.3将新的入度为0的顶点入栈;
4.if (count<vertexNum)输出有回路信息;

void ALGraph::TopologicalSort(){
    for(int i=0;i<vertexNum;i++){   //in为0则压栈 
        if(adjList[i].in==0){
            s.push(adjList[i]);
        } 
    }
    while(!s.empty()){              //循环终止条件：栈为空 
        vertexNode v=s.top();       //弹栈输出 
        s.pop();
        cout<<v.vertex<<" ";
        count++;                    //计数加一 
        ArcNode *a=v.firstEdge;     
        while(a){                   //对弹出的结点遍历，所有遍历过的结点的in-1 
            adjList[a->adjvex].in--;
            int tmp=adjList[a->adjvex].in;
            if(tmp==0){             //如果某结点的in变为0，则将其压栈 
                s.push(adjList[a->adjvex])    ;    
            }
            a=a->next;
        }
    }
    if(count<vertexNum) cout<<"有环"<<endl; //如果计数小于顶点数则说明有环 
    else cout<<"无环，成功完成"<<endl; 
} 


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 完整代码
#include<iostream>
#include<stack>
#include<cstring>
#define MAX 100
using namespace std;
typedef struct ArcNode{         //边结点 
    int adjvex;                 //顶点下标 
    ArcNode *next;
}ArcNode;
typedef struct{
    int in;                     //in是入度 
    string vertex;              //顶点信息 
    ArcNode *firstEdge;             
}vertexNode,VertexNode[MAX];

class ALGraph{
    private:
        int vertexNum,arcNum;   //顶点数，边数 
        VertexNode adjList;     //顶点数组 
        stack<vertexNode> s;    //栈 
        int count=0;            //计数 
    public:
        ALGraph(string v[],int n,int e);
        void display();         //打印邻接表 
        void TopologicalSort(); //拓扑排序 
};
void ALGraph::TopologicalSort(){
    for(int i=0;i<vertexNum;i++){   //in为0则压栈 
        if(adjList[i].in==0){
            s.push(adjList[i]);
        } 
    }
    while(!s.empty()){              //循环终止条件：栈为空 
        vertexNode v=s.top();       //弹栈输出 
        s.pop();
        cout<<v.vertex<<" ";
        count++;                    //计数加一 
        ArcNode *a=v.firstEdge;     
        while(a){                   //对弹出的结点遍历，所有遍历过的结点的in-1 
            adjList[a->adjvex].in--;
            int tmp=adjList[a->adjvex].in;
            if(tmp==0){             //如果某结点的in变为0，则将其压栈 
                s.push(adjList[a->adjvex])    ;    
            }
            a=a->next;
        }
    }
    if(count<vertexNum) cout<<"有环"<<endl; //如果计数小于顶点数则说明有环 
    else cout<<"无环，成功完成"<<endl; 
} 
ALGraph::ALGraph(string v[],int n,int e){   //构造函数 
    vertexNum=n;
    arcNum=e;
    for(int i=0;i<vertexNum;i++){           //顶点初始化 
        adjList[i].in=0;
        adjList[i].vertex=v[i];           
        adjList[i].firstEdge=NULL;
    }
    ArcNode *s;
    int vi,vj;
    for(int i=0;i<arcNum;i++){
        s=new ArcNode;
        cout<<"请输入边的两个端点:"<<endl; 
        cin>>vi>>vj;
        s->adjvex=vj;
        s->next=adjList[vi].firstEdge;      //头插法 
        adjList[vi].firstEdge=s;
        adjList[vj].in++;                   //入度加一 
    }
} 
void ALGraph::display(){
　　 cout<<"in"<<" 邻接表"<<endl;
    for(int i=0;i<vertexNum;i++){ 
        ArcNode *p=adjList[i].firstEdge;
        cout<<adjList[i].in<<" ";
        cout<<adjList[i].vertex;
        if(p) cout<<"->";
        while
            p=p->next;
            if(p) cout<<"->";
        } 
        cout<<endl;
    } 
}
int main(){
    int n,e;
    cout<<"请输入顶点数和边数"<<endl;
    cin>>n>>e;
    cout<<"请输入结点信息"<<endl;
    string v[MAX];
    for(int i=0;i<n;i++){
        cin>>v[i];
    }
    ALGraph algraph(v,n,e);
    algraph.display();
    algraph.TopologicalSort();
    return 0;
}


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 输入

7 10 //顶点数和边数
C1 C2 C3 C4 C5 C6 C7 //顶点值
0 2
0 3
1 3
1 5
2 4
3 4
3 6
3 5
4 6
5 6 //输入边

  • 输出

in 邻接表
0 C1->C4 ->C3
0 C2->C6 ->C4
1 C3->C5
2 C4->C6 ->C7 ->C5
2 C5->C7
2 C6->C7
3 C7
C2 C1 C3 C4 C5 C6 C7 无环，成功完成
（答案可能不唯一）

拓扑排序：C1 , C2 , C3 , C4 , C5 , C6 ,C7

看了以上的简单示例，那么接下来增加编号

  • 某b专业学生必学课程AOV-网
    在这里插入图片描述
    在这里插入图片描述

基本思想：
由AOV网构造拓扑序列的拓扑排序算法主要是循环执行以下两步，直到不存在入度为0的顶点为止（说明有向图中存在环）。
(1) 选择一个入度为0的顶点并输出之；
(2) 从网中删除此顶点及所有出边。
可以参考第一道例题思想。

  • 核心代码

1.采用邻接表作有向图的存储结构，且在头结点中增加一个存放顶点入度的数组（indegree）；
2.入度为0的顶点即为没有前驱的顶点，删除顶点及以它为尾的弧的操作可以被以弧头顶点的入度减1来实现；
3.为了避免重复检测入度为零的顶点，可以再设一栈来暂存所有入度为零的顶点。

Status TopologicalSort(ALGraph G)(
//有向图G采用邻接表存储结构。
//若G无回路，则输出G的顶点的一个拓扑序列并返回OK，否则ERROR。
FindInDegree(G,indegree); //对各顶点求入度indegree[0..vernum-1]InitStack(S);
for(i=0;i<G.vexnum;++i) // 建零入度顶点栈 S
if(!indegree[i]) Push(S, i); // 入度为0者进栈
count = 0; // 对输出顶点计数
while(! StackEmpty(S))(
Pop(S, i);printf(i,G.vertices[i].data); ++ count; //输出i号顶点并计数
for(p=G.vertices[i].firstarc;P；p=p-＞nextarc)(
k=p-＞adjvex; //对1号顶点的每个邻接点的入度减1
if(!(—-indegree[k])) Push(S，k)；//若入度减为0，则入栈
)// for
)// while
if (count<G.vexnum) return ERROR; // 该有向图有回路
else return OK;
//TopologicalSort

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17

那后面大家就根据上面介绍的补充完整吧~

  • 参考完整代码<另一种方式>
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAXVEX 20
typedef char VerType;	//顶点值类型

struct EdgeNode{
	int adjvex;	//邻接点域，存储该顶点对应的下标
	int weight;	//用于存储权值，对于非网图可以不需要
	struct EdgeNode* next;	//下一个结点
};

struct VertexNode{
	int in;	//入度
	VerType data;	//值
	struct EdgeNode* firstedge;	//邻接表头指针
};

struct Graph{
	struct VertexNode vers[MAXVEX];
	int vernum, arcnum;	//顶点数和边数
};

/* 拓扑排序，若G没有回路，则输出拓扑排序序列并返回OK，若有回路返回ERROR */
int  TopologicalSort(struct Graph* G){
	struct EdgeNode* e;
	int i, k, gettop;
	int top = 0;	//栈指针下标
	int count = 0;	//统计输出顶点个数
	int* stack;	//存储入度为0的顶点
	stack = (int*)malloc(G->vernum * sizeof(int));

	for(i = 0;i<G->vernum;i++)	//遍历所有结点
		if(G->vers[i].in == 0)
			stack[++top] = i;	//将入度为0的顶点入栈

	while(top != 0){
		gettop = stack[top--];	//出栈
		printf("%c ",G->vers[gettop].data);
		count++;	//统计输出顶点数
		for(e=G->vers[gettop].firstedge; e; e = e->next){
			//弧表遍历
			k = e->adjvex;
			if(!(--G->vers[k].in))	//将k号顶点邻接点的入度减1
				stack[++top] = k;	//若为0则入栈，以便下次循环输出
		}
	}
	if(count < G->vernum)	//如果count小于顶点数，说明存在环
		return 0;
	else
		return 1;
}

/* 图初始化 */
void CreateGraph(struct Graph* G){
	int i, m, n;

	printf("输入顶点数和边数：\n");
	scanf("%d %d",&G->vernum, &G->arcnum);
	printf("输入顶点值：\n");
    getchar();	//吃掉回车
	for(i=0;i<G->vernum;i++){
		//getchar();	//吃掉回车
		G->vers[i].data=getchar();
		getchar();
		//scanf("%c",&G->vers[i].data);
	}
	//初始化图头结点指针和入度值
	for(i=0;i<G->vernum;i++){
		G->vers[i].firstedge = NULL;
		G->vers[i].in = 0;	//入度为0
	}
	printf("输入边：\n");
	for(i=0;i<G->vernum;i++){
		scanf("%d %d",&m, &n);
		struct EdgeNode *newNode = (struct EdgeNode*)malloc(sizeof(struct EdgeNode));
		newNode->next = G->vers[m].firstedge == NULL ? NULL : G->vers[m].firstedge;
		newNode->adjvex = n;
		G->vers[m].firstedge = newNode;
		G->vers[n].in++;	//入度+1
	}
}

int main(){

	struct Graph *G=(struct Graph*)malloc(sizeof(struct Graph)) ;
	CreateGraph(G);
	if(TopologicalSort(G)){
		printf("拓扑排序完成！\n");
	}else{
		printf("图存在环");
	}
	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Gausst松鼠会/article/detail/258228?site
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号