算法知识点总结：_算法转治

复杂度

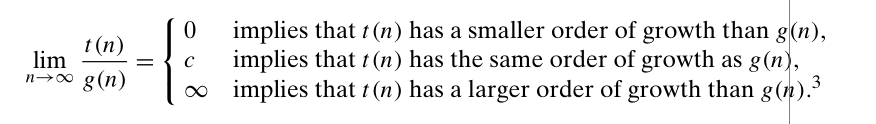
增长速率

$1<logn<\sqrt{n}<n<nlogn<n^2<2^n<n!$

运行时间

非递归算法复杂度计算步骤

• 决定一个或多个参数来指示输入的大小
• 确定算法的基本操作。(作为一个规则，它位于最内层的循环。)
• 检查基本操作的执行次数是否只取决于输入的大小。如果它还依赖于一些额外的属性，那么必须分别研究最坏情况、平均情况和(如果必要的话)最佳情况的效率。
• 建立一个表示算法基本操作执行次数的和
• 使用标准公式和求和操作规则，找到一个封闭的计数公式，或者，至少，建立它的增长顺序
  
  本题目中的 basic operation 应该是这个比较的句子，因为每一个 for 循环都会进行比较，而比较后的赋值操作却不是每次都要进行。

基本语句是 while 中的比较操作，因此，进行了 logn + 1 次，而不是 logn 次

排序算法

算法指标

选择排序（selection sort ）和冒泡（bubble sort）

复杂度
$\Theta (n^2)$

稳定性： 不稳定，举例 5 8 5 2，这样 2 和第一个 5 交换位置之后，就不稳定了
in-place 是原地排序算法

每次都从待排序列中选择最小的那个，交换到待排的位置。

冒泡排序

冒泡排序复杂度
$\Theta (n^2)$

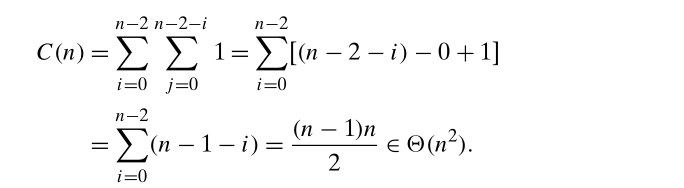
插入排序（insertion sort）

插入排序的基础思路是，将待插入的元素不断地和前一个进行比较，如果符合条件，就和前面的一个交换位置，从而实现最终把待排元素插入正确的位置，但是这样就无法避免多次冗余的 swap 行为，所以通过减治来解决这个问题。

• 这里的 basic operation 是 $A[j]>v$ 而不包含 $j>=0$
  复杂度： 最差为 $\Theta (n^2)$; 最好为：$\Theta (n)$
  稳定性： 插入排序是稳定的
  in-place： 是原地排序算法
  
  

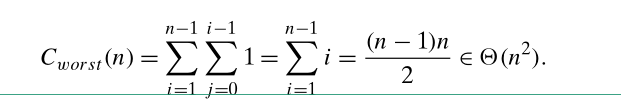
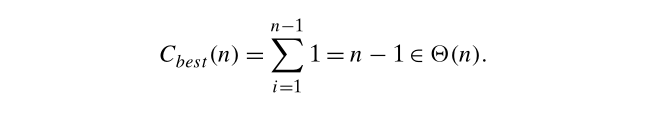
希尔排序（shell sort）

• 希尔排序是一种分段式的插入排序

归并排序（merge sort）

• 复杂度：$O(nlogn)$
  
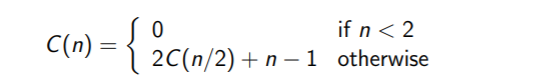
• 稳定性： 稳定
• in place： 不是原地的排序算法，空间复杂度 $O(n)$
  
  

快速排序（quick sort）

• 复杂度： 最坏 $O(n^2)$，最好：$O(nlogn)$
• **稳定性：**不稳定
• in-place： 是原地排序算法
  

堆排序（heap sort）

• **复杂度： **$O(nlogn)$
• 稳定性： 是稳定的排序算法
• in-place： 是原地排序算法
• 实施步骤：
  

暴力算法

顺序搜索算法（sequential search）

暴力字符串匹配

假设总字符串长度为 $n$ ，模板字符串长度为 $m$
总的比较次数最差的时候，外层循环 $i$ 需要挪动 $n-m+1$ 次，$i$ 每次 挪动的时候，内部的 $j$ 都要最多挪动 $m$ 次，因此总的复杂度为 $m(n-m+1)$

最近点（closest pairs）问题

• 复杂度：$\Theta (n^2)$
  

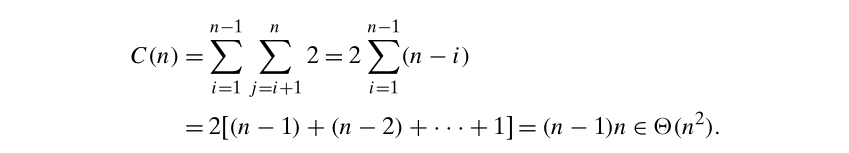
穷举搜索算法

问题类型

货郎问题

背包问题

分配问题

深度优先遍历

• 一般用 栈 进行演示
  
  

复杂度：

• 使用邻接矩阵进行 DFS 的复杂度是 $\Theta (V^2)$
• 使用邻接表进行 DFS 的复杂度是 $\Theta (|V|+|E|)$

使用 DFS 测试图的连通性

• 从一个点出发进行深度优先遍历，如果遍历完成之后，所有的点都被遍历过，那么证明这个图是连通图。
• 如果遍历完成之后，依然有点没有被遍历，那么证明图是不联通的。

使用 DFS 判断图中是否有环路存在

• 对于连通图来说，如果通过 DFS 遍历完成后存在 back edge，那么这个图是有环路存在的
• 对于非连通图来说，通过 DFS 遍历这个非连通图的每个连通部分，如果当前连通部分中出现了 back edge 那么就证明存在环路。

广度优先遍历

• 广度优先遍历思路：
  • 首先选定一个顶点
  • 逐个遍历与这个顶点直接相连的所有顶点
  • 逐个遍历与这个顶点相隔一个顶点的所有顶点
• 广度优先遍历一般使用 queue 来完成
• 相对于 DFS 的 back edge， BFS 有 cross edge
  
  

复杂度：

• 广度优先遍历使用邻接矩阵的复杂度也是 $\Theta (V^2)$
• 使用邻接表的复杂度是 $\Theta (|V|+|E|)$

图的深度优先遍历和广度优先遍历的总结

• DFS 基于“栈” ，BFS 基于队列
• DFS 有树结构和 back edge； BFS 有树结构和 cross edge
• 复杂度是一致的：当使用邻接矩阵的时候，$\Theta (V^2)$； 使用邻接表的复杂度是 $\Theta (|V|+|E|)$

哈希表

避免冲突的方法：

○ 链表法：

m 是 哈希表的 size， n 是存储的数据数量

• 下述描述了成功时需要消耗的 prob 的数量（探针查找数量）
  

○ 开放寻址法（open-addressing 法）=（closed hash 法）：

- 线性探测法：

- 双重哈希法：

Rehash

• 当负载因子 $\alpha >=0.9$ 的时候，进行 rehash
  

二叉树

二叉搜索树

• 左孩子小于父节点，右孩子大于父节点
• 缺点是：容易不平衡从而展成链式，影响查找效率

插入

• 比父节点大的插右边
• 比父节点小的插左边

插入复杂度：最坏为 $O(n)$，如果建立的是平衡的二叉树，那么插入的复杂度为 $O(logn)$

删除

被删除的节点包含四种情况

叶子节点

直接删除

只有左孩子

直接删除，左孩子节点替代当前的位置

只有右孩子

直接删除，右孩子节点代替当前的位置

左孩子有孩子都有

其实很好理解，看下面这个图

• 删除 60 这个节点，替代它的节点将会是 70 的最左孩子，但是 70 没有孩子，就用 70 来代替这个点，来保证整个树调整最小

二叉树

数据结构和抽象数据类型

数据结构：

数组，链表，队列，堆，栈，优先级队列，二叉树，图，集合

基本数据结构

• 数组
• 链表

抽象数据类型（结构）

除了基本的数据类型数组之外，其他的数据类型由于需要通过基本数据类型来实现，因此都是抽象的数据类型。

队列，堆，栈，优先级队列，二叉树，图

图

树

树是连通的无环图
图的边的数量 $E=V-1$

二叉树

二叉树的高度

• h 是 高度，n 是节点的总个数
  
  

二叉搜索树

平衡二叉树

减治算法

两种思路

• 自底向上 (bottom up)：可以视为一种增量算法，通常用递归的方式解决
• 自顶向下（top down）

通过一个常数实现减治（decrease by a constant）

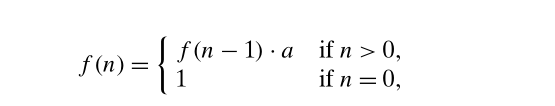
• 通过上面的算法可以得到这个问题的复杂度是 $O(n)$，因为采用上述递归式，每次子问题的规模缩小到原来的 $n-1$。但是如果采取下面的策略，整个问题的复杂度会收缩到 $O(logn)$
  

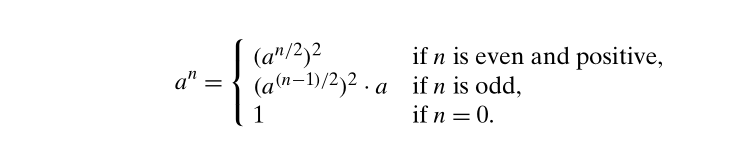
插入排序（insertion sort）

插入排序的基础思路是，将待插入的元素不断地和前一个进行比较，如果符合条件，就和前面的一个交换位置，从而实现最终把待排元素插入正确的位置，但是这样就无法避免多次冗余的 swap 行为，所以通过减治来解决这个问题。

• 这里的 basic operation 是 $A[j]>v$ 而不包含 $j>=0$
  复杂度：最差为 $\Theta (n^2)$; 最好为：$\Theta (n)$
  
  

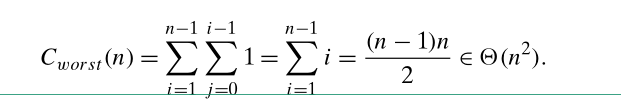
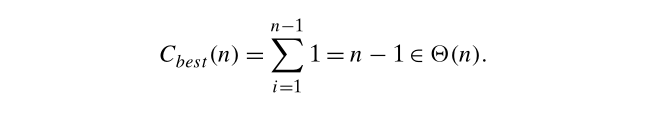
拓扑排序

• 只发生在有向图（directed graph）中

特别注意

拓扑排序有解的条件是，必须不能有环存在！！！即，绝对不能够出现 back edge

• 
  有的节点有前驱结点，有的没有前驱结点，必须按照顺序，不能出现 C3 出现 C1 或者 C2 前面的情况
  

节点的删除

拓扑排序的算法思路

• 统计所有节点的入度情况，记录在数组中
• 将所有入度为零的节点选出来，加入队列
• 当队列不为空的时候将节点弹出，弹出的节点为 $u$
• 遍历与弹出节点 $u$ 相连的边 $(u,w)\in E$，并把节点 $w$ 的入度减 $1$；如果 $w$ 的入度减为 $0$ 则也将 $w$ 加入队列

Example：

通过常数因子实现减治（decrease by a constant factor）

Binary Search (二分查找)

复杂度：$O(lo{g}_{2}n)$
最坏情况下：



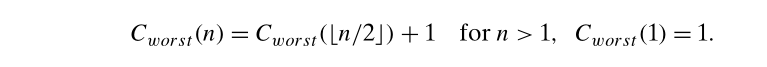
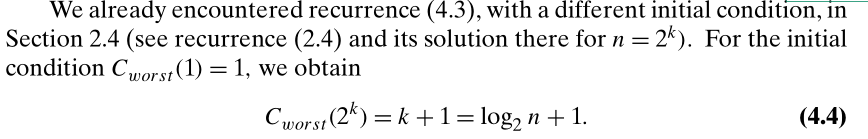
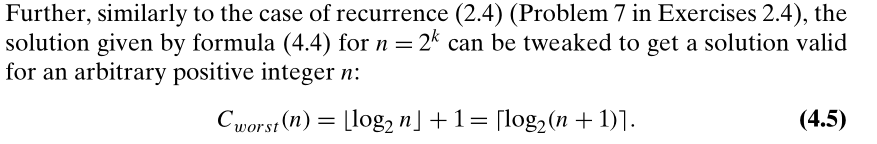
所以对于一个正整数，最多比较的次数上限就是 $lo{g}_2(n+1)$ 次

Lumuto 分区算法

快速选择算法 （kth smallest element）

复杂度： $O(nlogn)$

• 当我们的算法完成 分区之后，$s$ 的位置前面都是比他小的数字（索引是从 0 开始，所以 $s$ 位置上是第 $s-lo+1$ 小的数）所以如果 k 刚好是第 $s-lo+1$ 小的数，那么直接就返回 $s$ 位置上的数。这就是为什么判断的条件是 $s-lo=k-1$
• 如果 $s-lo+1>k$，比如 $s$ 的位置是第 $5$ 小的数，那么这个时候，$s-lo+1>k$ 证明 $k$ 只能是 第 $4$ 小或者第 $3$ 小。。。因此应该往左边找。
• 反之，应该往右边找，只是相对于右边的数字来说，原来的第 k 小要变成第 $(k-(s-lo+1))$小，即 $k-s+lo-1$ 小

插入查找法

• 直接套公式求解
• 复杂度：$O(loglogn)$
  

缩小变量规模（variable size decrease）

分治算法

主定理（master theorem）

归并排序（merge sort）

• 复杂度：$O(nlogn)$
• 
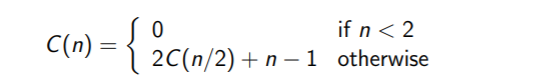
• 稳定性：稳定
• in place：不是原地的排序算法
  
  

快速排序（quick sort）

• 复杂度：最坏 $O(n^2)$，最好：$O(nlogn)$
• 不稳定，in-place
  

Hoare 分区（Hoare Partitioning）

• 适合 Lumuto 类似的分区算法
• 复杂度：$O(lnogn)$
  

Median-of-three

树的遍历（tree traversal）

前序遍历（pre-order）

中序（in-order）

后序（post-order）

使用栈来完成 pre-order 遍历

• 其实对树的前序、中序、后序遍历都和图的深度遍历相似，因此可以使用 stack 来实现
  

○ 未解决：如何使用栈实现其他顺序的遍历

层序遍历（level-order）

最近点问题改进（closest pair）

堆、优先级队列、堆排序

堆的性质

• 堆是一种局部排序的二叉数
• 必须是完全二叉树（而且必须满足从左往右，从上到下依次添加元素）
  

自底向上建堆（bottom-up）

建堆复杂度：linear-time（$O(n)$）

○ （有问题）弹出操作（Heap Eject）

为什么不交换完之后直接把 9 弹出，而要最后再弹出 9

• 交换堆顶和堆底的元素，
• 将当前栈顶元素按照 sift down 的原则下降到新的位置 （只考虑下图 9 之前的元素的重新排列问题）
• 弹出当前栈底元素（即开始的栈顶元素）
  

优先级队列（priority queue）

优先级队列的相关操作：

• 优先级队列的应用：
  
• 操作的复杂度：
  • 入队（inject）：$O(logn)$
  • 出队（eject）: $O(logn)$

堆排序（heap sort）

• 复杂度：$O(nlogn)$
• in-place 但是不稳定
• 实施步骤：
  

转治算法（Transform-and-conquer）

原则

使用排序作为预处理的转治算法

唯一性检查

• 检查整个序列中是否存在相同的值。
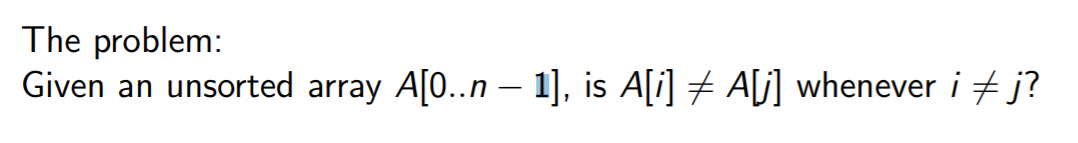  如果直接使用暴力法，复杂度是 $O(n^2)$
  
• 如果采用转治算法，先进行排序，那么相同大小的数都会靠在一起，因此只需要检查相邻位置即可，复杂度为 $O(nlogn)$
  

模式查找（mode finding）

• 变位词
  

平衡树

AVL树

• 插入和删除的复杂度都是 $O(logn)$
  左旋和右旋 先从最先插入的节点开始调整平衡状态。如下图，数字 3 所在的节点之所以不平衡是因为插入了数字 “1”，进而才导致 “4” 也不平衡了，所以根本解决在于解决 3 节点的不平衡。因此要对 3 进行右旋操作
  
  双旋转情况
  

2-3树

2-3 树存在两种节点：

• 二节点：一个节点里面有一个值，只能有 0 个或者 2 个子节点
• 三节点：一个节点里面有两个值，只能有 0 个或者 3 个子节点
• 一个节点称为 n 节点，是因为它最多有 n 个子节点而不是他一个节点里面有 n 个值
  
  
• 完全步骤： 在整个过程中产生的三节点的个数一共是 4 个，分别是 （5,9），（3,5），（3,8），（4,5）
  

2-3树高度

空间换时间（space / time trade off）

• 很多时候我们进行递归算法，会有大量重复运算的步骤，拿斐波那契数列来说，如果我们使用递归实现，那么他的递归树如下图所示；图中红框的部分都是进行反复计算的冗余计算。如果我们能够把每个递归的结果先记录下来，那么我们在进行第一个 Fib(n-2)是返回的运算结果存储在表中，下一次我们进行 Fib(n-2) 的时候就可以先进行查表得到它的结果，就可以避免大量重复的计算。
• 这个时候我们采用 bottom-up 自下而上建立表格的思维。所谓的 bottom 就是较低次序的数，比如 Fib(1) 相对于 Fib(n) 就是 bottom

斐波那契数列

• 这里我们事先安排了一个表格，表格的每个位置初始化为 0 ，让每一步计算的值都存放到表格里面

计数排序

复杂度： 线性复杂度，因为不需要进行 comparison。
适用情况： 序列中重复的值很多，不重复的值很少且范围较小。

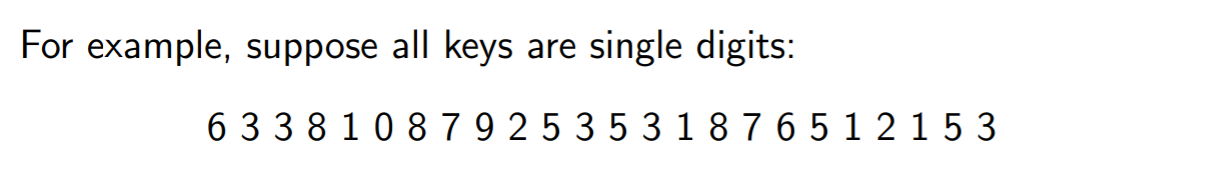
这种情况下我们可以：

• 扫描一遍待排序列，然后统计每个数字的个数
• 按照顺序把每个数字按照他们的个数进行排列
  
• 第二个表是如下方式得到的，最终确定的是不同元素所处的位置区间。
  

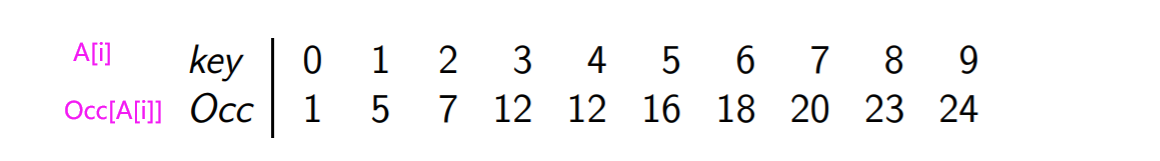
Horspool’s String Search

• 初始化查找表格
  
  
  
  算法步骤大概如下：
• 把要步进的表格先做出来，上面这种情况的表格应该是
  
• 让 $i$ 初始化为第一次比较的 $pattern$ 的尾部，从尾部开始比较，一直到 $i=n-1$ 代表序列比较完成
• $k$ 是负责内部循环的，每次 $i$ 确定了位置，就是用 $k$ 来完成逐位比较，$k$ 也是从后往前比较的；
• 如果在 $k$ 挪动过整个 $pattern$ 长度的过程中，所有的位置都匹配，那么就返回 $i-m+1$ 其实就是 $i-(m-1)$ 即当前 $pattern$ 头部的位置
• 如果 $k$ 在挪动的过程中发现有位置不匹配，那么直接查表往后跳 $Shift[T[i]]$ 个位置，直到整个过程结束。

哨兵法改进 Horspool’s String Search

• 首先把 T 数组后面添加一个完整的 pattern，上面的例子就会变成下图：
  
• 这样的好处就是，再也不用考虑数组下标越界的情况，而只专注于是否匹配，当 i > n 的时候，自然就停止了。
  

Horspool’s String Search 的复杂度

动态规划

应用场景

• 解决递归式的问题
• 解决递归中存在大量重复的递归步骤的时候
• 动态规划问题是基于上面的 “空间换时间” 的思维，避免重复的计算，采用的也是 bottom-up 建立表格的方法
• 解决一些优化问题
  

取硬币问题

• 设定 n 个硬币的值分别为 $v_1,v_2,...,v_n$
• 用 $S(i),i\in 1,...,n$ 表示在第 $i$ 步能够取到的最大的和
• 因此我们可以知道 S ( i ) = M A X { S ( i − 1 ) , S ( i − 2 ) + v i } S(i)=MAX\{S(i-1),S(i-2)+v_i\} S(i)=MAX{S(i−1),S(i−2)+vi​}；这个式子代表了，在第 i 步能够获得的最大的和是产生于两种不同的选择：
  • 一是选择了当前的 $v_i$ , $S(i-2)+v_i$ 就会代表本步骤的和值
  • 二是没有选择当前的 $v_i$, $S(i-1)$ 就会继续成为本步骤的和值
• 初始化表格：因为递归式里面涉及到 $S(i-2)$ 和 $S(i-1)$，所以我们要保证最初的表格有值，因此我们需要初始化前两个的值：
  

注意事项

• 几乎在所有的动态规划题目算法中，都会空出数组下标 0 的位置，从 1 开始，例如 $Fib(1...n)$, $S(1...n)$

○ 将被选择的硬币的位置保留下来

背包问题

• 一共有 $n$ 个物品，重量分别为 $w_1,w_2,.....,w_n$，价值分别为 $v_1,v_2,...v_n$ 背包的容量为 $W$

• 这道题的关键是要找出递归关系，如何建立在 $v$ 和 $w$ 之上的递归关系

• 让我们先回顾一下选硬币的思路：
  S ( i ) = M A X { S ( i − 1 ) , S ( i − 2 ) + v i } S(i)=MAX\{S(i−1),S(i−2)+v_i\} S(i)=MAX{S(i−1),S(i−2)+vi​}
  这个思路就是分为了针对第 $i$ 个硬币的时候，选还是不选。
  同样地，当我们把一对物品排成一行，挨个问你选不选的时候，就变成了类似的问题。好，让我们切换一下情景。一共 $i$ 个物品摆在这里
  

• 我们用 $S(i)$ 表示对于第 $i$ 个物品做出最好选择之后得到的价值

• 从第 $i$ 个开始考虑写递归式，假设我取了第 $i$ 个物品，$S(i)=S(i-1)+v_i$，如果不取第 $i$ 个，那么 $S(i)=S(i-1)$ 到这个地方为止似乎没毛病，但是出现了一个问题，那就是：相对于选硬币问题，背包问题是个两维度的问题，就是说它的选择 既涉及到价值，又涉及到重量。因此，重量也应该是我们考虑的一个因素，那么怎么把重量因素加入现有的递归式呢？

• 因此我们在构造递归式的时候这么考虑，当我正面对第 $i$ 个元素犹豫不决的时候，我的目标只有一个那就是使整个包就会在当前重量限制下达到最大的价值，用 $S(i,W)$ 来表示这个目标、因此，我们现在把原递归式扩展成：

• 假设我面对第 $i$ 个物品，我取了它，接下来我要面对的物品是$1,2,...,i-1$，而整个包的重量限制会变成$W-w_i$，因此当我取了第 $i$ 个物品，$S(i,W)=S(i-1,W-w_i)+v_i$，而如果我不取它，那么下一步的重量限制还是 $W$，因此为 $S(i,W)=S(i-1,W)$

• 结合取第 $i$ 个物品和不取，递归式应该类似于选硬币问题：

  S ( i , W ) = m a x { S ( i − 1 , W − w i ) + v i , S ( i − 1 , W ) } S(i,W)=max\{S(i-1,W-w_i)+v_i,S(i-1,W)\} S(i,W)=max{S(i−1,W−wi​)+vi​,S(i−1,W)}

• 当然还有一点需要考虑，也是背包问题较为复杂的原因，那就是，当我们面对第 i 个物品的时候，如果他本身的重量就比当前的背包重量限制还要大，即 $W<w_i$ 那我们没有办法，直接不能选择这个物品，所以这种情况下 $S(i,W)=S(i-1,W)$。

• 综上所述，整个背包问题可以被用如下的递归式进行表示：
  
  
  

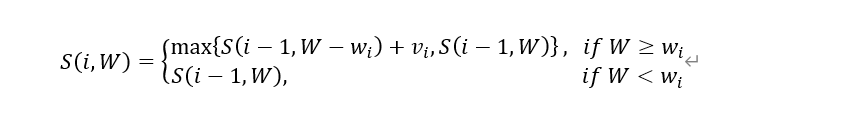
hash 表实现背包问题

有向图闭包传递算法（transitive closure）：Warshall’s Algorithm

闭包传递问题的定义

• 在交际网络中，给定若干个元素和若干对二元关系，且这些关系具有传递性，通过这些传递性推导出尽量多的元素之间的关系的问题叫做传递闭包。
• 也就是说，在一个元素集里，对你说一堆：某两个元素之间有关系。然后问你这些元素中一共有多少个元素有关系
• 传递闭包概念的重点就是，这个关系必须是二元的，也就是说，其他的多元关系也一定要可以分解为几个二元关系的累积

Warshall 算法思路

• 初始化表格，对于所有的点，判断能够到达其他的点，能到达的标 1 ，不直接到达的标 0
• 当第一个点作为 stepping-stone 的时候，判断剩余的所有点可以借助第一个点去哪里，能到达的更新为 1，不能到达的不更新
• 当第二个点作为 stepping-stone 的时候，同样判断其他的点。。。循环往复一直遍历完所有的点
• 整个算法有三重循环，第一重是把所有的点都挨个当做 stepping-stone，剩下两重则是在 stepping-stone 确定的条件下遍历整个表格，进行数据更新

复杂度： $O(n^3)$

有向带权图中的最短路径问题（shortest distances）: Floyd’s Algorithm

• 解决了所有顶点之间的最短路径问题，即可以找到 每个点到其他另外的点分别的最短距离
• 这里区别于 Dijkstra 算法，他只能找到 “固定一个点，这个点到其他点分别的最短距离”
• 图中的权值都需要为正值
• 有向图无向图都可以使用这种算法
• 不直接连接的顶点，距离初始化都为 $\infty$
  

Floyd 算法思路

• 初始化表格，对于每一个点，能直接到达的点初始化为这条边的权值，不能到达的初始化为 $\infty$
• 把每一个点分别当做 stepping-stone，更新其他的点能通过当前的 stepping-stone 去的新的点，更新值的过程分为下面步骤:
  • 若被更新的位置是正无穷，则直接更新
  • 若被更新的位置是一个常数，更新的时候要判断即将更新的值小于现在的值。
    
    

贪婪算法

• 贪婪算法的思路是不断寻找局部最优解，
• 贪婪算法不一定能找到全局最优解

普利姆算法（Prim）寻找最小生成树

生成树和最小生成树

生成树

• 因为生成树首先是一棵树，所以他的内部不能有环路
  
  最小生成树
• 各边之和最小的生成树
  
  

普利姆算法思路

• 初始化一个顶点集合 $V_T$，这个集合代表着我们最终用来构造最小生成树的点集，最开始拿一个点放进去
• 初始化一个边集合 $E_T$，用来存放最小生成树生成过程中产生的边
• 对剩下的 $|V|-1$ 个点进行遍历，找到他们离 $V_T$ 中的点的最小距离的顶点，把这个顶点加入 $V_T$，这条最短的边加入 $E_T$
• 返回整个 $E_T$ 集合
  

• 那如何找到距离当前步骤的 $V_T$ 集合最小的点呢？通过最小堆构建优先级队列来不断地完成这个任务。
• 下面的算法思路如下：
  • 首先把所有的点分为已经加入最终解的点和暂时没有加入最终解的点，最开始，只有 $v_0$ 加入最终的解；

• 在表示的时候因为 $cost$ 和 $pre$ 都是为顶点服务的列表，因此我们在表示的时候可以用 $V(c,p)$ 来表示当前节点的状态，方便可视化步骤，例如当前 $u=a(0,nil)$ 代表当前的节点是 $a$，他到最近的前驱结点的 $cost$ 是 0，前驱结点是 $nil$
  
• 当然也可以用这个表格来看，本质是一样的
  

算法复杂度

• 用邻接矩阵 $O(|V|\cdot |E|)$
• 使用邻接表 $O(|E|log|V|)$
  

迪杰斯塔拉（Dijkstra）

前驱问题：Floyd 算法

• 弗洛伊德算法也是找最短路径问题，但是复杂度是 $O(|V{|}^3)$
  

Dijkstra 算法的特点

• 有向图和无向图都适用

• 迪杰斯特拉算法不能用于存在负数边的情况。否则会出现下面情况
  

• 用于找到从一个 固定的起始点 开始到 其他所有点 分别的最短距离，即 单源的最短距离问题。

• 区别于 Floyd 算法：Floyd 可以找到 每个点到其他另外的点分别的最短距离
  

Dijkstra 算法思路

• 迪杰斯特拉算法的思路和普利姆类似，当确定了起始点 $a$ 之后，把节点分类为两类，一类是已经确定了到 $a$ 点最小距离，这类点用 $V_T$ 表示，其他点用 $V_R$ 表示。每次从 $V_R$ 中选出距离前驱结