PatchMatch分析_金字塔 patchmatch

1.介绍

　　作为纹理合成的方法，PatchMatch利用图片中的其他区域来恢复边缘区域，想法很合理。并且在实现上巧妙的利用了offset这样一个信息，使得计算上也不算复杂。此为Barnes et al 的得意之作，去年他在我方圆3米的距离坐了2个月都没和他交流，真是暴殄良机，心塞。人总是失去了才知道珍惜- -。

1.1块（Patch）

　　图像一片正方形的区域，如3x3,5x5,此为PatchMatch算法的最小操作单位。作为一个块，其比单个像素所包含的信息更多，因此更好用。

1.2图像重组（Reshuffle）

　　Reshuffle即将一张图片进行重新组合，如将图片右上角的塔贴到左边，并且使得看起来很自然。

　　　　　　　　　图一 　　　　　　　　　　　　　　　　　　　　图二
　　图1中可以看到塔的边缘有很明显的边界，为了消除边界，需要进行边缘的融合等操作来完成，一般方法有解泊松方程。PatchMatch中的reshuffle并不解方程，而是找到边缘部分与图片其他部分最匹配的（match）区域，利用此区域来填补边界，达到自然的效果，结果图2.

2.算法

　　我们需要得到的是target图片中每个区域在src图片所最匹配的区域记录在offsetmap中，即patchmatch的输出结果即为一张offset的映射。

　　　　　　　　src图片　　　　　　　　　　　　　　　　　　　target图片

2.1初始化offsetmap

barnes在随机初始化的基础上加上了2个trick：
1、将边界区域的offsetmap值都初始化为0，这样一般而言这些位置都很难被更改所以一开始就是对的，那么在propagation的时候就很容易向后面蔓延。
2、将被覆盖的区域的偏移量指向其原来的地方，这是一个事实，因为原来的地方和这里要变成的地方是同样一个东西。然后通过constraints来防止后面的ANN将其修改。如下图

最后初始化的Offsetmap如图，可以看到边界是黑的，即其对应的match坐标就是它自己的坐标：

2.2最近邻搜索（Ann）

　　对于target图片中每一个patch，都要在src图片中找到最匹配的patch，Ann最后的输出就是一张记录对应位置的偏移矩阵（offsetmap，2维），由于2张图片的大小是一样的，所以只需要记录PatchA离对应PatchB的偏移量即可。
PatchMatch最近邻算法的思想精妙在于其利用了如果在src中找到与target的PatchB相匹配的PatchA，那么PatchB周围的区域也很可能与PatchA周围的区域相匹配，即图像的局部相关性，就不用全局搜索了。而其实现的精妙就是利用了偏移量，如下图

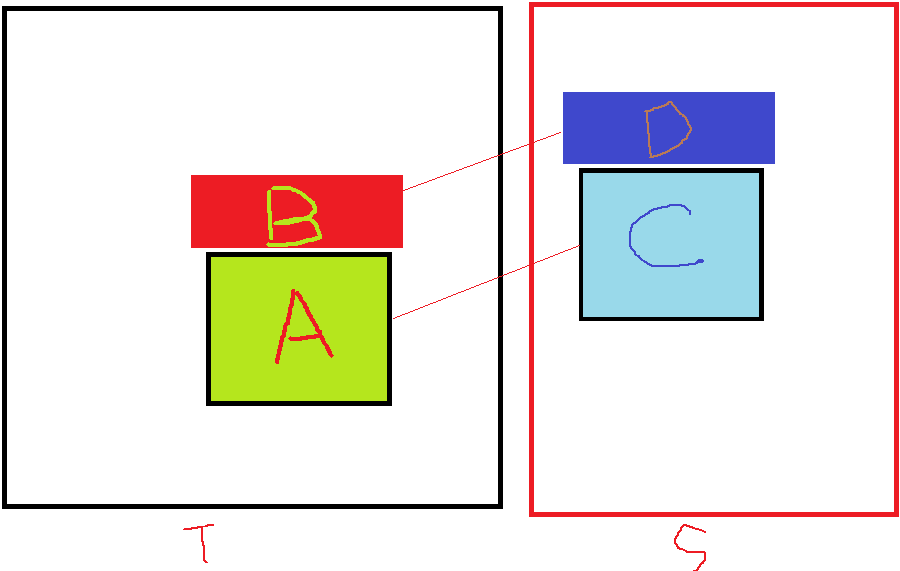
在target图片中如果找到了PatchB的对应块PatchD，那么PatchA的对应块就很可能是PatchC。

随机搜索主要分2部分：propagation和random search

2.2.1propagation（顺序蔓延）：

　　算法在偶数次对一个Patch查找其原对应点左(x-1,y)上(x,y-1)的Patch，奇数次查找右(x+1,y)下(x,y+1)。如上图是偶数次，假设开始的时候Target中红色Patch（x，y）所对应为Source的红色Patch（offmap（x，y），这个值可能是初始化有的也可能是后面更新过的），由于其左边黑色的Patch（x-1，y）对应的是黑色（offmap（x-1，y）），所以我们认为绿色和红色匹配的概率更大，需要进行比较。而且如果说确实Source图中绿色比红色更匹配target图中的红色Patch，那么offmap（x，y）就等于offmap（x-1，y），并不是offmap（x-1，y）[x] + 1！因为是偏移量，不是具体位置

2.2.2random search（随机扰动搜索）：

　　为了保证能够更快的找到offmap，需要给上面的顺序模式加个扰动以使得搜索空间更大。如下图，这一步骤是每对一个Patch进行顺序步骤后就进行一次。

　　这个随机扰动的方式是在自己为中心的某个大小矩形框内搜索，其中搜索框大小公式为：
　　　　　　　　　　　　　　　　　　　　
　　R是一个随机值（-1-1之间），w是搜索框初始大小，a是缩小系数，V0为初始的Patch位置，随着i的增加，搜索框实际大小waR将减小直至小于1则停止搜索。a一般为0.5.

ps：以上所有步骤都不会对constrants区域进行修改，因为在初始化的时候就已经确定其offset的值。

2.３Reshuffle

　　通过得到了offsetmap之后我们就可直接通过这个位移关系将新的图片通过“贴图”的方式将其生成。在纹理合成中一般会使用图像金字塔在不同的尺度进行合成，这样可以利用到不同尺度的信息从而使得融合效果更好，比如经过下采样之后图片一个Patch可能就包含整个物体，而在搞分辨率的图片上一个Patch可能就是一点点细节，那么我们在低分辨率的图片上就可以先找到大的物体的对应，然后将信息向上传递，就可以不断在高的分辨率的图片上找匹配而使得细节更好。下图为总体框架：


具体实现由2个问题：
1、在开始的时候如何创建第一张图片。
2、得到低分辨率的图片和offsetmap之后如何向上传递信息。
3、文章中的EM是怎么反映的。

第一个问题：我们有offsetmap，而且那张图片在复制的区域内的偏移是指向正确的位置的，那么在经过迭代后的offsetmap我们直接拿来贴图就可以得到第一张图片，而且由于分辨率较低，即使边界部分的offset匹配不对，在图片上我们也根本看不出来。
30*40 res：

60*80 res:

160*120 res:

第二个问题：这个信息通过offsetmap的插值来进行传递：

/给constrans和offsetmap上采样
void PyrUpOffsConst(Mat InO, Mat InC, Mat &OutO, Mat &OutC) {
    int rows = InO.rows * 2;
    int cols = InO.cols * 2;
    OutO = Mat(rows, cols, InO.type());
    OutC = Mat(rows, cols, InC.type());
    int m = 0, n = 0;
    while (m<InO.rows) {
        int m2 = m * 2;
        n = 0;
        while (n<InO.cols) {
            int n2 = n * 2;
            OutC.at<uchar>(m2, n2) = InC.at<uchar>(m, n);
            OutC.at<uchar>(m2 + 1, n2) = InC.at<uchar>(m, n);
            OutC.at<uchar>(m2, n2 + 1) = InC.at<uchar>(m, n);
            OutC.at<uchar>(m2 + 1, n2 + 1) = InC.at<uchar>(m, n);
            OutO.at<Vec2f>(m2, n2)[0] = InO.at<Vec2f>(m, n)[0] * 2;
            OutO.at<Vec2f>(m2, n2)[1] = InO.at<Vec2f>(m, n)[1] * 2;
            OutO.at<Vec2f>(m2 + 1, n2)[0] = InO.at<Vec2f>(m, n)[0] * 2;
            OutO.at<Vec2f>(m2 + 1, n2)[1] = InO.at<Vec2f>(m, n)[1] * 2;
            OutO.at<Vec2f>(m2, n2 + 1)[0] = InO.at<Vec2f>(m, n)[0] * 2;
            OutO.at<Vec2f>(m2, n2 + 1)[1] = InO.at<Vec2f>(m, n)[1] * 2;
            OutO.at<Vec2f>(m2 + 1, n2 + 1)[0] = InO.at<Vec2f>(m, n)[0] * 2;
            OutO.at<Vec2f>(m2 + 1, n2 + 1)[1] = InO.at<Vec2f>(m, n)[1] * 2;

            n++;
        }
        m++;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

第三个问题：EM算法是如何实现的，下面代码反映了这个算法

    while (i > 0)
    {
        fprintf(stdout, "PyrUp Step %d\n", i);
        for (int j = 0; j < EMiter; j++)
        {
            for (int k = 0; k < Anniter; k++)
                func.EStep(offs[i], srcset[i], dstset[i], cons[i],patchsize, k, i * searchwindow);
            generateimg(srcset[i], dstset[i], offs[i], patchsize);
        }
        PyrUpOffsConst(offs[i], cons[i], offs[i - 1], cons[i - 1]);
        generateimg(srcset[i - 1], dstset[i - 1], offs[i - 1], patchsize);
        i--;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13

EM算法：
最大期望算法经过两个步骤交替进行计算：
第一步是计算期望（E），利用对隐藏变量的现有估计值，计算其最大似然估计值；
第二步是最大化（M），最大化在 E 步上求得的最大似然值来计算参数的值。
M 步上找到的参数估计值被用于下一个 E 步计算中，这个过程不断交替进行。

有些程序还是要自己写一遍才知道好多细节啊- -。

3.参考资料

1、Patchmatch: Image reshuffling

http://cybertron.cg.tu-berlin.de/pdci11/PatchMatch/

2、Image reshuffling with PatchMatch

http://cybertron.cg.tu-berlin.de/pdci11ws/patchmatch/index.html

3、PatchMatch: A Randomized Correspondence Algorithm for Structural Image Editing

http://gfx.cs.princeton.edu/pubs/Barnes_2009_PAR/