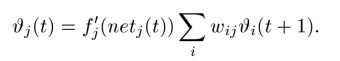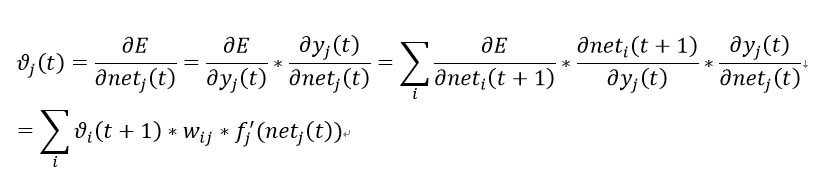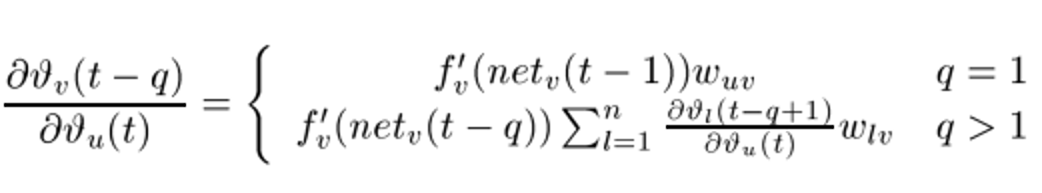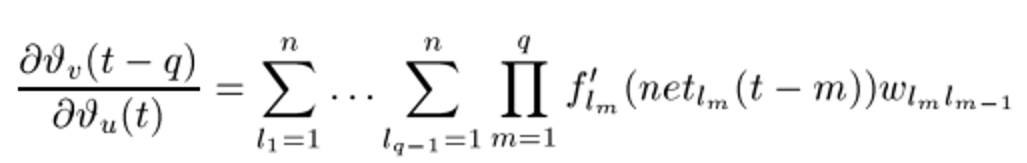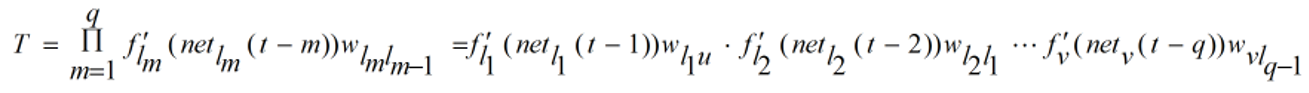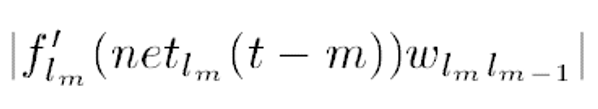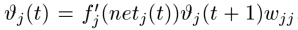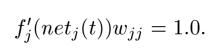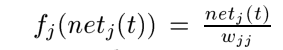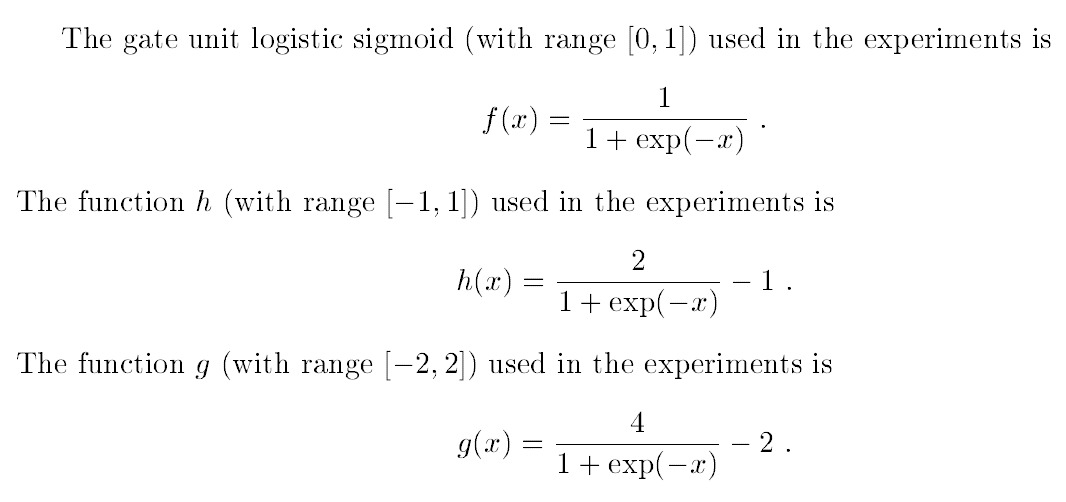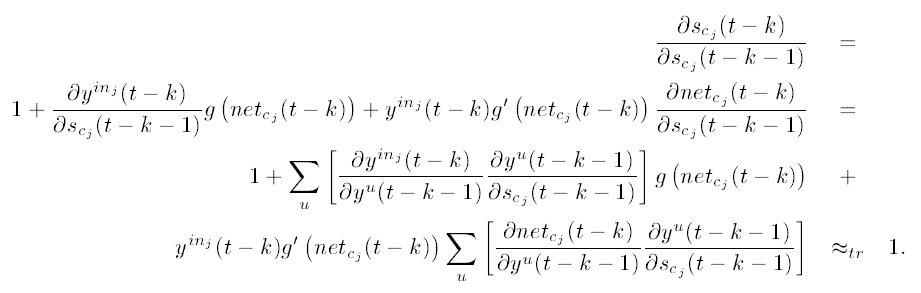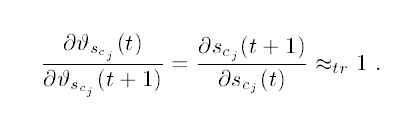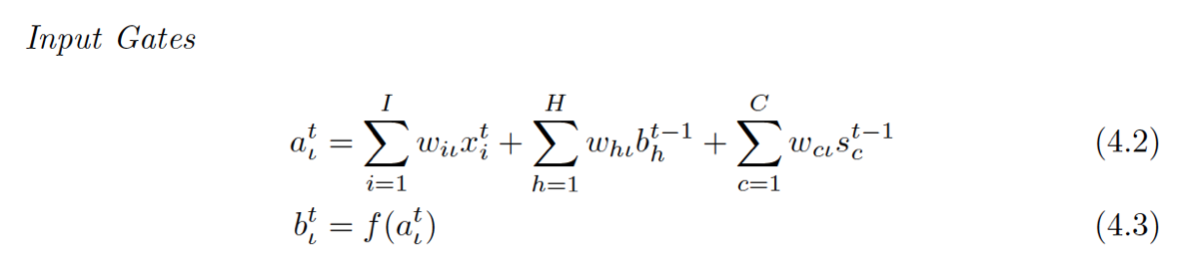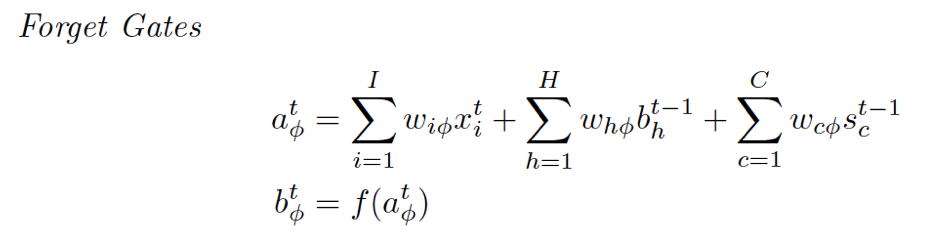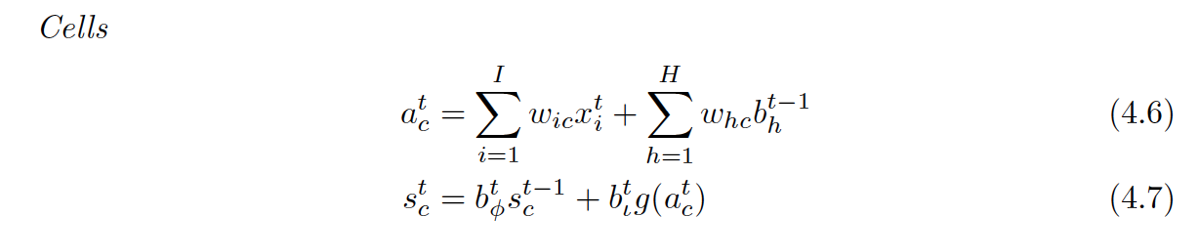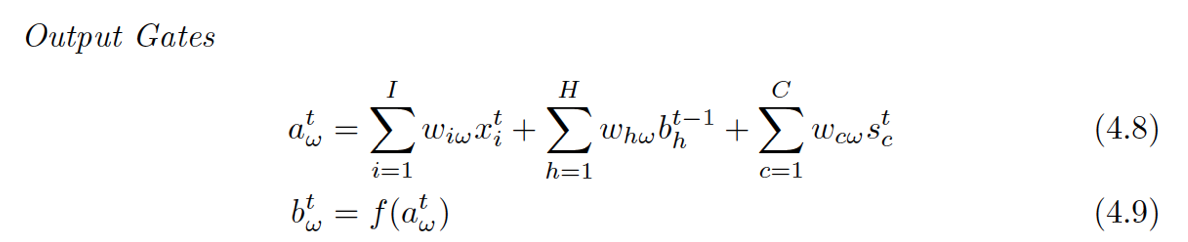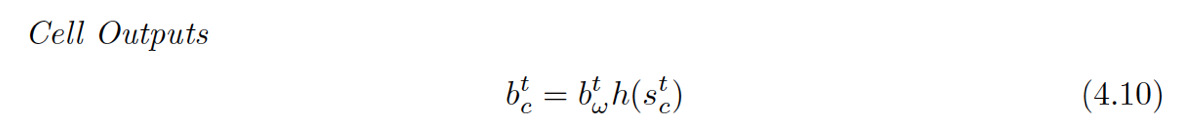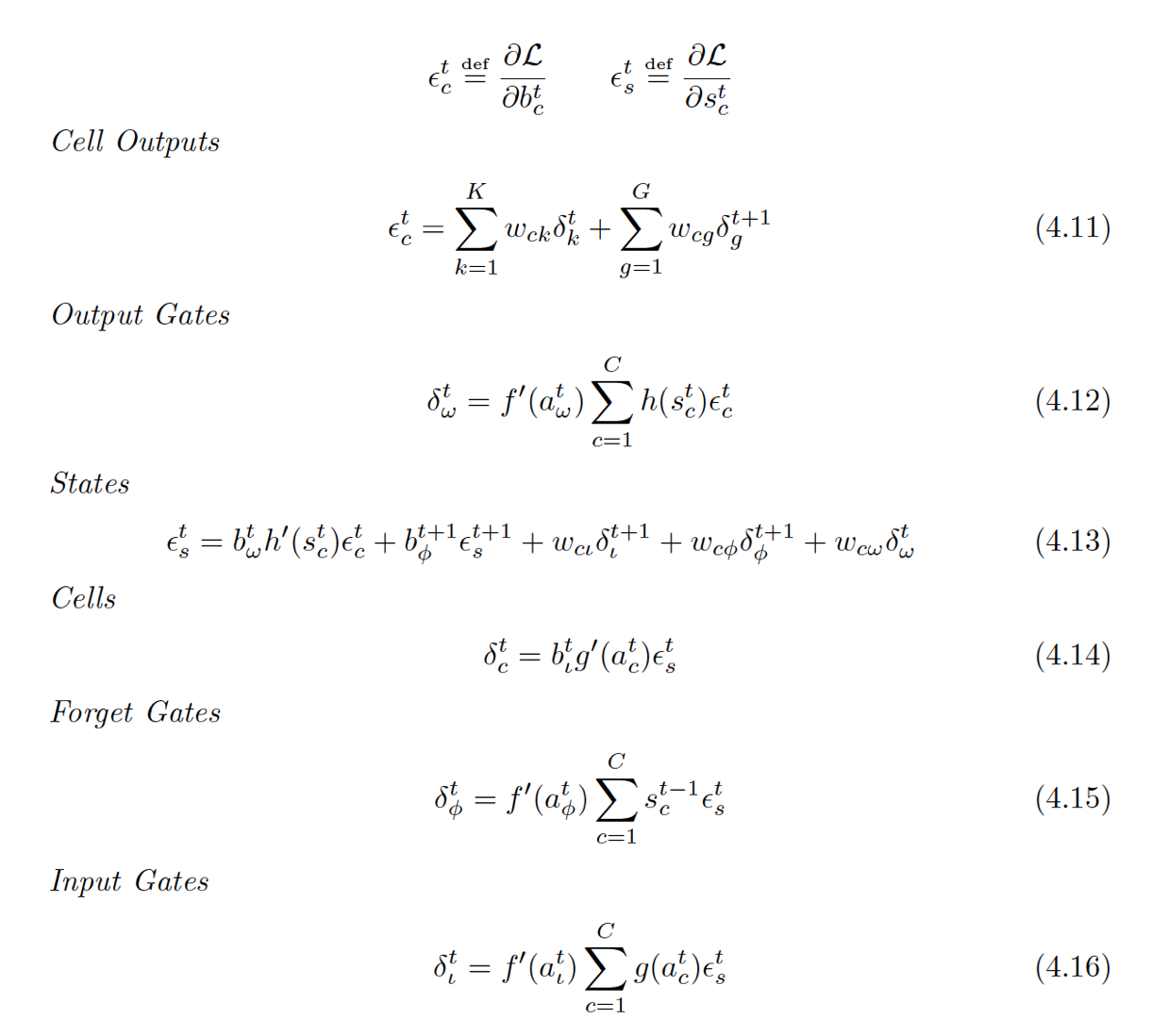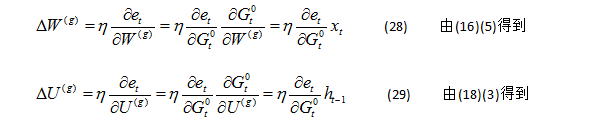系统学习深度学习（六） --LSTM总结_lstm隐层神经元的基础结构

转自：http://blog.csdn.net/shincling/article/details/49362161

https://blog.csdn.net/app_12062011/article/details/54424986

1. 概念：

Long short-termmemory (LSTM)is a recurrent neuralnetwork (RNN)architecture (an artificialneural network)published^[1] in 1997 by Sepp Hochreiter and Jürgen Schmidhuber. Like most RNNs, an LSTM network is universalin the sense that given enough network units it can compute anything aconventional computer can compute, provided it has the proper weight matrix, which may be viewed as its program. Unliketraditional RNNs, an LSTM network is well-suited to learn from experience to classify, process and predict time series when there are very long time lags of unknownsize between important events. This is one of the main reasons why LSTMoutperforms alternative RNNs and Hidden Markov Models and other sequence learning methods in numerousapplications. 

2.类属

 

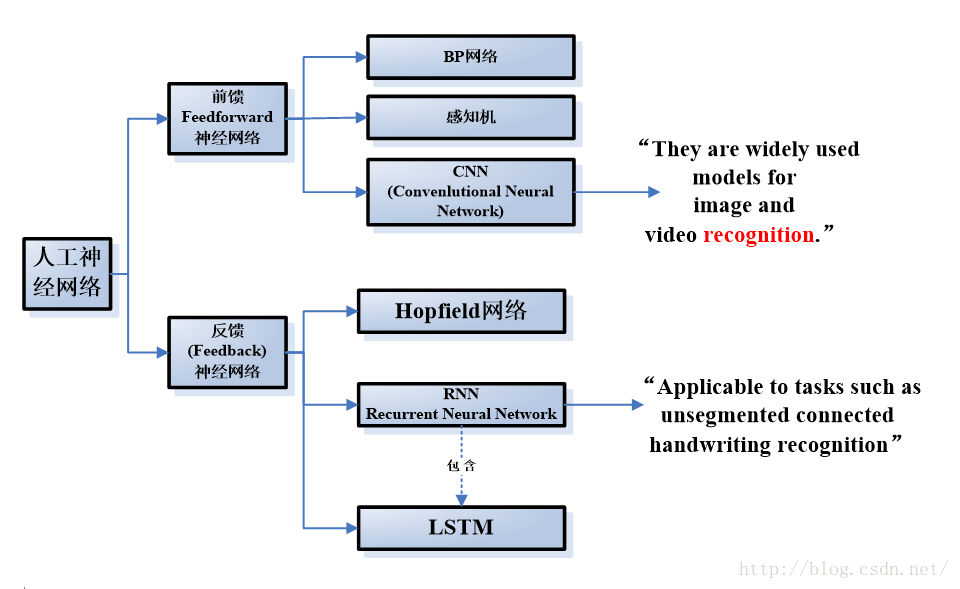
LSTM是RNN的一种变种，属于反馈神经网络的范畴。

3.模型的特点与适用性

3.1 前馈神经网络VS 反馈神经网络

在深度学习领域，传统的前馈神经网络（feed-forward neural net，简称FNN）具有出色的表现，取得了许多成功，它曾在许多不同的任务上——包括手写数字识别和目标分类上创造了记录。甚至到了今天，FNN在解决分类任务上始终都比其他方法要略胜一筹。

尽管如此，大多数专家还是会达成共识：FNN可以实现的功能仍然相当有限。究其原因，人类的大脑有着惊人的计算功能，而“分类”任务仅仅是其中很小的一个组成部分。我们不仅能够识别个体案例，更能分析输入信息之间的整体逻辑序列。这些信息序列富含有大量的内容，信息彼此间有着复杂的时间关联性，并且信息长度各种各样。例如视觉、开车、演讲还有理解能力，这些都需要我们同时处理高维度的多种输入信息，因为它们时时都在变化，而这是FNN在建模时就极为匮乏的。

 3.2 CNN vs RNN

《Convolutional Networks for Images, Speech,and Time Series》，by YannLeCun & Yoshua Bengio

http://nuyoo.utm.mx/~jjf/rna/A12%20Convolutional%20networks%20for%20images,%20speech,%20and%20time%20series.pdf
尤其是这一段：
While characters or short spoken words can besize-normalized and fed to a fixed-size network, more complex objects such aswritten or spoken words and sentences have inherently variable size. One way ofhandling such a composite object is to segment it heuristically into simplerobjects that can be recognized individually, e.g. characters phonemes. However,reliable segmentation heuristics do not exist for speech or cursivehandwriting. A bruteforce solution.....
简单的说，CNN并不完全适用于学习时间序列，因此会需要各种辅助性处理，且效果也不一定好。面对对时间序列敏感的问题赫和任务，RNN(如LSTM)通常会比较合适。

一个例子：

Task 1 - Sentiment analysis: You're given some review, and youwant to predict the rating of the review. 
Task 2 - Machine translation: Translate a sentence from some source language totarget language.
Now, the basic difference in terms of applicability of conv-net and RNN is thatconv-nets (like most other machine learning algorithm) take a fixed size inputand generate fixed-size outputs. RNN, on the other hand, can handle arbitraryinput/output lengths, but would typically require much more data compared toconv-nets because it is a more complex model.
Using this insight, we see that task 2 cannot be performed by conv-nets, sinceinputs and outputs are not fixed-length. So RNNs for task 2.
For task 1, however, you can use RNN if you have a lot of data. But you canalso use conv-nets - fix the length of the input, and adjust the input lengthby truncating or padding the actual input. Note that this will not affect thesentiment of the review much, so this is a reasonable approach. And since it'sa 1D convolution, that is typically used in sequences, it is called temporalconvolution. Conceptually, it is similar to 2D spatial convolution.

小结：

RNN回归型网络，用于序列数据，并且有了一定的记忆效应，辅之以lstm。
CNN应该侧重空间映射，图像数据尤为贴合此场景。

3.3 LSTM vs (传统)RNNs

两篇文章的描述：

1.     AlexGraves. 《SupervisedSequence Labelling with Recurrent Neural Networks》. Textbook, Studies inComputational Intelligence, Springer, 2012.

“Long Short-term Memory (LSTM) is an RNN architecture designed to be better at storing and accessing information thanstandard RNNs. LSTM has recently given state-of-the-art results in a variety ofsequenceprocessing tasks, including speech andhandwriting recognition .”

2.    Yann LeCun、Yoshua Bengio和Geoffrey Hinton合作的这篇综述文章《Deep Learning》

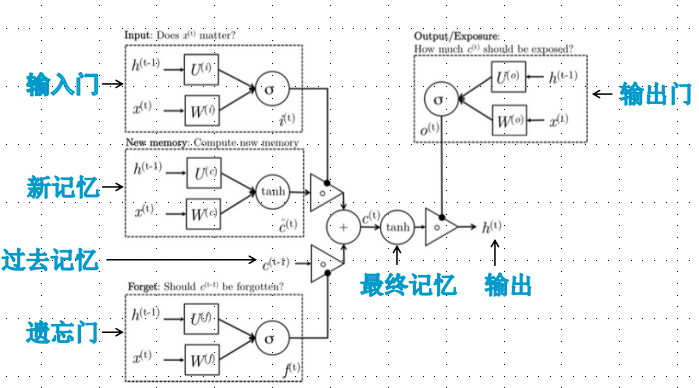
“RNNs一旦展开（如图5），可以将之视为一个所有层共享同样权值的深度前馈神经网络。虽然它们的目的是学习长期的依赖性，但理论的和经验的证据表明很难学习并长期保存信息。

为了解决这个问题，一个增大网络存储的想法随之产生。采用了特殊隐式单元的LSTM（long short-termmemory networks）被首先提出，其自然行为便是长期的保存输入。一种称作记忆细胞的特殊单元类似累加器和门控神经元：它在下一个时间步长将拥有一个权值并联接到自身，拷贝自身状态的真实值和累积的外部信号，但这种自联接是由另一个单元学习并决定何时清除记忆内容的乘法门控制的。

LSTM网络随后被证明比传统的RNNs更加有效，尤其当每一个时间步长内有若干层时，整个语音识别系统能够完全一致的将声学转录为字符序列。目前LSTM网络或者相关的门控单元同样用于编码和解码网络，并且在机器翻译中表现良好。”

4.在不同任务上的数据对比

数据尽管在检索上还有一些问题，尤其是 WOS数据库上涵盖的文章可能代表了一部分水平比较高的论文，在数量上并不完全按与研究的力度划等号，但还是可以看出一些端倪。

CNN大部分的任务都是跟分类相关的，在处理一些较为复杂的任务上的应用暂时还比较匮乏。而LSTM在近年来尤其发展迅猛，在处理序列相关的任务时的应用较为广泛。

5.结论

LSTM是RNN的一个优秀的变种模型，继承了大部分RNN模型的特性，同时解决了梯度反传过程由于逐步缩减而产生的Vanishing Gradient问题。具体到语言处理任务中，LSTM非常适合用于处理与时间序列高度相关的问题，例如机器翻译、对话生成、编码\解码等。

虽然在分类问题上，至今看来以CNN为代表的前馈网络依然有着性能的优势，但是LSTM在长远的更为复杂的任务上的潜力是CNN无法媲美的。它更真实地表征或模拟了人类行为、逻辑发展和神经组织的认知过程。尤其从2014年以来，LSTM已经成为RNN甚至深度学习框架中非常热点的研究模型，得到大量的关注和研究。

LSTM理论推导总结

目录

1.     传统RNN的问题：梯度的消失和爆发

2.     LSTM对问题的解决方式

3.     LSTM对模型的设计

4.     LSTM训练的核心思路和推导

5.     近期LSTM的模型的改进

6.     LSTM的工作特性的研究

7.     一些可能存在的问题

8.     总结

9.     参考文献

 

1.传统RNN模型的问题：梯度的消失和爆发

接下来的推导主要源自LSTM的作者的论文《THE VANISHING GRADIENT PROBLEM DURING recurrent neural networks and problem solutions》

以及作者在提出LSTM的论文的前半部分也有一样的内容。

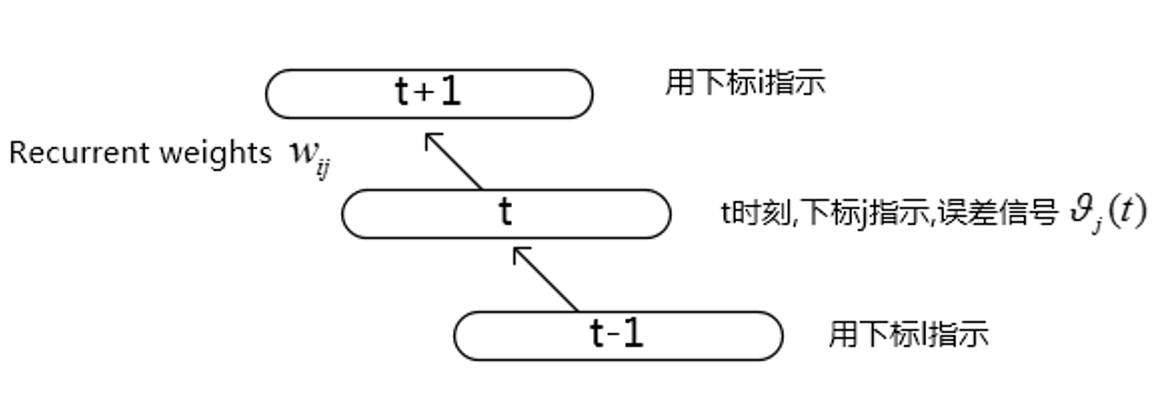
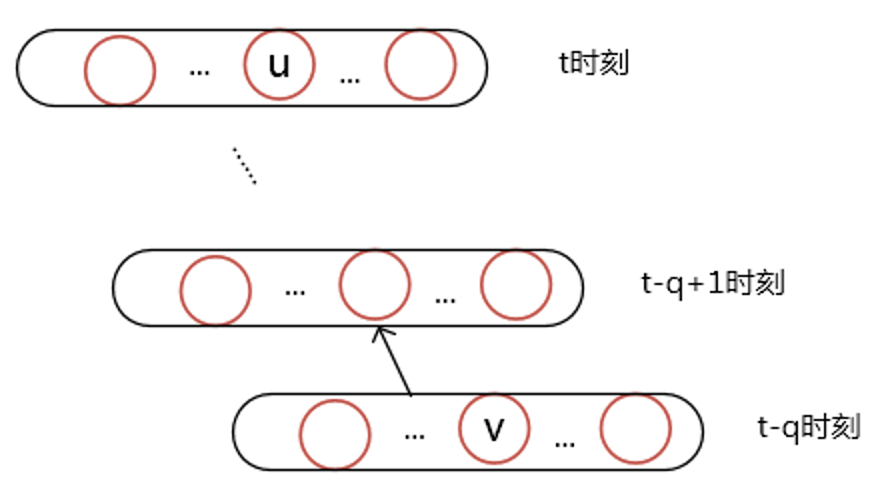
先看一下比较典型的BPTT（Back propgation through time)一个展开的结构，如下图，这里只考虑了部分图。

对于t时刻的误差信号计算如下：

推导公式如下：

上面的公式在整个BPTT乃至整个BP网络里都是非常常见的了。具体推导如下，做个演示：

那么如果这个误差信号一直往过去传呢，假设任意两个节点u, v他们的关系是下面这样的：

那么误差传递信号的关系可以写成如下的递归式：

n表示图中一层神经元的个数，这个公式不难理解，要求从t时刻某节点u传递到t-q时刻某节点v的误差，那么就需要先求出u传递到t-q+1时刻所有节点的误差之后，再进行相邻两层之前的回传（也就是之前那个公式）。

这显然是一个递归的过程，把里面连乘展开看：

看起来比较复杂，事实上可以这么说：

前面的q-1个加和符号，就是在误差回传过程中，从u到v遍历了所有中间层的可能的链接起来的路径。

后面的连乘法就是其中一条路径的误差表示，总共经历了q个层，每一层都要经过一个激活函数的导数和权值相乘。

展开来看，把后面的这个连乘的式子叫做T的话：

整个结果是对T求和的次数是n^(q-1), 即T有n^(q-1)项

而每一个T经过了q次这样的系数的乘法：

如果上式> 1, 误差就会随着q的增大而呈指数增长，那么网络的参数更新会引起非常大的震荡。

如果上式< 1， 误差就会消失，导致学习无效，一般激活函数用sigmoid函数，它的倒数最大值是0.25, 权值最大值要小于4才能保证不会小于1。

误差呈指数增长的现象比较少，误差消失在BPTT中很常见。

到这里，我们大致应该可以明白了，由于经过每一层误差反传，就会引入一个激活函数的导数的乘子，所以导致经过多步之后，这个乘子的连乘会导致一系列麻烦，即我们所谓的梯度消失和爆发的问题。

事实上，上面这个式子结果的分析是非常复杂的，因为我们可以调节w和增加每一层的节点数n来对结果进行调节。但是事实上这些做法都不能完善的解决，因为w是每一层都共享的参数，它会影响net的值，而net值的变化会对激活函数的导数有影响。

举个例子，即便把w变成无限大，那么导致net也会无限大，导致激活函数的导数为0。

事实上原文也对这些问题进行了分析，并且验证了上面说道的两个问题，但是更深入的分析是一个非常复杂的情况，涉及到高阶无穷小和w的调节等一系列动态的问题。作者在原文中都没有继续说清楚。

更加深入的理解这个问题可以参照这篇论文，

《On the difficulty of training Recurrent Neural Networks》Razvan Pascanu，Tomas Mikolov，Yoshua Bengio

这里面深入讨论了vanishing and the exploding gradient 的本质（w矩阵特征值等复杂的原理），和他们带来的一些现象。

梯度消失和爆发不是这篇文章的重点，所以我暂时写到这里，总结一下，对于常见的梯度消失问题来说：

      传统的RNN模型，在训练的过程中的梯度下降过程中，更加倾向于按照序列结尾处的权值的正确方向进行更新。也就是说，越远的序列输入的对权值的正确变化所能起到的“影响”越小，所以训练的结果就是往往出现偏向于新的信息，即不太能有较长的记忆功能。

2.LSTM对问题的解决方式

注意，下面这部分是原版LSTM的解释，而真正最近很火的LSTM，是对原版的改进。

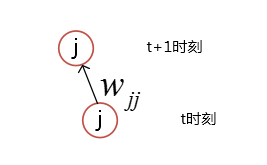
为了克服误差消失的问题，需要做一些限制，先假设仅仅只有一个神经元与自己连接，简图如下：

根据上面的，t时刻的误差信号计算如下：

为了使误差不产生变化，可以强制令下式为1：

根据这个式子，可以得到：

这表示激活函数是线性的，常常的令fj(x) = x, wjj = 1.0，这样就获得常数误差流了，也叫做CEC（constant error carrousel）。

3.LSTM对模型的设计

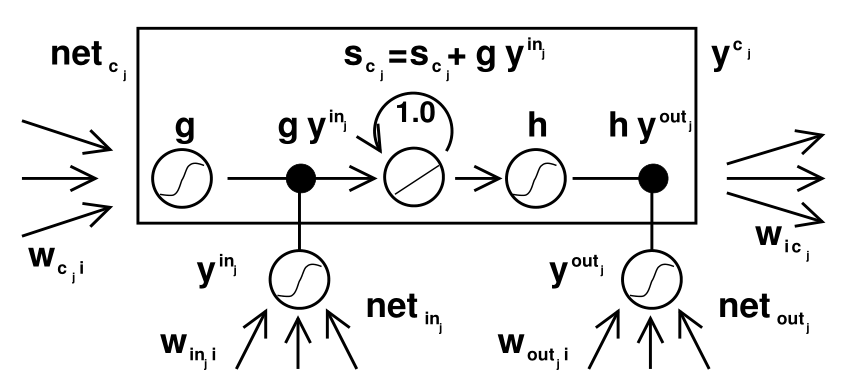
到上面为止，提出的最简单的结构其实可以大致用这样一个图表述：

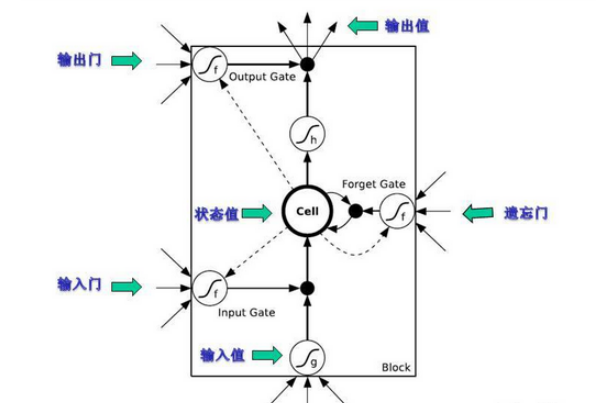
但是光是这样是不行的，因为存在输入输出处权值更新（原文作者的原话，本段末尾后面进行一些解释）的冲突，所以加上了两道控制门，分别是input gate, output gate，来解决这个矛盾，图如下：

 

图中增加了两个控制门，所谓控制的意思就是计算cec的输入之前，乘以input gate的输出，计算cec的输出时，将其结果乘以output gate的输出，整个方框叫做block, 中间的小

圆圈是CEC, 里面是一条y = x的直线表示该神经元的激活函数是线性的，自连接的权重为1.0

输入输出权值矛盾，作者的原文中这样描述的：

说实话，仅就这一段，我读了不下几十次，跟几个师兄也探讨过很多次，依然没有找到一个很好的解释来达成共识。

从我个人角度的理解这个加了Gate的动机，我简单这样阐述一下：

（1）加入了门，其实是一种多层次的特征的选择方式。

举个不恰当的例子，例如我去面试百度，首先我可能需要经过一个技术面，看看我是否具备相应的技术素质来进入公司。

通过之后，我又经历了一个人力面，看看我其他的素质是否满足。当然，原则上我们只需要一次面试同时测试我的技术和人力素质都可以了。

但是，这就对面试官提出了更高的要求，这个面试官又得懂技术，又得很懂人力。显然这样综合的素质我们很难满足，而用两个层次不同的面试，我们比较容易做到。

这个技术面我们可以类比成图上的 netcj ，人力面我们可以类比成为input gate。

我们当然可以在进入cell核心单元之前，用一套w得到我们想要的信息。

但是这个难度就非常地大，想要训练出来这个W就比用两个层次的来筛选难得多。

（2）各个Gate功能有些重复，作者也提到了输入输出Gate有时候不需要同时出现，可以只用其中一个。

4.LSTM训练的核心思路和推导

到此为止，我们大致有了这样的印象，作者还是比较“任性”地创造了这么一个模型，在理论上坚定了一个叫CEC的恒定误差流，在这个核心思想上又加入了一些Gate，在这里带来了另外一个问题，加入了Gate之后的结构，已经与之前的核心简单结构不符，在训练过程中，必然地在一个Block里面，误差会发生传播，弥散作用于不同的Gate，导致梯度被分散，可能依然会带来梯度消失的问题。如何解决？

作者给出的解决方法是：设计与结构相适应的训练算法，来保持CEC功能的完整。这里用到的想法是截断梯度回传（truncated backprop version of the LSTM algorithm）。

这个算法的思想是：为了保证在Memory cell的内部的误差不会衰减，所有到达这个Block的输入误差，包括(net_cj , net_inj, net_outj ) , 不会继续朝更前一个时间状态进行反向传播。

形象化地描述这个过程：当一个误差信号到达一个Block的output时（通过隐层和输出层的回传），首先被输出门的激活函数和导数 h’进行尺度变换（scaled）， 之后成为了CEC状态的值往之前的时刻进行传递，当这个误差要通过Input gate和g离开这个某个时刻的Block的时候，它再次经过激活函数和g’的变换，然后此刻的误差在进入到前一个时间状态的Block之前（详细的看下文，这里没说清楚全部），对与它链接的一些权重进行更新。具体的实现过程，来进行一下推导。

在这里有个小细节需要注意下，原文中使用的h和g都不是现在广为使用的tanh和sigmoid，而是sigmoid的一些变种，如：

个人经验：

对于有递归的结构的某些单元，使用有正负差异的激活函数效果更好一点。

之后对LSTM的截断回传算法进行一个细致的推导，参见原文的附录。

PS: 这部分的推导，我在两次报告中，都是按照LSTM原文中附录的推导进行完整的讲解，这中间的公式非常多（40个），所以在这里不推了。主要的几个重要的公式在这里列出来：

（1）截断梯度法的近似

简单解释一下，误差回传到 input / output gate 和一个Cell的输入（netcj)之后，不会向上一个时刻回传误差，而只用来在这里更新各个部分的权值w。

根据上式的推导，可以得到的另外几个关键公式如下：

在Memory cell中的各个t时刻的误差，保持一致。

最后整个梳理一下误差回传的过程，误差通过输出层，分类器，隐层等进入某个时刻的Block之后，先将误差传递给了Output Gate和Memory Cell两个地方。

到达输出门的误差，用来更新了输出门的参数w，到达Memory Cell之后，误差经过两个路径，

1是通过这个cell向前一个时刻传递或者更前的时刻传递，

2是用来传递到input gate和block的输入，用来更新了相应的权值（注意！不会经过这里向前一个时刻传递误差）。

最关键最关键的问题再重复一遍就是，这个回传的算法，只通过中间的Memory Cell向更前的时刻传递误差。

5.近期LSTM的模型的改进

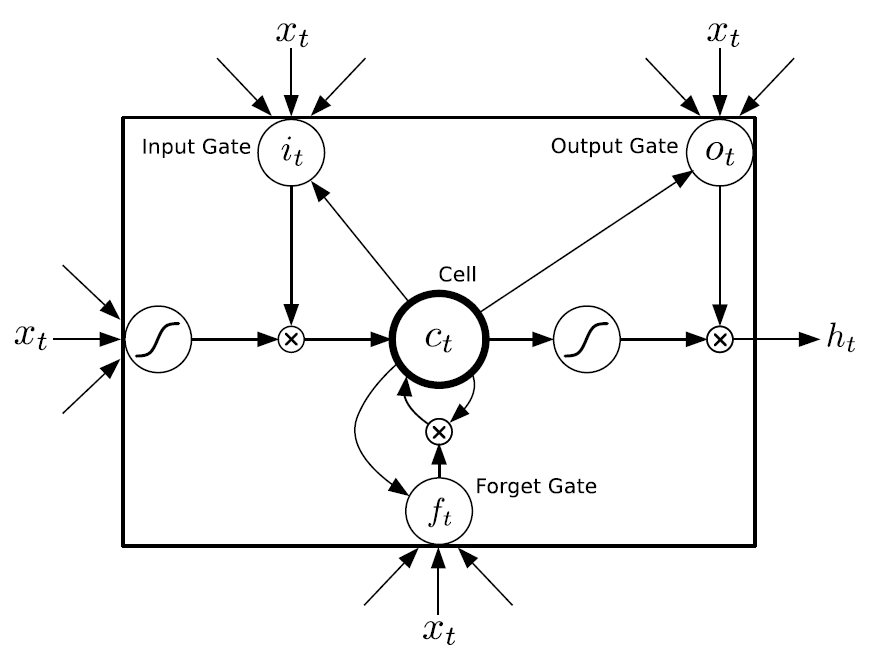
（注意这里角标顺序回归正常，从前到后）

与97年LSTM的原型想必，主要改动的几点：

1.     引入了Forget门，有些文献也叫做Keep Gate（其实这个叫法我觉得更好）。

2.      激活函数的选择有所改变，通常就是sigmoid和tanh。

3.     加入了Peephole，即Celll对各个Gate的链接。

4.     训练过程不再使用截断算法，而是用FULL BPTT+一些trick进行算法，且获得的更好效果。

(The original LSTM algorithm used a custom designed approximategradient calculation that allowed the weights to be updated after everytimestep .However the full gradient can instead be calculated with backpropagation through time , the method used in this paper. One difficultywhen training LSTM

with the full gradient is that the derivatives sometimes become excessively large, leading to numerical problems. To prevent this, allthe experiments in this paper clipped the derivative of the loss with respectto the network inputs to the LSTM layers (before the sigmoid and tanh functionsare applied) to lie within a predefined range)

新的一些模型主要可以参考的文献有：

A.    Alex Graves. Supervised Sequence Labelling with Recurrent Neural Networks. Textbook, Studies inComputational Intelligence, Springer, 2012.

B.    Alex Graves ,Generating Sequences With RNN

 （PS: Alex Graves 是 Hinton的学生，他前些年主要的工作就是对RNN和LSTM进行研究和应用，可以说是LSTM方面的最顶级的专家。）

具体的前向和后向推导如下：

• wij表示从神经元i到j的连接权重(注意这和很多论文的表示是反着的)
• 神经元的输入用a表示，输出用b表示
• 下标 ι, φ 和 ω分别表示input gate, forget gate，output gate 
• c下标表示cell，从cell到 input, forget和output gate的peephole权重分别记做  wcι , wcφ and wcω
• Sc表示cell c的状态
• 控制门的激活函数用f表示，g，h分别表示cell的输入输出激活函数
• I表示输入层的神经元的个数，K是输出层的神经元个数，H是隐层cell的个数

前向的计算：

误差反传更新：

（以上的公式取自Alex的论文，我懒得从原文里截图了，借用下之前提到的博客里的图。）

这块的公式的推导，比原文里要简单的多，说白了就是链式法则的反复应用，我觉得想在原理上更深入的话这个反传的推导不妨试试。其实一点都不难。

具体可以参考之前提到的博客里的内容。

补充：

这里博主省略了一些，引用另外一篇博主的补充下，主要是当下主流LSTM的推到实现。

原生的RNN会遇到一个很大的问题，叫做 The vanishing gradient problem for RNNs，也就是后面时间的节点对于前面时间的节点感知力下降，也就是忘事儿，这也是NN在很长一段时间内不得志的原因，网络一深就没法训练了，深度学习那一套东西暂且不表，RNN解决这个问题用到的就叫LSTM，简单来说就是你不是忘事儿吗？我给你拿个小本子把事记上，好记性不如烂笔头嘛，所以LSTM引入一个核心元素就是Cell。

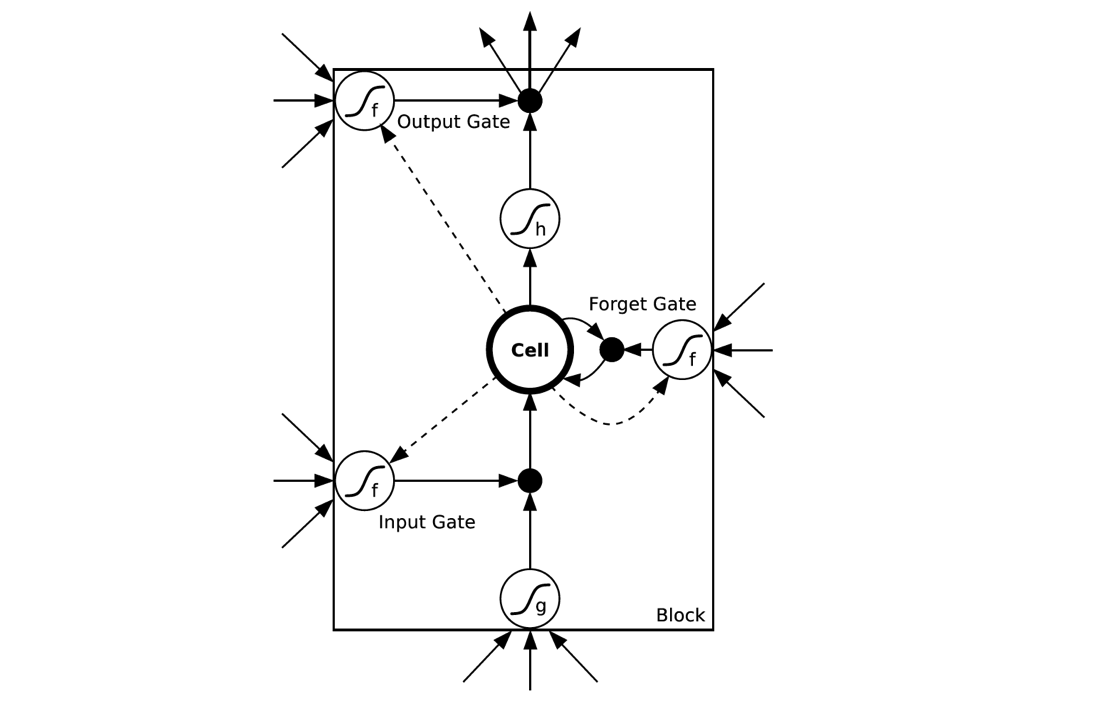
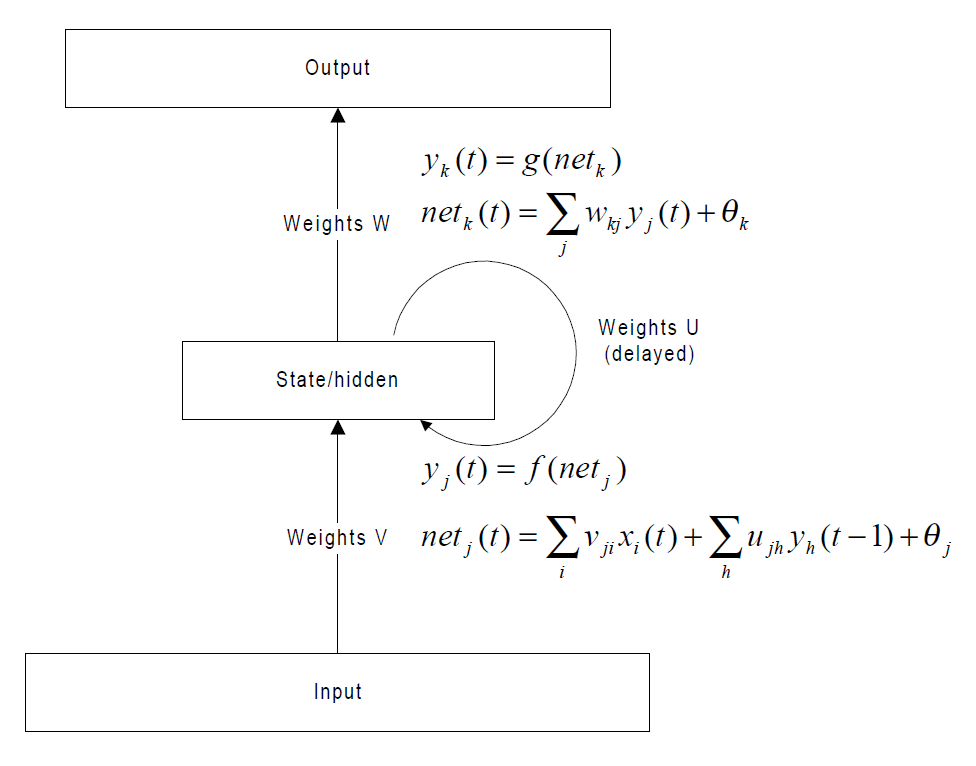
与其说LSTM是一种RNN结构，倒不如说LSTM是RNN的一个魔改组件，把上面看到的网络中的小圆圈换成LSTM的block，就是所谓的LSTM了。那它的block长什么样子呢？

怎么这么复杂……不要怕，下文慢慢帮你缕清楚。理解LSTM最方便的就是结合上面这个图，先简单介绍下里面有几个东西：

1. Cell，就是我们的小本子，有个叫做state的参数东西来记事儿的
2. Input Gate，Output Gate，在参数输入输出的时候起点作用，算一算东西
3. Forget Gate：不是要记东西吗，咋还要Forget呢。这个没找到为啥就要加入这样一个东西，因为原始的LSTM在这个位置就是一个值1，是连接到下一时间的那个参数，估计是以前的事情记太牢了，最近的就不住就不好了，所以要选择性遗忘一些东西。

在阅读下面公式说明的时候时刻记得这个block上面有一个输出节点，下面有一个输入节点，block只是中间的隐层小圆圈~~~

前向传播

一大波公式正在路上。。。。。公式均来自Alex的论文
我们按照一般算法的计算顺序来给出每个部分的公式：

Input Gate

带下标L的就是跟Input Gate相关的，回去看上面那个图，看都有谁连向了Input Gate：外面的输入，来自Cell的那个虚线（虚线叫做peephole连接），这在公式立体现在4.2的第一项和第三项，计算就是普通的累积求和。那中间那个是个什么鬼？
带H的是一个泛指，因为LSTM的一个重要特点是其灵活性，cell之间可以互联，hidden units之间可以互联，至于连不连都看你（所以你可能在不同地方看到的LSTM公式结构都不一样）所以这个H就是泛指这些连进来的东西，可以看成是从外面连进了的三条边的一部分。
至于4.3就是简单的激活函数计算而已

Forget Gate

再回去看那个图，连到Forget Gate都有哪些：输入层的输入、泛指的输入、来自cell的虚线，这个和Input Gate就是一回事嘛

Cells

还是老样子，回去看都有啥连到了Cell（这里的cell不是指中间那个Cell，而是最下面那个小圆圈，中间的Cell表示的其实是那个状态值S[c][t]）：输入层的输入，泛指的输入。（这体现在4.6式中）
再看看中间的那个Cell状态值都有谁连过去了：这次好像不大一样，连过去的都是经过一个小黑点汇合的，从公式也能体现出来，分别是：ForgetGate*上一时间的状态 + InputGate*Cell激活后的值

Output Gate

老样子，看谁连到了Output Gate：跟其他几个Gate好像完全一样嘛~咦，4.8那个S[c][t]为啥是t，以前都是t-1啊。
这里我也没找到相关的原因，可以理解为在计算OG的时候，S[c][t]已经被计算出来了，所以就不用使用上一时间的状态值了（同样动机不明~~这就是设定好嘛。。。）

最后最后的输出

小黑点，用到了激活后的状态值和Output Gate的结果。
一定按照图的连接来捋一捋，公式还是非常清晰的。

后向传播

又一波公式来袭。。。。。。

这次就只贴公式了，因为要每个都讲一下实在是太费功夫了，记住一个要点就是『看上面的图！！』，看看每个要求偏导的东西都有谁会反向传回东西给它，可以看到最复杂的就是4.13了，因为这是对那个状态值求导，它不光连向了三个门（公式后三项，两个本下一时刻，FG是本时刻的），还连向了最后的输出b[c][t]（公式第一项）以及下一时刻的自己（公式第二项），反向传播公式推导用到的唯一数学工具就是链式法则，你要觉得求偏导看不懂，就把它拆成链看就好了。

还有一点，记得最后的Loss Function是每一时间的一个求和，所以当你算当前层输出层传回来的残差都时候就可以忽略其它东西了，举个例子：4.11是对b[c][t]求偏导，而b[c][t]是正向传播LSTM block的输出，输出到谁了？当前层的输出层，下一层的Hidden Layer，这两个东西的最后的Loss function是分开的，彼此之间没有关系，所以公式里是两部分相加。4.11中的G和之前的H一样，也是泛指，因为它不一定只输出到下一时间的自己，可能还会到下一时间的其他隐层unit，G代表什么纯看你怎么确定的网络结构。

6.LSTM的工作特性的研究

事实上，到目前为止，大部分的LSTM的模型和语言模型、手写体识别、序列生成、机器翻译、语音、视频分析等多种任务中取得了一些成功的应用，但是很少有人去研究到底是什么原因导致了这些情况的发生，以及哪些设计是切实有效的。

《Visualizing and Understanding Recurrent Networks》 Andrej Karpathy，Justin Johnson，Li Fei-Fei

这篇文章是斯坦福的李菲菲老师指导的她的学生的一片文章，提供了一些思路。（这个文章的各类图表真的非常炫目，毕竟李菲菲老师团队的前端的功力了得）。

对各个门之间的状态，在字母级别的语言序列和语言模型中做了一系列实验，并且对RNN和GRU模型也做了对比实验。

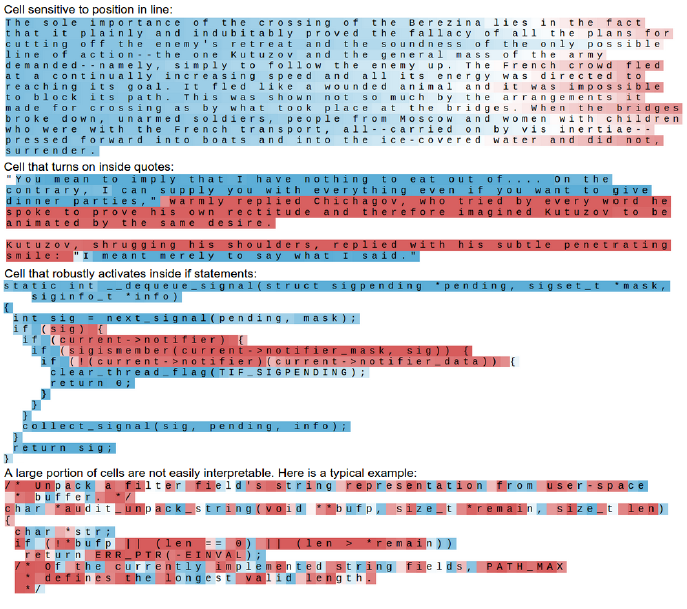
这里简单说一下比较有趣的一点，如下，这篇文章的实验是用了《战争与和平》和Linux的源码（！！！）两个数据集上做的。

作者非常惊喜地发现，LSTM的记忆单元中的某些Units有着令人惊喜的功能，比如它们可能会标志着段落的结束、或者引用内容，或者linux的源码中的一些条件语句的内容。

当然，大部分都是我们难以解释的一些隐层状态。

另外这篇文章也提到如，

K. Greff, R. K. Srivastava, J. Koutn´ık, B. R. Steunebrink, and J.Schmidhuber. LSTM: A search space

odyssey. CoRR, abs/1503.04069, 2015.

这篇文章也做了一些实验，并提出了这样的结论：

“The forget gates are its most criticalcomponents”

遗忘门，起到了最为关键的作用。（而LSTM原型中压根就没有遗忘门......)

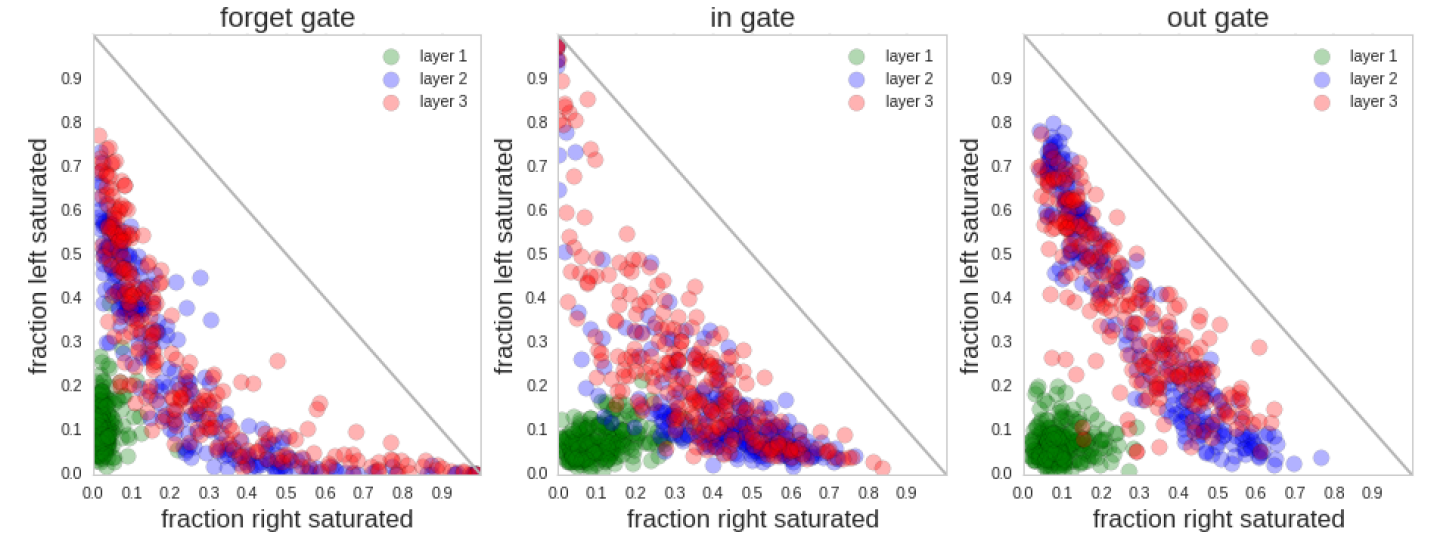
另外这篇文章也提到了各个门的状态的一些统计信息，

大致情况可以这样表述，forget门倾向于为不激活状态（偏向0），即频繁忘记东西。

Input Gate倾向于通常出于打开的状态。

Output gate则有开有闭，基本平衡。

7.一些可能存在的问题

1.     Theano LSTM 例程里的梯度回传算法，由于Theano自动求导的功能，在回传时候应该是采用的是FULL BPTT，这个是不是会带来一些如之前所说的问题？

    答：这个问题我在之前其实已经说明了Alex的一些Trick的做法。仔细思考下，确实FULL BPTT带来的梯度的问题，由于Memory Cell功能的完整性，而被缓解了。也就是说误差回传的主力还是通过了Memory Cell而保持了下来。所以我们现在用的LSTM模型，依然有比较好的效果。

2.     LSTM的Input、Output、Forget门之间的功能是不是其实有重复？有没有更简单的结构可以改进。

答：没错，例如已经出现的GRU (Gated Recurrent Unit)

8. 总结

两个关键问题：

1.      为什么具有记忆功能？

这个是在RNN就解决的问题，就是因为有递归效应，上一时刻隐层的状态参与到了这个时刻的计算过程中，直白一点呢的表述也就是选择和决策参考了上一次的状态。

2.      为什么LSTM记的时间长？

因为特意设计的结构中具有CEC的特点，误差向上一个上一个状态传递时几乎没有衰减，所以权值调整的时候，对于很长时间之前的状态带来的影响和结尾状态带来的影响可以同时发挥作用，最后训练出来的模型就具有较长时间范围内的记忆功能。

9.参考文献

1.     Visualizing and UnderstandingRecurrent Networks

2.     on the difficulty of trainingrecurrent network

3.     Hochreiter97_lstm

4.     Oxford , Rnn & LSTM

5.     THE VANISHING GRADIENT PROBLEMDURING RNN

6.     RECURRENT NEURAL NETWORKREGULARIZATION

7.     A. Graves. Supervised SequenceLabelling with Recurrent Neural Networks.

8.     A guide to recurrent neuralnetworks and back-propagation

9.     An Empirical Exploration ofRecurrent Network Architectures

10.  A survey on the application ofrecurrent neural networks to statistical language modeling

11.  Generating Sequences With RNN _Alex graves

12.  On the Properties of NeuralMachine Translation Encoder–Decoder 1409 1259v2

13.  Encodere mechaine translationuse CNN 1503.01838v5

补充一个源码Demo

LSTM隐层神经元结构：

LSTM隐层神经元详细结构：