机器学习模型/算法—— 阶段性总结（1）模型框架：假设函数、目标函数和优化算法_假设函数和目标函数的区别

机器学习算法/模型分类：

• 监督学习
  分类、回归
• 无监督学习
  聚类、降维
• 强化学习

0. 相关概念（记录）

• 损失函数、经验风险、结构风险
  目标函数 = 结构风险函数 = 经验风险函数 + 正则项
• Hessian矩阵正定
  一阶导数信息：梯度
  二阶导数信息：Hessian矩阵
  正定（positive definite）的直观理解：正定矩阵A使得向量经过 Ax 变换后与变换之前的夹角恒定小于 $\frac{\pi }{2}$。

…

1. 从假设函数到目标函数

对于几乎所有机器学习算法，无论是有监督学习、无监督学习，还是强化学习， 最后一般都归结为求一个目标函数的极值，即最优化问题。

首先，要明白下面几个点：

1. 什么是假设函数？
2. 什么是目标函数？
3. 目标函数和损失函数的关系？

• 假设函数是一个近似目标函数的候选模型，用于表示输入样本到输出样本之间的映射关系。 (参考
  )
• 目标函数是最终需要优化的函数，其中包括经验损失和结构损失，即目标函数 = 经验损失 + 结构损失（obj=loss+Ω）

说白了，在没有正则项的情况下，我们所说的损失函数也就是我们的目标函数，即目标函数 = 损失函数；当包含正则项时，目标函数 = 损失函数 + 正则项。

借用知乎上乎友的回答（看图）：

1.1 有监督模型

对于有监督学习，有两类情况：

（1）我们要找到一个最佳的映射函数f(x)，假设映射函数为：

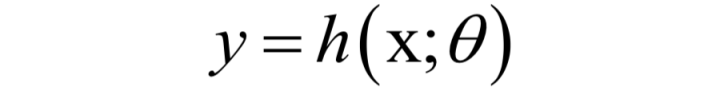
（其中θ是模型的参数，如何确定它的值，是训练算法的核心）

目标是使得对训练样本的损失函数最小化（最小化经验风险或结构风险）：

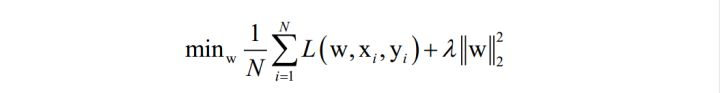
在这里，N为训练样本数，L是对单个样本的损失函数，w是要求解的模型参数，是映射函数的参数， x_i 为样本的特征向量，y_i 为样本的标签值。

（2）或者是找到一个最优的概率密度函数p(x)，

使得对训练样本的对数似然函数极大化（最大似然估计）：

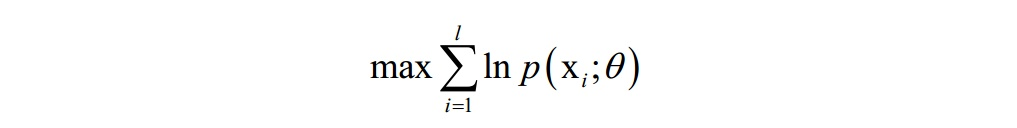
在这里，θ 是要求解的模型参数，是概率密度函数的参数。

(本来是似然函数的最大化问题，但是连乘求导不方便，因此对似然函数取对数，得到对数似然函数)

1.2 无监督学习

（1）对于无监督学习的聚类问题，机器学习算法要寻找一个集合的划分，将样本集D划分成多个不相交的子集：

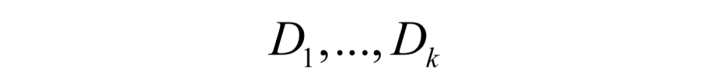
目标函数：
以聚类算法为例，算法要是的每个类的样本离类中心的距离之和最小化：

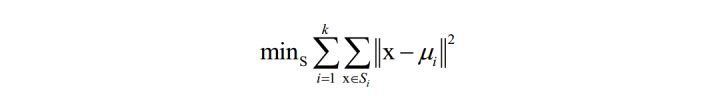
在这里k为类型数，x为样本向量， μ_i 为类中心向量， S_i 为第 i 个类的样本集合。

（2）对于数据降维问题，机器学习算法要寻找一个映射函数，将一个高维向量映射成一个低维向量：

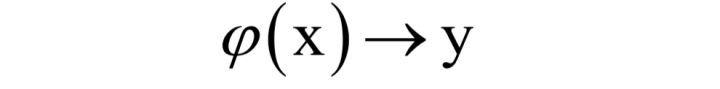
但要尽可能的保留之前向量的一些重要信息。

1.3 强化学习

对于强化学习，机器学习算法要为每种状态s下确定一个动作a来执行，即确定策略函数，使得执行这些动作之后得到我们预期的结果：

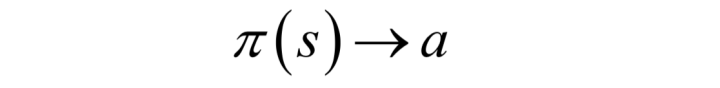
目标函数：
我们要找到一个最优的策略，即状态s到动作a的映射函数（确定性策略，对于非确定性策略，是执行每个动作的概率
使得任意给定一个状态，执行这个策略函数所确定的动作a之后，得到的累计回报最大化：

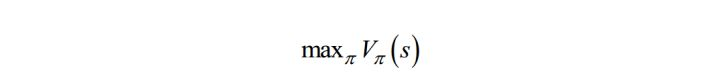
这里使用的是状态价值函数。

总体来看，机器学习的核心目标是给出一个模型（一般是映射函数），然后定义对这个模型好坏的评价函数（目标函数），求解目标函数的极大值或者极小值，以确定模型的参数，从而得到我们想要的模型。
这也是机器学习概念部分讲的机器学习三步。

附：常用的一些损失函数以及它们的导数：

需要说明的是，对前面介绍的很多损失函数，我们都可以加上正则化项，得到新的损失函数，以减轻过拟合。

2. 最优化算法

最优化算法：

公式法
|
近似法（数值优化）
|
随机搜索法

---

除了极少数问题可以用暴力搜索来得到最优解之外，我们将机器学习中使用的优化算法分成两种类型（不考虑随机优化算法如模拟退火、遗传算法）：

• 公式法：梯度为 0 的方程组直接求解
• 数值优化（近似求解）：利用一阶、二阶导数，如迭代法

前者给出一个最优化问题精确的公式解，也称为解析解，一般是理论结果。
对绝大多数函数来说，梯度等于0的方程组是没法直接解出来的，如方程里面含有指数函数、对数函数之类的超越函数。对于这种无法直接求解的方程组，我们只能采用近似的算法来求解，即数值优化算法。

除此之外，还有其他一些求解思想，如分治法，动态规划等。

一个好的优化算法需要满足：

• 能正确的找到各种情况下的极值点
• 速度快

关系总结如下：

2.1 公式法

• 费马定理
• 拉格朗日乘数法
• KKT条件
  KKT条件是拉格朗日乘数法的推广，用于求解既带有等式约束，又带有不等式约束的函数极值。

2.2 数值优化算法（近似求解）

• 梯度下降
  梯度下降法沿着梯度的反方向进行搜索，利用了函数的一阶导数信息。

梯度下降法的迭代公式为：

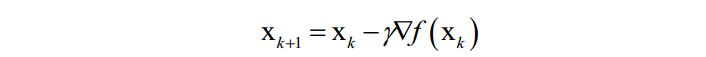
• 动量法
  为了加快梯度下降法的收敛速度，减少震荡，引入了动量项。
  动量项累积了之前迭代时的梯度值，加上此项之后的参数更新公式为：
  
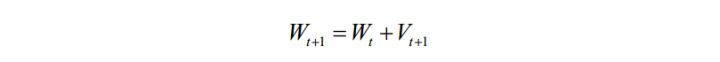
  其中 V_t+1 是动量项，它取代了之前的梯度项。动量项的计算公式为：
  
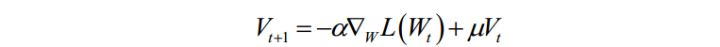
  它是上一时刻的动量项与本次梯度值的加权平均值，其中 $\alpha$ 是学习率，μ 是动量项系数。
• AdaGrad算法
  AdaGrad算法是梯度下降法最直接的改进。梯度下降法依赖于人工设定的学习率，如果设置过小，收敛太慢，而如果设置太大，可能导致算法那不收敛，为这个学习率设置一个合适的值非常困难。

AdaGrad算法根据前几轮迭代时的历史梯度值动态调整学习率，且优化变量向量x的每一个分量 x_i 都有自己的学习率。参数更新公式为：

• Adam算法

Adam算法整合了自适应学习率与动量项。算法用梯度构造了两个向量m和v，前者为动量项，后者累积了梯度的平方和，用于构造自适应学习率。它们的初始值为0，更新公式为：

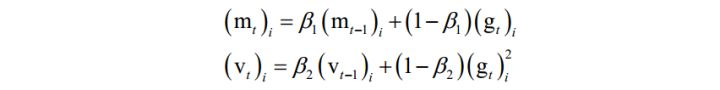
其中 β₁ ， β₂ 是人工指定的参数，i 为向量的分量下标。依靠这两个值构造参数的更新值，参数的更新公式为：

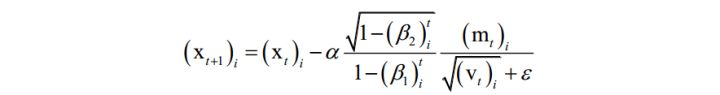
在这里，m类似于动量项，用v来构造学习率。

• 随机梯度下降法

批量随机梯度下降法在每次迭代中使用上面目标函数的随机逼近值，即只使用M [公式] N个随机选择的样本来近似计算损失函数。

• 牛顿法
  牛顿法是二阶优化技术，利用了函数的一阶和二阶导数信息，直接寻找梯度为0的点。牛顿法的迭代公式为：
  
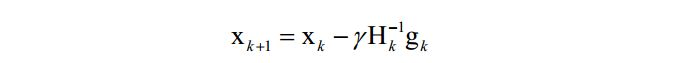
  其中H为Hessian矩阵，g为梯度向量。牛顿法不能保证每次迭代时函数值下降，也不能保证收敛到极小值点。

• 拟牛顿法

2.3 分治法

分治法是一种算法设计思想，它将一个大的问题分解成子问题进行求解。根据子问题解构造出整个问题的解。在最优化方法中，具体做法是每次迭代时只调整优化向量x的一部分分量，其他的分量固定住不动。

• 坐标下降法
• SMO算法

2.4 动态规划算法

• 隐马尔可夫模型的解码算法（维特比算法）
• 强化学习中的动态规划算法

3. 模型总结

一句话总结

多种角度看各种模型

信息论角度

决策边界可视化的思路

• 回归问题：直接画出决策边界（线）——将实际的预测值——y_pred当做 y ，直接画出回归线。
  （参考 线性回归）
• 分类问题：侧面显示——使用范围类的所有数据，当做新数据，去拟合模型，用得到的结果——y_pred 去上色。
  （参考 逻辑回归、SVM等）

参考

1. “假设”家族大起底！如何正确区分科学假设、统计假设和机器学习假设？

2. 机器学习中的最优化算法总结

3. 机器学习–>期望风险、经验风险与结构风险之间的关系

4. 浅谈「正定矩阵」和「半正定矩阵」

5. 机器学习算法地图

6. 逻辑回归（Logistic Regression）