【数据结构】——二叉树详解

一、二叉树的定义

二叉树(Binary Tree) 是由n个结点构成的有限集(n≥0)，n=0时为空树，n>0时为非空树。对于非空树$T$：

• 有且仅有一个根结点；
• 除根结点外的其余结点又可分为两个不相交的子集$T_L$和$T_R$，分别称为$T$的左子树和右子树，且$T_L$和$T_R$本身又都是二叉树。

很明显该定义属于递归定义，所以有关二叉树的操作使用递归往往更容易理解和实现。

从定义也可以看出二叉树与一般树的区别主要是两点，一是每个结点的度最多为2；二是结点的子树有左右之分，不能随意调换，调换后又是一棵新的二叉树。

二、二叉树的形态

五种基本形态

从上面二叉树的递归定义可以看出，二叉树或为空，或为一个根结点加上两棵左右子树，因为两棵左右子树也是二叉树也可以为空，所以二叉树有5种基本形态：

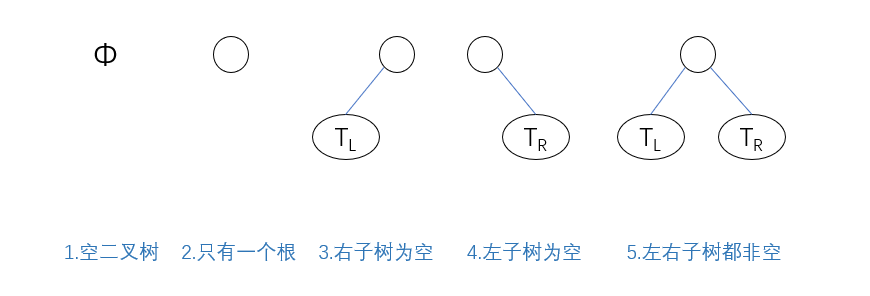
三种特殊形态

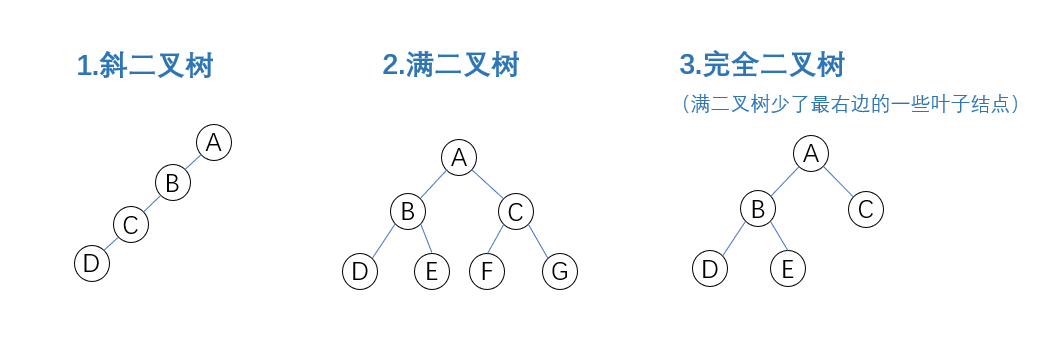
三、二叉树的性质

1. 任意二叉树第 $i$ 层最大结点数为$2^{i-1}。(i\ge 1)$
   归纳法证明。

2. 深度为 $k$ 的二叉树最大结点总数为$2^k-1。(k\ge 1)$
   证明：${\sum }_{i=1}^k{2}^{i-1}=2^k-1$

3. 对于任意二叉树，用$n_0,n_1,n_2$分别表示叶子结点，度为1的结点，度为2的结点的个数，则有关系式$n_0=n_2+1$。
   证明：总结点个数$n=n_0+n_1+n_2$；总结点中除根结点外，其余各结点都有一个分支进入，设$m$为分支总数，则有$n=m+1$，又因为这些分支都是由度为1或2的结点射出的，所以有$m=n_1+2n_2$，于是有$n=n_1+2n_2+1$；最后将关于$n$的两个关系式化简得证。

4. $n$个结点完全二叉树深度为$\lfloor lo{g}_{2}n\rfloor +1$。
   证明：设深度$k$，则有$2^{k-1}\le n<2^k\Rightarrow k-1\le lo{g}_{2}n<k\Rightarrow k=\lfloor lo{g}_{2}n\rfloor +1$

5. 性质5其实描述的是完全二叉树中父子结点间的逻辑对应关系。 假如对一棵完全二叉树的所有结点按层序遍历的顺序从1开始编号,对于编号后的结点$i$：
   （1）$i=1$时表示$i$是根结点；
   （2）$i>1$时：①$i$的父结点为$\lfloor \frac{i}{2}\rfloor$。②若$2i>n$，结点$i$无左孩子，且为叶子结点。③若$2i+1>n$，结点$i$无右孩子，可能为叶子结点。
   当然如果完全二叉树的根结点从0开始编号，那么上述关系就要相应修改一下。

四、二叉树的存储

存的目的是为了取，而取的关键在于如何通过父结点拿到它的左右子结点，不同存储方式围绕的核心也就是这。

顺序存储

使用一组地址连续的存储单元存储，例如数组。为了在存储结构中能得到父子结点之间的映射关系，二叉树中的结点必须按层次遍历的顺序存放。具体是：

• 对于完全二叉树，只需要自根结点起从上往下、从左往右依次存储。
• 对于非完全二叉树，首先将它变换为完全二叉树，空缺位置用某个特殊字符代替（比如#），然后仍按完全二叉树的存储方式存储。

假设将一棵二叉树按此方式存储到数组后，左子结点下标=2倍的父结点下标+1，右子节点下标=2倍的父结点下标+2（这里父子结点间的关系是基于根结点从0开始计算的）。若数组某个位置处值为#，代表此处对应的结点为空。

可以看出顺序存储非常适合存储接近完全二叉树类型的二叉树，对于一般二叉树有很大的空间浪费，所以对于一般二叉树，一般用下面这种链式存储。

链式存储

对每个结点，除数据域外再多增加左右两个指针域，分别指向该结点的左孩子和右孩子结点，再用一个头指针指向根结点。对应的存储结构：

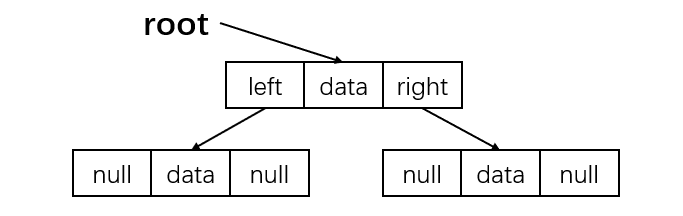
五、二叉树的创建与遍历（递归）

二叉树由三个基本单元组成：根结点，左子树，右子树，因此存在6种遍历顺序，若规定先左后右，则只有以下3种：
1.先序遍历
若二叉树为空，则空操作；否则：
（1）访问根结点
（2）先序遍历左子树
（3）先序遍历右子树

2.中序遍历
若二叉树为空，则空操作；否则：
（1）中序遍历左子树
（2）访问根结点
（3）中序遍历右子树

3.后序遍历
若二叉树为空，则空操作；否则：
（1）后序遍历左子树
（2）后序遍历右子树
（3）访问根结点

从上可以看出先中后其实是相对根结点来说。

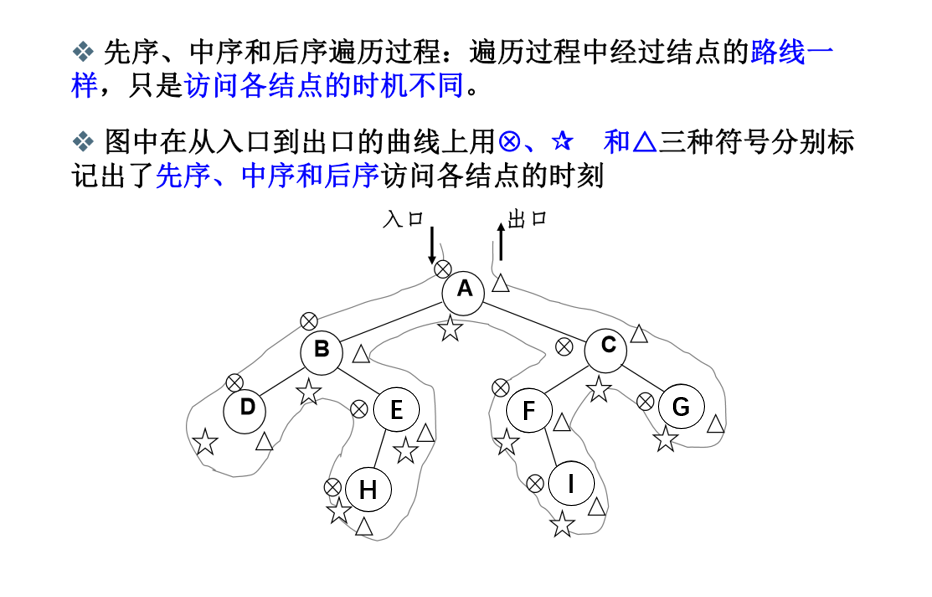
对于下面这棵二叉树，其遍历顺序：
先序：ABDEHCFIG
中序：DBHEAFICG
后序：DHEBIFGCA

下面是将以下二叉树的顺序存储[A,B,C,D,E,F,G,#,#,H,#,#,I]转换为链式存储的代码，结点不存在用字符#表示，并分别遍历。

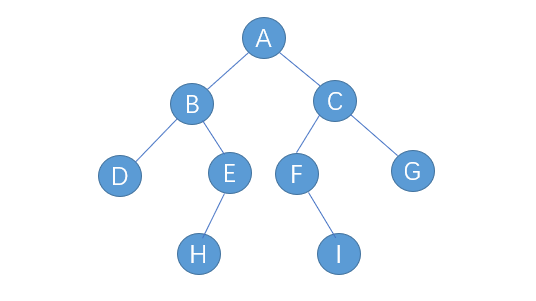
java代码

class TreeNode {
	char data;
	TreeNode lchild;								// 左子结点指针
	TreeNode rchild;								// 右子结点指针

	public TreeNode(char data) {
		this.data = data;
	}
}

public class BinaryTree {
	// 将二叉树的顺序存储变为链式存储
	public static TreeNode buildTree(char[] arr, int index) {
		TreeNode root = null;
		if (index < arr.length) {
			if (arr[index] == '#') {
				return null;
			}
			root = new TreeNode(arr[index]);
			root.lchild = buildTree(arr, 2 * index + 1);
			root.rchild = buildTree(arr, 2 * index + 2);
		}
		return root;
	}

	// 先序遍历
	public static void preOrderTraverse(TreeNode T) {
		if (T != null) {
			System.out.print(T.data);
			preOrderTraverse(T.lchild);
			preOrderTraverse(T.rchild);
		}
	}

	// 中序遍历
	public static void inOrderTraverse(TreeNode T) {
		if (T != null) {
			inOrderTraverse(T.lchild);
			System.out.print(T.data);
			inOrderTraverse(T.rchild);
		}
	}

	// 后序遍历
	public static void postOrderTraverse(TreeNode T) {
		if (T != null) {
			postOrderTraverse(T.lchild);
			postOrderTraverse(T.rchild);
			System.out.print(T.data);
		}
	}

	public static void main(String[] args) {
		char[] arr = { 'A', 'B', 'C', 'D', 'E', 'F', 'G', '#', '#', 'H', '#', '#', 'I' };
		TreeNode T = buildTree(arr, 0);

		System.out.print("先序遍历-->");
		preOrderTraverse(T);
		System.out.println();

		System.out.print("中序遍历-->");
		inOrderTraverse(T);
		System.out.println();

		System.out.print("后序遍历-->");
		postOrderTraverse(T);
		System.out.println();
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

仔细观察先序、中序、后序的结点访问顺序可以发现：

六、二叉树的非递归遍历

以上二叉树的创建及遍历都是通过递归实现，由三(三)、利用栈将递归转换为非递归可以将二叉树的递归遍历转换为非递归。

非递归的先序遍历

public static void preOrderWithoutRecursion(TreeNode T) {
	Stack<TreeNode> s = new Stack<>();
	while (T != null || !s.empty()) {
		if (T != null) {
			System.out.print(T.data);
			s.push(T);
			T = T.lchild;
		} else {
			T = s.pop();
			T = T.rchild;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13

非递归的中序遍历

public static void inOrderWithoutRecursion(TreeNode T) {
	Stack<TreeNode> s = new Stack<>();
	while (T != null || !s.empty()) {
		if (T != null) {
			s.push(T);
			T = T.lchild;
		} else {
			T = s.pop();
			System.out.print(T.data);
			T = T.rchild;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13

非递归的后序遍历

/*
 * 后序遍历要比先序中序遍历复杂一些，原因是需要判断上次访问的结点是位于左子树还是位于右子树。
 * 若位于左子树，需要跳过根结点并进入右子树，回头再访问根结点。
 * 若位于右子树，则直接访问根结点。
 */
public static void postOrderWithoutRecursion(TreeNode T) {
	Stack<TreeNode> s = new Stack<>();
	// 保存上次访问的结点
	TreeNode lastVisit = null;		
	// 首先一路压栈进入到左子树最左下端
	while (T != null) {
		s.push(T);
		T = T.lchild;
	}

	while (!s.empty()) {
		T = s.pop();
		// 一个根结点被访问的前提是：无右子树或右子树已被访问过
		if (T.rchild == null || T.rchild == lastVisit) {
			System.out.print(T.data);
			// 修改最近访问的结点
			lastVisit = T;
		} else {
			// 否则根结点再次入栈并直接进入到右子树
			s.push(T);
			T = T.rchild;
			// 并一路压栈进入到右子树的最左下端
			while (T != null) {
				s.push(T);
				T = T.lchild;
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

总结这种改写其实就是代码跟着思维走，模拟递归过程，用的仍然是递归的思想。

这里推荐一篇博客，作者将二叉树的非递归遍历讲解的透彻易懂，博客地址

七、二叉树的层序遍历（递归与非递归）

层次遍历是指从二叉树的根结点开始，按从上到下，从左到右的顺序遍历，也就是按从左往右的顺序先遍历第一层即根结点，再遍历第二层，…，直至最后一层。

还是上面的那棵二叉树，层序遍历顺序为：ABCDEFGHI。

递归

/*
 * 递归相比非递归优点就是思路清晰，代码易读，缺点是系统开销大。
 * 但是层序遍历的递归实现反而使算法更复杂。
 * 下面代码只提供层序遍历的一种递归思路，并不能算是真正意义上的递归。
 */
public static void levelOrderWithRecursion(TreeNode T) {
	if (T == null) {
		return;
	}
	
	// 获取树的深度
	int depth = depth(T);
	// 对每层循环遍历
	for (int i = 1; i <= depth; i++) {
		levelOrder(T, i);
	}
}

private static void levelOrder(TreeNode T, int level) {
	// if语句中去掉条件level<1不影响遍历结果，但对指定层遍历完成后仍然会继续递归调用，直到最下面结点的左右子结点为空结束递归
	if (T == null || level < 1) {
		return;
	}
	
	if (level == 1) {
		System.out.print(T.data);
	}
	levelOrder(T.lchild, level - 1);
	levelOrder(T.rchild, level - 1);
}

private static int depth(TreeNode T) {
	if (T == null) {
		return 0;
	}
		
	int l = depth(T.lchild);
	int r = depth(T.rchild);
	if (l > r) {
		return l + 1;
	} else {
		return r + 1;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

非递归

/*
 * 非递归遍历需要借助队列完成。
 * 因为对同一层的结点A和结点B，如果A在B的左边先被遍历，那么下一层中A的孩子也一定在B的孩子左边先被遍历。
 */
public static void levelOrderTraverse(TreeNode T) {
	if (T == null)
		return;
	
	Queue<TreeNode> q = new LinkedList<>();
	TreeNode node = null;
	// 首先根结点入队
	q.add(T);
	while (!q.isEmpty()) {
		// 队头出队
		node = q.remove();
		System.out.print(node.data);

		// 左右子结点入队
		if (node.lchild != null) {
			q.add(node.lchild);
		}
		if (node.rchild != null) {
			q.add(node.rchild);
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

八、四种遍历方式的时间和空间复杂度

四种遍历方式中，无论是递归还是非递归，二叉树的每个结点都只被访问一次，所以对于$n$个结点的二叉树，时间复杂度均为$O(n)$。

除层序遍历外的其它三种遍历方式，所需辅助空间为遍历过程中栈的最大容量，也就是二叉树的深度，所以空间复杂度与二叉树的形状有关。对于$n$个结点的二叉树，最好情况下是完全二叉树，空间复杂度$O(lo{g}_{2}n)$；最坏情况下对应斜二叉树，空间复杂度$O(n)$。层序遍历所需辅助空间为遍历过程中队列的最大长度，也就是二叉树的最大宽度$k$，所以空间复杂度$O(k)$。

九、根据遍历序列确定二叉树

（一）、根据先序、中序、后序遍历序列重建二叉树

从上面二叉树的遍历可以看出：如果二叉树中各结点值不同，那么先序、中序、以及后序遍历所得到的序列也是唯一。反过来，如果知道任意两种遍历序列，能否唯一确定这棵二叉树？

首先明确：只有先序中序，后序中序这两种组合可以唯一确定，先序后序不能。

如果知道的是先序中序，那么根据先序遍历先访问根结点的特点在中序序列中找到这个结点，该结点将中序序列分成两部分，左边是这个根结点的左子树中序序列，右边是这个根结点的右子树中序序列。根据这个序列，在先序序列中找到对应的左子序列和右子序列，根据先序遍历先访问根的特点又可以确定两个子序列的根结点，并根据这两个根结点可以将上次划分的两个中序子序列继续划分，如此下去，直到取尽先序序列中的结点时，便可得到对应的二叉树。

后序中序同理，区别是先序序列中第一个结点是根结点，而后序序列中最后一个结点是根结点。

先序和后序不能确定的原因在于不能确定根结点的左右子树。 比如先序序列AB，后序序列BA，根结点是A可以确定，但B是A的左子结点还是右子结点就确定不了了。

具体代码实现参考牛客网上《剑指Offer》中的一道题。查看

题目描述：输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

解题代码：

/*
 *下面代码来源原题下面的解答，思路很强！
 *用的是递归思想，每次将左右两棵子树当成新的子树进行处理，中序的左右子树开始结束索引很好找。
 *前序的左右子树的开始结束索引通过根结点与中序中左右子树的大小来计算。
 *然后递归求解，直到startPre>endPre||startIn>endIn说明子树整理完到。方法每次返回左子树和右子树的根结点。
 *事实上startPre>endPre||startIn>endIn两条件任选其一即可。为什么？仔细想想！
 */
public class ReBuildBinaryTree {	
	private static class TreeNode {
		int data;
		TreeNode lchild;
		TreeNode rchild;
		
		public TreeNode(int data) {
			super();
			this.data = data;
		}
	}

	public static TreeNode reBuildBinaryTree(int[] pre, int[] in) {
		TreeNode root = reBuildBinaryTree(pre, 0, pre.length - 1, in, 0, in.length - 1);
		return root;
	}

	private static TreeNode reBuildBinaryTree(int[] pre, int startPre, int endPre, int[] in, int startIn, int endIn) {
		// 两条件也可任选其一
		if (startPre > endPre || startIn > endIn)
			return null;

		TreeNode root = new TreeNode(pre[startPre]);
		for (int i = startIn; i <= endIn; i++) {
			if (in[i] == pre[startPre]) {
				// startPre+i-startIn=startPre+(i-startIn)，表示的意义是根结点索引+根结点的左子树结点总数，对应前序的左子树的结束索引。
				root.lchild = reBuildBinaryTree(pre, startPre + 1, startPre + i - startIn, in, startIn, i - 1);
				// i-startIn+startPre+1即在上面的基础上加1，前序左子树的结束索引+1=前序右子树的开始索引。
				root.rchild = reBuildBinaryTree(pre, i - startIn + startPre + 1, endPre, in, i + 1, endIn);
				break;
			}
		}
		return root;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

（二）、根据层序遍历序列重建二叉树（2023.11.5补）

刷题遇到（https://leetcode.cn/problems/binary-tree-right-side-view/description/），简单记录下，具体看代码，这里用python实现：

# 节点定义
class TreeNode:
    def __init__(self, val=None, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


# 层序遍历 -> 二叉树
def create_tree(arr: list, idx=0) -> TreeNode:
    # 这里如果不限制 arr[idx] is not None，则可构建一棵完全二叉树，对其层序遍历时可将输入参数arr原样输出而不忽略掉其中的None值
    if len(arr) - 1 >= idx and arr[idx] is not None:
        node = TreeNode(arr[idx])
        # 左右子节点位置与父节点位置下标关系分别为 2n+1 2n+2
        node.left = create_tree(arr, 2 * idx + 1)
        node.right = create_tree(arr, 2 * idx + 2)
        return node


# 二叉树 -> 层序遍历
def level_search(root):
    if root is None:
        return
    res = []
    from collections import deque
    q = deque(maxlen=100)
    q.append(root)
    while len(q) > 0:
        node = q.popleft()
        res.append(node.val)
        if node.left is not None:
            q.append(node.left)
        if node.right is not None:
            q.append(node.right)
    return res


if __name__ == '__main__':
    # 这里要求输入序列是按完全二叉树层序遍历顺序得到的，空缺位置用None代替
    arr = [1, 2, 3, None, 5, None, 4]
    root = create_tree(arr)
    res = level_search(root)
    print(res)  # [1, 2, 3, 5, 4]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

十、二叉树遍历算法的应用

在上面二叉树递归遍历的基础上，将具体的访问结点操作换成其它的某些操作就可以实现另外的一些功能。

1.按先序遍历的顺序建立二叉树

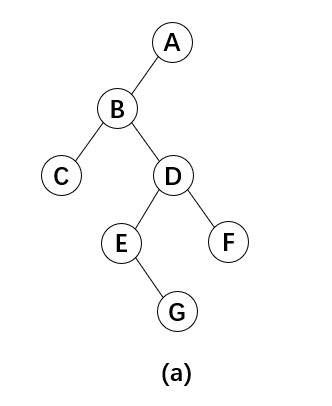
比如图(a)中的这棵二叉树，左子树或右子树不存在用字符#表示，对应的先序序列[ABC##DE#G##F###]，那么根据这个先序序列，也可以还原这棵二叉树。

要注意的是下面代码看似没有递归出口，其实不是，当输入的先序序列已经可以唯一确定二叉树的时候程序也会随之停止调用并结束。（写这块的时候花了一个晚上，原因是方法里的参数开始传的是先序数组和数组下标，然后递归的时候数组下标+1，忽视了逐层往里递归的时候虽然数组下标也逐层+1正确但最内部递归结束返回次内部往另一个方向递归的时候传入的数组下标还是该层数组下标没有+1时的值）

public static TreeNode build(Scanner sc) {
	char ch = (sc.nextLine().charAt(0));
	if (ch == '#') {
		return null;
	}
	
	TreeNode root = null;
	root = new TreeNode(ch);
	root.lchild = build(sc);
	root.rchild = build(sc);
	return root;
}
1
2
3
4
5
6
7
8
9
10
11
12

2.按先序遍历的顺序复制二叉树

public static TreeNode copy(TreeNode T) {
	if (T == null) {
		return null;
	}

	TreeNode newT = new TreeNode(T.data);
	newT.lchild = copy(T.lchild);
	newT.rchild = copy(T.rchild);
	return newT;
}
1
2
3
4
5
6
7
8
9
10

3.按后序遍历的顺序计算二叉树深度
二叉树深度为左右子树深度中的最大值+1，代码在二叉树递归的层序遍历中含有。

4.按先序遍历的顺序统计二叉树中结点个数
（1）统计所有结点个数
①当树为空时，结点个数为0；
②否则为根结点+根的左子树中结点个数+根的右子树中结点的个数。

public static int count(TreeNode T) {
	if (T == null)
		return 0;

	return count(T.lchild) + count(T.rchild) + 1;
}
1
2
3
4
5
6

（2）统计所有度为0也就是叶子结点的个数
①当树为空时，叶子结点个数为0；
②当某个结点的左右子树均为空时，说明该结点为叶子结点，返回1。
③否则表明该结点有左子树，或者有右子树，或者既有左子树又有右子树时，说明该结点不是叶子结点，因此叶结点个数等于左子树中叶子结点个数+右子树中叶子结点的个数。

public static int count(TreeNode T) {
	if (T == null)
		return 0;

	if (T.lchild == null && T.rchild == null)
		return 1;

	return count(T.lchild) + count(T.rchild);
}
1
2
3
4
5
6
7
8
9

（3）统计所有度为1的结点个数
①当树为空时，度为1的结点个数为0；
②当某个结点只有左子树或者只有右子树时，说明该结点是度为1的结点，返回1；
③否则表明该结点左右子树都存在，因此度为1的结点个数=左子树中度为1的结点个数+右子树中度为1的结点个数。

public static int count(TreeNode T) {
	if (T == null)
		return 0;
	
	// 条件中可以不用括号，短路与“&&”的优先级高于短路或“||”。
	if ((T.lchild == null && T.rchild != null) || (T.lchild != null && T.rchild == null))
		return 1;

	return count(T.lchild) + count(T.rchild);
}
1
2
3
4
5
6
7
8
9
10

（4）统计所有度为2也就是满结点的个数
①当树为空时，度为2的结点个数为0；
②当某个结点左子树和右子树都存在时，说明该结点是度为2的结点，返回1；
③否则表明该结点存在且不是满结点，因此满结点个数=该结点左子树中的满结点个数+该结点右子树中的满结点个数（必有一子树不存在，但会返回0不影响结果）。

public static int count(TreeNode T) {
	if (T == null)
		return 0;

	if (T.lchild != null && T.rchild != null)
		return count(T.lchild) + count(T.rchild) + 1;

	return count(T.lchild) + count(T.rchild);
}
1
2
3
4
5
6
7
8
9