- 1Ubuntu+Systemd服务+实现开机自启/关机启动脚本
- 2小白的最强保姆教学:PicGo + gitee +Typora免费搭建属于个人的图床工具_picgo+csdn
- 3计算机毕业设计 SSM共享充电宝管理系统(源码+论文)_共享充电宝数据库系统设计
- 4PySpark实战指南:大数据处理与分析的终极指南_pyspark大数据分析实战
- 5【转载】发生「null参数报错」的正确解决方法 | 亲子课堂 第 13 课_无限蜂大背包null报错
- 6ToDesk企业版使用测试:破解企业远程办公难题,更安全更高效_todesk部署码(1)
- 7在gazebo里搭建一个livox mid360 + 惯导仿真平台测试 FAST-LIO2_mid360 gazebo
- 8Python+Django+Mysql+SimpleUI搭建后端用户管理系统(非常详细,每一步都清晰,列举了里面所有使用的方法属性)_用python做一个管理系统
- 9mysql sqlalchemy 索引_python – 在SQLAlchemy中设置索引限制
- 10探索 Simple Netty 源码:轻松理解高性能网络编程
大规模 Transformer 模型 8 比特矩阵乘简介 - 基于 Hugging Face Transformers、Accelerate 以及 bitsandbytes
赞
踩
文章目录
本文转载整理自:大规模 Transformer 模型 8 比特矩阵乘简介 - 基于 Hugging Face Transformers、Accelerate 以及 bitsandbytes ( 2022年8月17日)
https://huggingface.co/blog/zh/hf-bitsandbytes-integration
一、引言
语言模型一直在变大。截至撰写本文时,PaLM 有 5400 亿参数,OPT、GPT-3 和 BLOOM 有大约 1760 亿参数,而且我们仍在继续朝着更大的模型发展。
下图总结了最近的一些语言模型的尺寸。

由于这些模型很大,因此它们很难在一般的设备上运行。
举个例子,仅推理 BLOOM-176B 模型,你就需要 8 个 80GB A100 GPU (每个约 15,000 美元)。
而如果要微调 BLOOM-176B 的话,你需要 72 个这样的 GPU!更大的模型,如 PaLM,还需要更多资源。
由于这些庞大的模型需要大量 GPU 才能运行,因此我们需要找到降低资源需求而同时保持模型性能的方法。
目前已有一些试图缩小模型尺寸的技术,比如你可能听说过的量化和蒸馏等技术。
完成 BLOOM-176B 的训练后,Hugging Face 和 BigScience 一直在寻找能让这个大模型更容易在更少的 GPU 上运行的方法。
通过我们的 BigScience 社区,我们了解到一些有关 Int8 推理的研究,它不会降低大模型的预测性能,而且可以将大模型的内存占用量减少 2 倍。
很快我们就开始合作进行这项研究,最终将其完全整合到 Hugging Face transformers中。
本文我们将详述我们集成在 Hugging Face 中的 LLM.int8() 方案,它适用于所有 Hugging Face 模型。
如果你想了解更多研究细节,可以阅读我们的论文 LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale。
本文将主要介绍 LLM.int8() 量化技术,讨论将其纳入 transformers 库的过程中经历的困难,并对后续工作进行了计划。
在这里,你将了解到究竟是什么让一个大模型占用这么多内存?是什么让 BLOOM 占用了 350GB 内存?我们先从一些基础知识开始,慢慢展开。
二、机器学习中常用的数据类型
我们从理解不同浮点数据类型开始,这些数据类型在机器学习中也被称为“精度”。
模型的大小由其参数量及其精度决定,精度通常为 float32、float16 或 bfloat16 之一 (下图来源)。
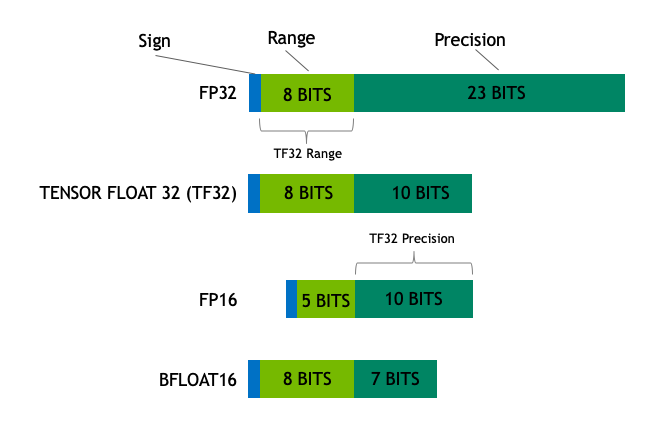
Float32 (FP32) 是标准的 IEEE 32 位浮点表示。
使用该数据类型,可以表示大范围的浮点数。
在 FP32 中,为“指数”保留了 8 位,为“尾数”保留了 23 位,为符号保留了 1 位。
因为是标准数据类型,所以大部分硬件都支持 FP32 运算指令。
而在 Float16 (FP16) 数据类型中,指数保留 5 位,尾数保留 10 位。
这使得 FP16 数字的数值范围远低于 FP32。
因此 FP16 存在上溢 (当用于表示非常大的数时) 和下溢 (当用于表示非常小的数时) 的风险。
例如,当你执行 10k * 10k 时,最终结果应为 100M,FP16 无法表示该数,因为 FP16 能表示的最大数是 64k。
因此你最终会得到 NaN (Not a Number,不是数字),在神经网络的计算中,因为计算是按层和 batch 顺序进行的,因此一旦出现 NaN,之前的所有计算就全毁了。
一般情况下,我们可以通过缩放损失 (loss scaling) 来缓解这个问题,但该方法并非总能奏效。
于是我们发明了一种新格式 Bfloat16 (BF16) 来规避这些限制。
BF16 为指数保留了 8 位 (与 FP32 相同),为小数保留了 7 位。
这意味着使用 BF16 我们可以保留与 FP32 相同的动态范围。但是相对于 FP16,我们损失了 3 位精度。
因此,在使用 BF16 精度时,大数值绝对没有问题,但是精度会比 FP16 差。
在 Ampere 架构中,NVIDIA 还引入了 TensorFloat-32(TF32) 精度格式,它使用 19 位表示,结合了 BF16 的范围和 FP16 的精度。
目前,它仅在某些操作的内部使用 [译者注: 即 TF32 是一个计算数据类型而不是存储数据类型]。
在机器学习术语中,FP32 称为全精度 (4 字节),而 BF16 和 FP16 称为半精度 (2 字节)。
除此以外,还有 Int8 (INT8) 数据类型,它是一个 8 位的整型数据表示,可以存储
2
8
2^8
28 个不同的值 (对于有符号整数,区间为 [-128, 127],而对于无符号整数,区间为 [0, 255])。
虽然理想情况下训练和推理都应该在 FP32 中完成,但 FP32 比 FP16/BF16 慢两倍,因此实践中常常使用混合精度方法,其中,使用 FP32 权重作为精确的 “主权重 (master weight)”,而使用 FP16/BF16 权重进行前向和后向传播计算以提高训练速度,最后在梯度更新阶段再使用 FP16/BF16 梯度更新 FP32 主权重。
在训练期间,主权重始终为 FP32。
而在实践中,在推理时,半精度权重通常能提供与 FP32 相似的精度 —— 因为只有在模型梯度更新时才需要精确的 FP32 权重。
这意味着在推理时我们可以使用半精度权重,这样我们仅需一半 GPU 显存就能获得相同的结果。
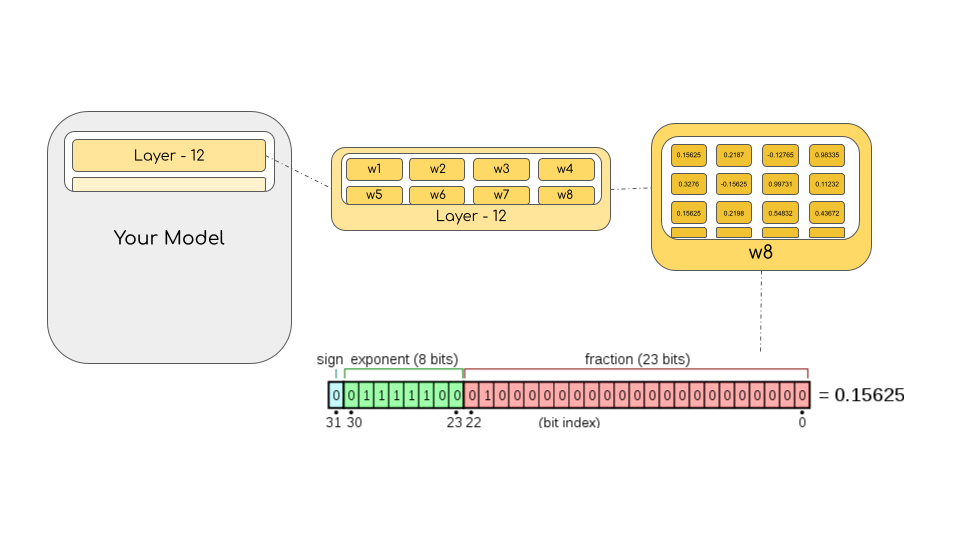
以字节为单位计算模型大小时,需要将参数量乘以所选精度的大小 (以字节为单位)。
例如,如果我们使用 BLOOM-176B 模型的 Bfloat16 版本,其大小就应为 $ 176 \times 10^{9} \times 2 字节 = 352GB $ !如前所述,这个大小需要多个 GPU 才能装得下,这是一个相当大的挑战。
但是,如果我们可以使用另外的数据类型来用更少的内存存储这些权重呢?深度学习社区已广泛使用的方法是量化。
三、模型量化简介
通过实验,我们发现不使用 4 字节 FP32 精度转而使用 2 字节 BF16/FP16 半精度可以获得几乎相同的推理结果,同时模型大小会减半。
这促使我们想进一步削减内存,但随着我们使用更低的精度,推理结果的质量也开始急剧下降。
为了解决这个问题,我们引入了 8 位量化。
仅用四分之一精度,因此模型大小也仅需 1/4!但这次,我们不能简单地丢弃另一半位宽了。
基本上讲,量化过程是从一种数据类型“舍入”到另一种数据类型。
举个例子,如果一种数据类型的范围为 0..9,而另一种数据类型的范围为 0..4,则第一种数据类型中的值 4 将舍入为第二种数据类型中的 2 。
但是,如果在第一种数据类型中有值 3,它介于第二种数据类型的 1 和 2 之间,那么我们通常会四舍五入为 2。
也就是说,第一种数据类型的值 4 和 3在第二种数据类型中具有相同的值 2。
这充分表明量化是一个有噪过程,会导致信息丢失,是一种有损压缩。
两种最常见的 8 位量化技术是零点量化 (zero-point quantization) 和最大绝对值 (absolute maximum quantization,absmax) 量化。
它们都将浮点值映射为更紧凑的 Int8 (1 字节) 值。
这些方法的第一步都是用量化常数对输入进行归一化缩放。
在零点量化中,如果我的数值范围是 -1.0…1.0,我想量化到 -127…127,我需要先缩放 127倍,然后四舍五入到 8 位精度。
要恢复原始值,我需要将 Int8 值除以相同的量化因子 127。
在这个例子中,值 0.3 将缩放为 0.3*127 = 38.1。
四舍五入后得到值 38。
恢复时,我们会得到 38/127=0.2992 —— 因此最终会有 0.008 的量化误差。
这些看似微小的误差在沿着模型各层传播时往往会累积和增长,从而导致最终的精度下降。
译者注: 这个例子举得不好,因为浮点范围和整型范围都是对称的,所以不存在零点调整了,而零点调整是零点量化中最能体现其命名原因的部分。
简而言之,零点量化分为两步,第一步值域映射,即通过缩放将原始的数值范围映射为量化后的数值范围; 第二步零点调整,即通过平移将映射后的数据的最小值对齐为目标值域的最小值
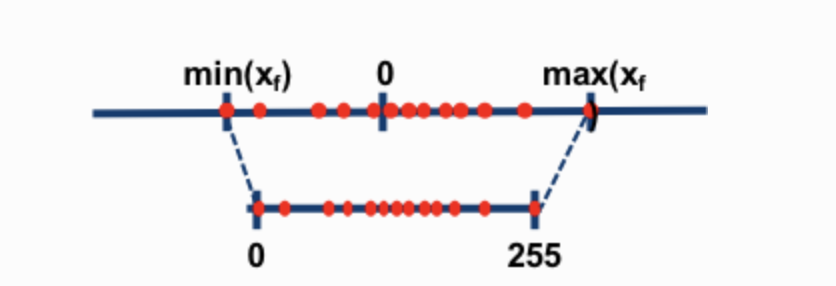
(图源)
现在我们再看下 absmax 量化的细节。
要计算 absmax 量化中 fp16 数与其对应的 int8 数之间的映射,你必须先除以张量的最大绝对值,然后再乘以数据类型的最大可表示值。
例如,假设你要用 absmax 对向量 [1.2, -0.5, -4.3, 1.2, -3.1, 0.8, 2.4, 5.4] 进行量化。
首先需要计算该向量元素的最大绝对值,在本例中为 5.4。
Int8 的范围为 [-127, 127],因此我们将 127 除以 5.4,得到缩放因子 23.5。
最后,将原始向量乘以缩放因子得到最终的量化向量 [28, -12, -101, 28, -73, 19, 56, 127]。
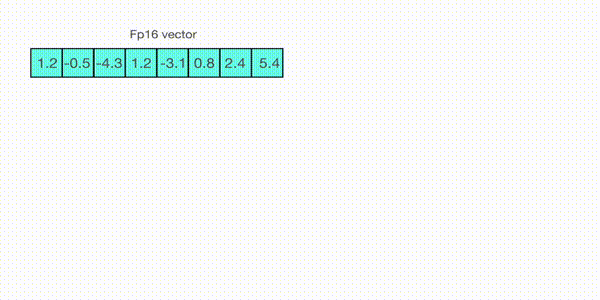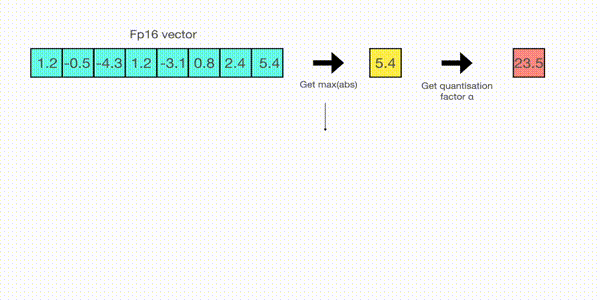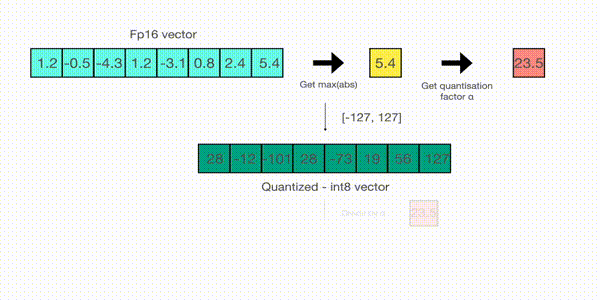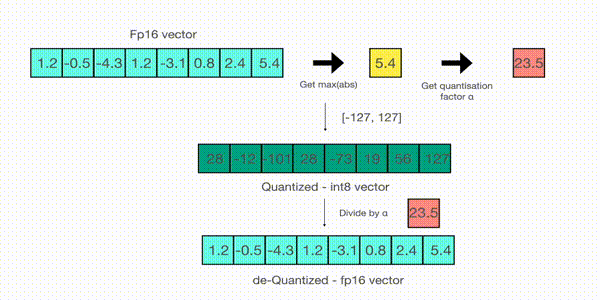
要恢复原向量,可以将 int8 量化值除以缩放因子,但由于上面的过程是“四舍五入”的,我们将丢失一些精度。
[
对于无符号 Int8,我们可以先减去最小值然后再用最大绝对值来缩放,这与零点量化的做法相似。
其做法也与最小 - 最大缩放 (min-max scaling) 类似,但后者在缩放时会额外保证输入中的 0 始终映射到一个整数,从而保证 0 的量化是无误差的。
当进行矩阵乘法时,我们可以通过组合各种技巧,例如逐行或逐向量量化,来获取更精确的结果。
举个例子,对矩阵乘法
A
×
B
=
C
A \times B=C
A×B=C,我们不会直接使用常规量化方式,即用整个张量的最大绝对值对张量进行归一化,而会转而使用向量量化方法,找到 A 的每一行和 B 的每一列的最大绝对值,然后逐行或逐列归一化 A 和 B 。
最后将 A 与 B 相乘得到 C。
最后,我们再计算与 A 和 B 的最大绝对值向量的外积,并将此与 C 求哈达玛积来反量化回 FP16。
有关此技术的更多详细信息可以参考 LLM.int8() 论文 或 Tim 的博客上的 关于量化和涌现特征的博文。
虽然这些基本技术能够帮助我们量化深度学习模型,但它们通常会导致大模型准确性的下降。
我们集成到 Hugging Face Transformers 和 Accelerate 库中的 LLM.int8() 是第一个适用于大模型 (如 BLOOM-176B) 且不会降低准确性的量化技术。
四、简要总结 LLM.int8(): 大语言模型的零退化矩阵乘法
在 LLM.int8() 中,我们已经证明理解 transformer 模型表现出的与模型规模相关的涌现特性对于理解为什么传统量化对大模型失效至关重要。
我们证明性能下降是由离群特征 (outlier feature) 引起的,下一节我们会详细解释。
LLM.int8() 算法本身如下。
本质上,LLM.int8() 通过三个步骤完成矩阵乘法计算:
-
从输入的隐含状态中,按列提取异常值 (即大于某个阈值的值)。
-
对 FP16 离群值矩阵和 Int8 非离群值矩阵分别作矩阵乘法。
-
反量化非离群值的矩阵乘结果并其与离群值矩阵乘结果相加,获得最终的 FP16 结果。
该过程可以总结为如下动画:
离群特征的重要性
超出某个分布范围的值通常称为离群值。
离群值检测已得到广泛应用,在很多文献中也有涉及,且获取特征的先验分布对离群值检测任务很有助益。
更具体地说,我们观察到对于参数量大于 6B 的 transformer 模型,经典的量化方法会失效。
虽然离群值特征也存在于较小的模型中,但在大于 6B 的 transformer 模型中,我们观察到几乎每层都会出现超出特定阈值的离群点,而且这些离群点呈现出一定的系统性模式。
有关该现象的更多详细信息,请参阅 LLM.int8() 论文 和 涌现特征的博文。
如前所述,8 位精度的动态范围极其有限,因此量化具有多个大值的向量会产生严重误差。
此外,由于 transformer 架构的固有特性,它会将所有元素互相关联起来,这样的话,这些误差在传播几层后往往会混杂在一起。
因此,我们发明了混合精度分解的方法,以对此类极端离群值进行有效量化。
接下来我们对此方法进行讨论。
MatMul 内部
计算隐含状态后,我们使用自定义阈值提取离群值,并将矩阵分解为两部分,如上所述。
我们发现,以这种方式提取所有幅度大于等于 6 的离群值可以完全恢复推理精度。
离群值部分使用 FP16 表示,因此它是一个经典的矩阵乘法,而 8 位矩阵乘法是通过使用向量量化将权重和隐含状态分别量化为 8 位精度 - 即按行量化权重矩阵,并按列量化隐含状态,然后再进行相应向量乘加操作。
最后,将结果反量化至半精度,以便与第一个矩阵乘法的结果相加。
0 退化是什么意思?
我们如何正确评估该方法是否会对性能造成下降?使用 8 位模型时,我们的生成质量损失了多少?
我们使用 lm-eval-harness 在 8 位和原始模型上运行了几个常见的基准测试,结果如下。
对 OPT-175B 模型:
| 测试基准 | - | - | - | - | 差值 |
|---|---|---|---|---|---|
| 测试基准名 | 指标 | 指标值 - int8 | 指标值 - fp16 | 标准差 - fp16 | - |
| hellaswag | acc_norm | 0.7849 | 0.7849 | 0.0041 | 0 |
| hellaswag | acc | 0.5921 | 0.5931 | 0.0049 | 0.001 |
| piqa | acc | 0.7965 | 0.7959 | 0.0094 | 0.0006 |
| piqa | acc_norm | 0.8101 | 0.8107 | 0.0091 | 0.0006 |
| lambada | ppl | 3.0142 | 3.0152 | 0.0552 | 0.001 |
| lambada | acc | 0.7464 | 0.7466 | 0.0061 | 0.0002 |
| winogrande | acc | 0.7174 | 0.7245 | 0.0125 | 0.0071 |
对 BLOOM-176 模型:
| 测试基准 | - | - | - | - | 差值 |
|---|---|---|---|---|---|
| 测试基准名 | 指标 | 指标值 - int8 | 指标值 - fp16 | 标准差 - fp16 | - |
| hellaswag | acc_norm | 0.7274 | 0.7303 | 0.0044 | 0.0029 |
| hellaswag | acc | 0.5563 | 0.5584 | 0.005 | 0.0021 |
| piqa | acc | 0.7835 | 0.7884 | 0.0095 | 0.0049 |
| piqa | acc_norm | 0.7922 | 0.7911 | 0.0095 | 0.0011 |
| lambada | ppl | 3.9191 | 3.931 | 0.0846 | 0.0119 |
| lambada | acc | 0.6808 | 0.6718 | 0.0065 | 0.009 |
| winogrande | acc | 0.7048 | 0.7048 | 0.0128 | 0 |
我们切实地看到上述这些模型的性能下降为 0,因为指标的绝对差异均低于原始模型的标准误差 (BLOOM-int8 除外,它在 lambada 上略好于原始模型)。
如果想要知道 LLM.int8() 与当前其他先进方法的更详细的性能比较,请查看 论文!
比原始模型更快吗?
LLM.int8() 方法的主要目的是在不降低性能的情况下降低大模型的应用门槛。
但如果速度非常慢,该方法用处也不会很大。
所以我们对多个模型的生成速度进行了基准测试。
我们发现使用了 LLM.int8() 的 BLOOM-176B 比 FP16 版本慢了大约 15% 到 23% —— 这应该是完全可以接受的。
我们发现较小模型 (如 T5-3B 和 T5-11B) 的降速幅度更大。
我们还在努力优化这些小模型的推理速度。
在一天之内,我们可以将 T5-3B 的每词元推理延迟从 312 毫秒降低到 173 毫秒,将 T5-11B 从 45 毫秒降低到 25 毫秒。
此外,我们 已经找到原因,在即将发布的版本中,LLM.int8() 在小模型上的推理速度可能会更快。
下表列出了当前版本的一些性能数据。
| 精度 | 参数量 | 硬件 | 每词元延迟 (单位: 毫秒,batch size: 1) | 每词元延迟 (单位: 毫秒,batch size: 8) | 每词元延迟 (单位: 毫秒,batch size: 32) |
|---|---|---|---|---|---|
| bf16 | 176B | 8xA100 80GB | 239 | 32 | 9.9 |
| int8 | 176B | 4xA100 80GB | 282 | 37.5 | 10.2 |
| bf16 | 176B | 14xA100 40GB | 285 | 36.5 | 10.4 |
| int8 | 176B | 5xA100 40GB | 367 | 46.4 | oom |
| fp16 | 11B | 2xT4 15GB | 11.7 | 1.7 | 0.5 |
| int8 | 11B | 1xT4 15GB | 43.5 | 5.3 | 1.3 |
| fp32 | 3B | 2xT4 15GB | 45 | 7.2 | 3.1 |
| int8 | 3B | 1xT4 15GB | 312 | 39.1 | 10.2 |
上表中的 3 个模型分别为 BLOOM-176B、T5-11B 和 T5-3B。
五、Hugging Face transformers 集成细节
接下来让我们讨论在 Hugging Face transformers 集成该方法的细节,向你展示常见的用法及在使用过程中可能遇到的常见问题。
1、用法
所有的操作都集成在 Linear8bitLt 模块中,你可以轻松地从 bitsandbytes 库中导入它。
它是 torch.nn.modules 的子类,你可以仿照下述代码轻松地将其应用到自己的模型中。
下面以使用 bitsandbytes 将一个小模型转换为 int8 为例,并给出相应的步骤。
(1) 首先导入模块,如下。
import torch
import torch.nn as nn
import bitsandbytes as bnb
from bnb.nn import Linear8bitLt
- 1
- 2
- 3
- 4
- 5
(2) 然后就可以定义自己的模型了。
请注意,我们支持将任何精度的 checkpoint 或模型转换为 8 位 (FP16、BF16 或 FP32),但目前,仅当模型的输入张量数据类型为 FP16 时,我们的 Int8 模块才能工作。
因此,这里我们称模型为 fp16 模型。
fp16_model = nn.Sequential(
nn.Linear(64, 64),
nn.Linear(64, 64)
)
- 1
- 2
- 3
- 4
(3) 假设你已经在你的数据集和任务上训完了你的模型!现在需要保存模型:
[... train the model ...]
torch.save(fp16_model.state_dict(), "model.pt")
- 1
- 2
(4) 至此,state_dict 已保存,我们需要定义一个 int8 模型:
int8_model = nn.Sequential(
Linear8bitLt(64, 64, has_fp16_weights=False),
Linear8bitLt(64, 64, has_fp16_weights=False)
)
- 1
- 2
- 3
- 4
此处标志变量 has_fp16_weights 非常重要。
默认情况下,它设置为 True,用于在训练时使能 Int8/FP16 混合精度。
但是,因为在推理中我们对内存节省更感兴趣,因此我们需要设置 has_fp16_weights=False。
(5) 现在加载 8 位模型!
int8_model.load_state_dict(torch.load("model.pt"))
int8_model = int8_model.to(0) # 量化发生在此处
- 1
- 2
请注意,一旦将模型的设备设置为 GPU,量化过程就会在第二行代码中完成。
如果在调用 .to 函数之前打印 int8_model[0].weight,你会看到:
int8_model[0].weight
Parameter containing:
tensor([[ 0.0031, -0.0438, 0.0494, ..., -0.0046, -0.0410, 0.0436],
[-0.1013, 0.0394, 0.0787, ..., 0.0986, 0.0595, 0.0162],
[-0.0859, -0.1227, -0.1209, ..., 0.1158, 0.0186, -0.0530],
...,
[ 0.0804, 0.0725, 0.0638, ..., -0.0487, -0.0524, -0.1076],
[-0.0200, -0.0406, 0.0663, ..., 0.0123, 0.0551, -0.0121],
[-0.0041, 0.0865, -0.0013, ..., -0.0427, -0.0764, 0.1189]],
dtype=torch.float16)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
而如果你在第二行之后打印它,你会看到:
int8_model[0].weight
Parameter containing:
tensor([[ 3, -47, 54, ..., -5, -44, 47],
[-104, 40, 81, ..., 101, 61, 17],
[ -89, -127, -125, ..., 120, 19, -55],
...,
[ 82, 74, 65, ..., -49, -53, -109],
[ -21, -42, 68, ..., 13, 57, -12],
[ -4, 88, -1, ..., -43, -78, 121]],
device='cuda:0', dtype=torch.int8, requires_grad=True)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
正如我们在前面部分解释量化方法时所讲,权重值被“截断”了。
此外,这些值的分布看上去在 [-127, 127] 之间。
你可能还想知道如何获取 FP16 权重以便在 FP16 中执行离群值的矩阵乘?很简单:
(int8_model[0].weight.CB * int8_model[0].weight.SCB) / 127
- 1
你会看到:
tensor([[ 0.0028, -0.0459, 0.0522, ..., -0.0049, -0.0428, 0.0462],
[-0.0960, 0.0391, 0.0782, ..., 0.0994, 0.0593, 0.0167],
[-0.0822, -0.1240, -0.1207, ..., 0.1181, 0.0185, -0.0541],
...,
[ 0.0757, 0.0723, 0.0628, ..., -0.0482, -0.0516, -0.1072],
[-0.0194, -0.0410, 0.0657, ..., 0.0128, 0.0554, -0.0118],
[-0.0037, 0.0859, -0.0010, ..., -0.0423, -0.0759, 0.1190]],
device='cuda:0')
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
这跟第一次打印的原始 FP16 值很接近!
(6)现在你只需将输入推给正确的 GPU 并确保输入数据类型是 FP16 的,你就可以使用该模型进行推理了:
input_ = torch.randn(64, dtype=torch.float16)
hidden_states = int8_model(input_.to(torch.device('cuda', 0)))
- 1
- 2
你可以查看 示例脚本,获取完整的示例代码!
多说一句, Linear8bitLt 与 nn.Linear 模块略有不同,主要在 Linear8bitLt 的参数属于 bnb.nn.Int8Params 类而不是 nn.Parameter 类。
稍后你会看到这给我们带来了一些小麻烦!
现在我们开始了解如何将其集成到 transformers 库中!
2、accelerate 足矣
在处理大模型时, accelerate 库包含许多有用的工具。
init_empty_weights 方法特别有用,因为任何模型,无论大小,都可以在此方法的上下文 (context) 内进行初始化,而无需为模型权重分配任何内存。
import torch.nn as nn
from accelerate import init_empty_weights
with init_empty_weights():
model = nn.Sequential([nn.Linear(100000, 100000) for _ in range(1000)]) # This will take ~0 RAM!
- 1
- 2
- 3
- 4
- 5
初始化过的模型将放在 PyTorch 的 meta 设备上,这是一种用于表征向量的形状和数据类型而无需实际的内存分配的超酷的底层机制。
最初,我们在 .from_pretrained 函数内部调用 init_empty_weights,并将所有参数重载为 torch.nn.Parameter。
这不是我们想要的,因为在我们的情况中,我们希望为 Linear8bitLt 模块保留 Int8Params 类,如上所述。
我们最后成功使用 此 PR 修复了该问题,它将下述代码:
module._parameters[name] = nn.Parameter(module._parameters[name].to(torch.device("meta")))
- 1
修改成:
param_cls = type(module._parameters[name])
kwargs = module._parameters[name].__dict__
module._parameters[name] = param_cls(module._parameters[name].to(torch.device("meta")), **kwargs)
- 1
- 2
- 3
现在这个问题已经解决了,我们可以轻松地在一个自定义函数中利用这个上下文管理器将所有 nn.Linear 模块替换为 bnb.nn.Linear8bitLt 而无需占用内存!
def replace_8bit_linear(model, threshold=6.0, module_to_not_convert="lm_head"):
for name, module in model.named_children():
if len(list(module.children())) > 0:
replace_8bit_linear(module, threshold, module_to_not_convert)
if isinstance(module, nn.Linear) and name != module_to_not_convert:
with init_empty_weights():
model._modules[name] = bnb.nn.Linear8bitLt(
module.in_features,
module.out_features,
module.bias is not None,
has_fp16_weights=False,
threshold=threshold,
)
return model
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
此函数递归地将 meta 设备上初始化的给定模型的所有 nn.Linear 层替换为 Linear8bitLt 模块。
这里,必须将 has_fp16_weights 属性设置为 False,以便直接将权重加载为 Int8,并同时加载其量化统计信息。
我们放弃了对某些模块 (这里时 lm_head) 进行替换,因为我们希望保持输出层的原始精度以获得更精确、更稳定的结果。
但还没完!上面的函数在 init_empty_weights 上下文管理器中执行,这意味着新模型将仍在 meta 设备中。
对于在此上下文管理器中初始化的模型, accelerate 将手动加载每个模块的参数并将它们拷贝到正确的设备上。
因此在 bitsandbytes 中,设置 Linear8bitLt 模块的设备是至关重要的一步 (感兴趣的读者可以查看 此代码),正如你在我们上面提供的脚本中所见。
而且,第二次调用量化过程时会失败!我们必须想出一个与 accelerate 的 set_module_tensor_to_device 函数相应的实现 (称为 set_module_8bit_tensor_to_device),以确保我们不会调用两次量化。
我们将在下面的部分中详细讨论这个问题!
3、在 accelerate 设置设备要当心
这方面,我们对 accelerate 库进行了精巧的修改,以取得平衡!
在模型被加载且设置到正确的设备上后,有时你仍需调用 set_module_tensor_to_device 以便向所有设备分派加了 hook 的模型。
该操作在用户调用 accelerate 的 dispatch_model 函数时会被触发,这意味着我们有可能多次调用 .to,我们需要避免该行为。
我们通过两个 PR 实现了目的,这里 的第一个 PR 破坏了一些测试,但 这个 PR 成功修复了所有问题!
4、总结
因此,最终我们完成了:
-
使用正确的模块在
meta设备上初始化模型。 -
不重不漏地对目标 GPU 逐一设置参数,确保不要对同一个 GPU 重复设置!
-
将新加的参数变量更新到所有需要的地方,并添加好文档。
-
添加高覆盖度的测试! 你可以从 此处 查看更多关于测试的详细信息。
知易行难,在此过程中,我们经历了许多艰难的调试局,其中很多跟 CUDA 核函数有关!
总而言之,这次集成的过程充满了冒险和趣味; 从深入研究并对不同的库做一些“手术”,到整合一切并最终使其发挥作用,每一步都充满挑战!
现在,我们看看如何在 transformers 中成功使用它并从中获益!
六、如何在 transformers 中使用它
硬件要求
CPU 不支持 8 位张量核心 [译者注: Intel 最新的 Sapphire Rapids CPU 已支持 8 位张量指令集: AMX]。
bitsandbytes 可以在支持 8 位张量核心的硬件上运行,这些硬件有 Turing 和 Ampere GPU (RTX 20s、RTX 30s、A40-A100、T4+)。
例如,Google Colab GPU 通常是 NVIDIA T4 GPU,而最新的 T4 是支持 8 位张量核心的。
我们后面的演示将会基于 Google Colab!
安装
使用以下命令安装最新版本的库 (确保你的 python>=3.8)。
pip install accelerate
pip install bitsandbytes
pip install git+https://github.com/huggingface/transformers.git
- 1
- 2
- 3
演示示例 - 在 Google Colab 上运行 T5 11B
以下是运行 T5-11B 的演示。
T5-11B 模型的 checkpoint 精度为 FP32,需要 42GB 内存,Google Colab 里跑不动。
使用我们的 8 位模块,它仅需 11GB 内存,因此能轻易跑通:
或者,你还可以看看下面这个使用 8 位 BLOOM-3B 模型进行推理的演示!
七、影响范围
我们认为,该方法让超大模型不再是阳春白雪,而是人人皆可触及。
在不降低性能的情况下,它使拥有较少算力的用户能够使用以前无法使用的模型。
我们已经发现了几个可以在继续改进的领域,以使该方法对大模型更友好!
较小模型的推理加速
正如我们在 [基准测试部分](# 比原始模型更快吗?) 中看到的那样,我们可以将小模型 (<=6B 参数) 的运行速度提高近 2 倍。
然而,虽然推理速度对于像 BLOOM-176B 这样的大模型来说比较稳定,但对小模型而言仍有改进的余地。
我们已经定位到了问题并有希望恢复与 FP16 相同的性能,甚至还可能会有小幅加速。
我们将在接下来的几周内合入这些改进。
支持 Kepler GPU (GTX 1080 等)
虽然我们只支持过去四年的所有 GPU,但现实是某些旧的 GPU (如 GTX 1080) 现在仍然被大量使用。
虽然这些 GPU 没有 Int8 张量核心,但它们有 Int8 向量单元 (一种“弱”张量核心)。
因此,这些 GPU 也可以体验 Int8 加速。
然而,它需要一个完全不同的软件栈来优化推理速度。
虽然我们确实计划集成对 Kepler GPU 的支持以使 LLM.int8() 的应用更广泛,但由于其复杂性,实现这一目标需要一些时间。
在 Hub 上保存 8 位 checkpoint
目前 8 位模型无法直接加载被推送到 Hub 上的 8 位 checkpoint。
这是因为模型计算所需的统计数据 (还记得上文提到的 weight.CB 和 weight.SCB 吗?) 目前没有存储在 state_dict 中,而且 state_dict 的设计也未考虑这一信息的存储,同时 Linear8bitLt 模块也还尚未支持该特性。
但我们认为保存它并将其推送到 Hub 可能有助于提高模型的可访问性。
CPU 的支持
正如本文开头所述,CPU 设备不支持 8 位张量核。
然而,我们能克服它吗?在 CPU 上运行此模块可以显著提高可用性和可访问性。
[译者注: 如上文,最新的 Intel CPU 已支持 8 位张量核]
扩展至其他模态
目前,大模型以语言模型为主。
在超大视觉、音频和多模态模型上应用这种方法可能会很有意思,因为随着这些模型在未来几年变得越来越多,它们的易用性也会越来越重要。
2024-04-23(二)




