强化学习策略梯度推导_强化学习 推导过程

本文主角：

${\nabla }_{\theta }J(\theta )\propto {\sum }_{s\in \mathcal{S}}{\mu }^{{\pi }_{\theta }}(s){\sum }_{a\in \mathcal{A}}{Q}^{{\pi }_{\theta }}(s,a){\nabla }_{\theta }{\pi }_{\theta }(a|s)$

这个公式是策略梯度定理的表述，它表明一个策略的性能梯度（即优化目标函数$J(\theta )$的梯度）与在该策略下各状态的访问频率${\mu }^{{\pi }_{\theta }}(s)$，以及在这些状态下，采取不同动作的价值$Q^{{\pi }_{\theta }}(s,a)$和采取这些动作的策略概率的梯度${\nabla }_{\theta }{\pi }_{\theta }(a|s)$的乘积之和成正比。

在强化学习中，这个公式是用来指导如何调整策略参数$\theta$，以便最大化长期奖励。通过梯度上升算法，我们可以改善策略，使得在高价值$Q$​下采取的动作更加频繁，从而提高整体策略的期望回报。

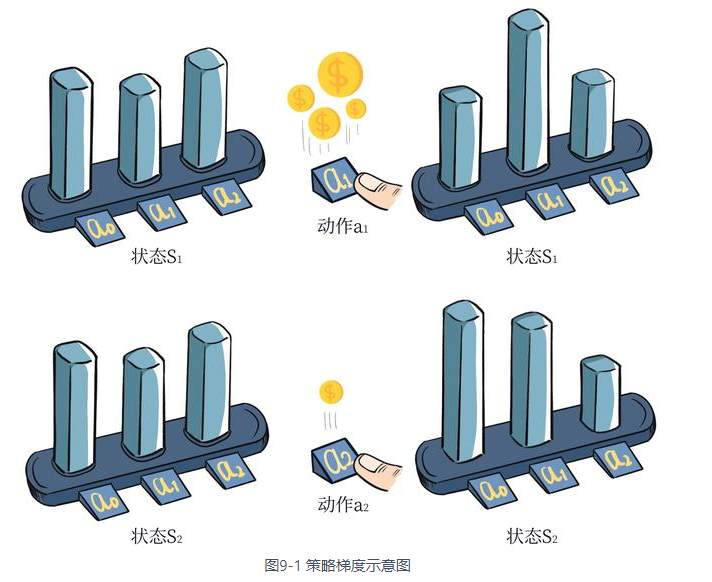
下面是完整推导：

• 定义状态值函数的梯度:
  ${\nabla }_{\theta }{V}^{\pi }(s)={\nabla }_{\theta }\left({\sum }_{a\in A}\pi (a|s)Q^{\pi }(s,a)\right)$
  这一步基于状态值函数$V^{\pi }(s)$的定义，即给定策略$\pi$下，在状态$s$采取所有可能动作$a$的期望回报的总和。这里，$\pi (a|s)$是在状态$s$下选择动作$a$的策略概率，而$Q^{\pi }(s,a)$是执行动作$a$并遵循策略$\pi$的期望回报。

• 应用梯度和乘积规则:
  $={\sum }_{a\in A}\left({\nabla }_{\theta }\pi (a|s)Q^{\pi }(s,a)+\pi (a|s){\nabla }_{\theta }{Q}^{\pi }(s,a)\right)$
  这一步通过应用梯度运算符和乘积规则（$\nabla (xy)=x\nabla y+y\nabla x$）来分解每个项。第一项考虑了策略$\pi (a|s)$对参数$\theta$的直接依赖，而第二项考虑了行为值函数$Q^{\pi }(s,a)$对$\theta$的依赖。

• 行为值函数的梯度展开:
  $={\sum }_{a\in A}\left({\nabla }_{\theta }\pi (a|s)Q^{\pi }(s,a)+\pi (a|s){\nabla }_{\theta }{\sum }_{s^{\prime },r}P(s^{\prime },r|s,a)\left(r+\gamma V^{\pi }(s^{\prime })\right)\right)$
  这里将$Q^{\pi }(s,a)$按其定义展开，即为给定状态$s$和动作$a$后的即时奖励$r$加上折扣后的未来奖励的期望值。梯度作用于整个表达式，注意到$r$和$\gamma$是常数，梯度只作用于$V^{\pi }(s^{\prime })$。

• 简化即时奖励的影响:
  $={\sum }_{a\in A}\left({\nabla }_{\theta }\pi (a|s)Q^{\pi }(s,a)+\gamma \pi (a|s){\sum }_{s^{\prime },r}P(s^{\prime },r|s,a){\nabla }_{\theta }{V}^{\pi }(s^{\prime })\right)$
  在这一步中，即时奖励$r$被省略，因为它不依赖于$\theta$，因此其梯度为零。只有未来奖励的部分，即$\gamma V^{\pi }(s^{\prime })$，对$\theta$有依赖，因此梯度只作用于这部分。

• 进一步简化概率项:
  $={\sum }_{a\in A}\left({\nabla }_{\theta }\pi (a|s)Q^{\pi }(s,a)+\gamma \pi (a|s){\sum }_{s^{\prime }}P(s^{\prime }|s,a){\nabla }_{\theta }{V}^{\pi }(s^{\prime })\right)$​

---

• 从策略梯度的定义开始:
  ${\nabla }_{\theta }{V}^{\pi }(s)=\varphi (s)+\gamma {\sum }_a\pi (a|s){\sum }_{s^{\prime }}P(s^{\prime }|s,a){\nabla }_{\theta }{V}^{\pi }(s^{\prime })$
  这里，$\varphi (s)={\sum }_{a\in A}{\nabla }_{\theta }{\pi }_{\theta }(a|s)Q^{{\pi }_{\theta }}(s,a)$代表了状态$s$的特征向量，它是策略梯度的一部分。接着，考虑了在当前策略下，从状态$s$采取动作$a$转移到状态$s^{\prime }$的概率，以及从状态$s^{\prime }$开始并遵循策略$\pi$​的状态值函数的梯度。
• 展开状态值函数的梯度:
  ${\nabla }_{\theta }{V}^{\pi }(s)=\varphi (s)+\gamma {\sum }_{s^{\prime }}{d}^{\pi }(s\to s^{\prime },1){\nabla }_{\theta }{V}^{\pi }(s^{\prime })$
  $d^{\pi }(s\to s^{\prime },1)$表示在一步转移中从状态$s$到状态$s^{\prime }$的折扣后的状态转移概率。它是一个概率分布，考虑了所有可能的动作。
• 递归地展开状态值函数的梯度:
  ${\nabla }_{\theta }{V}^{\pi }(s)=\varphi (s)+\gamma {\sum }_{s^{\prime }}{d}^{\pi }(s\to s^{\prime },1)\varphi (s^{\prime })+{\gamma }^2{\sum }_{s^{\prime \prime }}{d}^{\pi }(s\to s^{\prime \prime },2){\nabla }_{\theta }{V}^{\pi }(s^{\prime \prime })$
  这一步递归地应用了上一步的逻辑，但这次是对两步转移后的状态$s^{\prime \prime }$。这表明每一步都会增加一个更深层次的期望和一个更高的折扣因子$\gamma$。
• 继续无限递归:
  ${\nabla }_{\theta }{V}^{\pi }(s)=\varphi (s)+\gamma {\sum }_{s^{\prime }}{d}^{\pi }(s\to s^{\prime },1)\varphi (s^{\prime })+{\gamma }^2{\sum }_{s^{\prime \prime }}{d}^{\pi }(s\to s^{\prime \prime },2)\varphi (s^{\prime \prime })+\dots$
  推导继续进行，考虑到所有可能的未来状态和它们对应的特征向量，乘以它们的转移概率和适当的折扣因子。
• 总结为无限和:
  ${\nabla }_{\theta }{V}^{\pi }(s)={\sum }_{x\in S}{\sum }_{k=0}^{\infty }{\gamma }^k{d}^{\pi }(s\to x,k)\varphi (x)$
  最后一步是将所有无限递归的项总结为一个无限序列和。这里$d^{\pi }(s\to x,k)$是从状态$s$到状态$x$在$k$​步内的折扣后的转移概率。这个无限和形式的期望值是对状态值函数的梯度的完整描述。

---

• 目标函数的梯度:
  ${\nabla }_{\theta }J(\theta )={\nabla }_{\theta }{\mathbb{E}}_{s_0}[V^{{\pi }_{\theta }}(s_0)]$
  这一步定义了目标函数$J(\theta )$作为初始状态$s_0$下的状态值函数$V^{{\pi }_{\theta }}(s_0)$的期望值的梯度。

• 引入状态转移概率:
  $={\sum }_s{\mathbb{E}}_{s_0}\left[{\sum }_{k=0}^{\infty }{\gamma }^k{d}^{{\pi }_{\theta }}(s_0\to s,k)\right]\varphi (s)$
  此处，将目标函数中的期望展开，包含从初始状态$s_0$到任意状态$s$的折扣转移概率$d^{{\pi }_{\theta }}(s_0\to s,k)$，乘以状态$s$的特征向量$\varphi (s)$。每个状态的特征向量与它被访问的概率加权求和。

• 引入状态分布$\eta (s)$:
  $={\sum }_s\eta (s)\varphi (s)$
  这里，$\eta (s)$是在策略${\pi }_{\theta }$下访问状态$s$的稳态分布。它是从任何初始状态出发，经过无限步骤后到达状态$s$的概率。

• 状态分布的规范化:
  $\propto {\sum }_s\frac{\eta (s)}{{\sum }_{s^{\prime }}\eta (s^{\prime })}\varphi (s)$
  这一步表明状态分布被规范化了，使得所有状态的分布之和为1。这是为了将状态分布转化为概率分布。

• 使用$\eta (s)$的定义:
  $={\sum }_s\mu (s){\sum }_a{Q}^{{\pi }_{\theta }}(s,a){\nabla }_{\theta }{\pi }_{\theta }(a|s)$
  最终，我们得到了策略梯度定理的标准形式。这里$\mu (s)$代表状态$s$在策略${\pi }_{\theta }$下的访问频率，而$Q^{{\pi }_{\theta }}(s,a)$是在状态$s$下采取动作$a$的行为值函数。梯度${\nabla }_{\theta }{\pi }_{\theta }(a|s)$表示策略对参数的依赖性。